7.5. Изоморфизм евклидовых пространств

Определение 52. Два евклидовых пространства Е и Е¹ называются изоморфными, если они изоморфны как линейные пространства и для любых двух пар соответствующих векторов а, а¹ и в, в¹ выполняется равенство (а, в) = (а¹, в¹).

Теорема 47. Два конечномерных евклидова пространства Е и Е¹ изоморфны тогда и только тогда, когда dim E = dim E ¹.

Доказательство.  Пусть Е и Е¹ изоморфны. Тогда они изоморфны и как линейные пространства. Из свойств изоморфизма линейных пространств следует, что dim E = dim E ¹.

 Пусть dim E = dim E ¹ = n. Выберем в пространствах Е и Е¹ ортонормированные базисы е = (е₁, е₂, ... , е_n) и е¹ = (е₁¹, е₂¹, ... , е_n¹) соответственно. Зададим отображение : Е  Е¹ по следующему правилу. Если а  Е и а = х₁е₁ + х₂е₂ + … + х_nе_n, то пусть (а) = х₁е₁¹ + х₂е₂¹ + … + х_nе_n¹. Это отображение является, очевидно, изоморфизмом между линейными пространствами Е и Е¹. Покажем, что при этом отображении сохраняется скалярное произведение векторов. Пусть в  Е и в = у₁е₁+ у₂е₂ + … + у_nе_{n .} Тогда  (в) =у₁е₁¹+ у₂е₂¹ + … + у_nе_n¹_. Так как базис е ортонормированный, то (а,в)= х₁у₁ + х₂у₂ +…+ х_nу_n. Так как базис е¹ ортонормированный, то ((а), (в)) = х₁у₁ + х₂у₂ + … + х_nу_n. Следовательно, (а,в) = ((а), (в)). Итак,  - изоморфизм между Е и Е¹.

Следствие. Если на конечномерном линейном пространстве различными способами задавать скалярные произведения, то все получающиеся при этом евклидовы пространства будут изоморфными.

VIII. Некоторые виды линейных преобразований евклидовых пространств

Так как евклидовы пространства являются линейными пространствами, то все свойства линейных преобразований линейных пространств верны и в евклидовых пространствах. Но все эти свойства связаны лишь с двумя алгебраическими операциями: сложением векторов и умножением вектора на элемент поля Р. В евклидовом пространстве есть ещё одна операция: скалярное умножение векторов. В зависимости от того как меняется скалярное произведение выделяются некоторые частные виды линейных преобразований.

8.1. Ортогональные линейные преобразования

Определение 53. Линейное преобразование  евклидова пространства Е называется ортогональным, если для любых векторов а и в из Е выполняется условие (а, в) = ((а), (в)). (49)

Свойства ортогональных преобразований.

Пусть  – ортогональное преобразование пространства Е.

1⁰. | а| = |(а)| для любого вектора а.

| а| = = = | (а)|.

2⁰. = для любых векторов а и .

3⁰. Пусть Е_n конечномерное евклидово пространство, е = (е₁, е₂, ... , е_n) – базис в нём, А – матрица преобразования  и Г – матрица Грама в этом базисе. Тогда (а) = Ах, ( ) = Ау, где х и у –столбцы координат векторов а и соответственно; (а, ) = х^ТГу, ((а), ( )) = (Ах)^ТГ( Ау) = х^Т(А^ТГА)у. Так как (а, ) = ((а), ( )), то Г = А^ТГА. Итак, матрица ортогонального преобразования удовлетворяет условию

Г = А^ТГА (50)

Справедливо и обратное. Если в Е_n зафиксирован базис и Г – матрица Грама в этом базисе, то матрица А, удовлетворяющая условию (48), задаёт ортогональное преобразование.

Если базис е = (е₁, е₂, ... , е_n) ортонормированный, то Г = Е и формула (50) примет вид

А^Т А = Е, или А^Т = А^–1.

Определение 54. Квадратная матрица А называется ортогональной, если

А^Т = А^–1 (51).

Теорема 48. Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда в ортонормированном базисе оно задаётся ортогональной матрицей.

Доказательство следует из свойства 3⁰ и определения 53.

Теорема 49. Квадратная матрица является ортогональной тогда и только тогда, когда сумма квадратов всех элементов любого столбца (или строки) равна 1, а сумма попарных произведений соответствующих элементов двух различных столбцов (или строк) равна нулю.

Доказательство следует из формулы 51.

Теорема 50. Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда оно ортонормированный базис переводит в ортонормированный базис.

Доказательство.  Пусть  : Е_n  Е_n ортогональное преобразование и пусть е = (е₁, е₂, ... , е_n) ортонормированный базис в Е_n . Если А – матрица этого преобразования в базисе е, то А – ортогональная. Но тогда (е) = еА. Распишем это равенство, если

А = .

Получим (ек) = а1ке1 + а2ке2 + … + аnкеn . Так как базис е ортонормированный, то ((ек))2 = 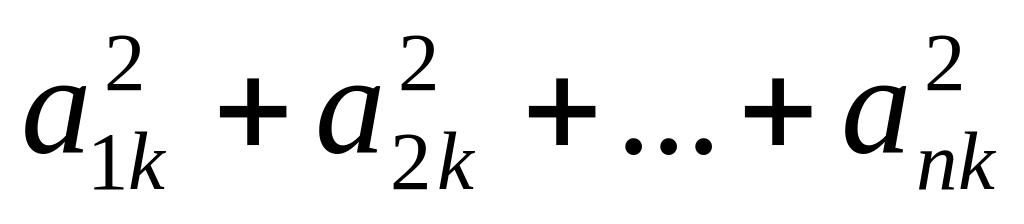= (ек)2 = 1, т.е. все векторы (ек) единичной длины. По той же причине ((ек), (ер)) = а1ка1р + а2ка2р + … + аnкаnр = (ек , ер ) = 0,

если к  р, т.е. (е_к)  (е_р). Так как векторы системы (е) попарно ортогональны, то они линейно независимы, т.е. (е) – базис. Итак, (е) – ортонормированный базис.

 Пусть е и (е) – ортонормированные базисы. Тогда 1 = ((е_к))² = и 0 = ((е_к), (е_р)) = а_1ка_1р + а_2ка_2р + … + а_nка_nр при к  р. Следовательно, по теореме 49, матрица А – ортогональная.

Теорема 51. Если матрица А ортогональная, то |А | =  1.

Действительно, если матрица А ортогональная, то А^Т А = Е. Отсюда |А^ТА | = |Е |, |А^Т|| А| = 1, |А||А| = 1, |А|² = 1, |А| = 1.

Теорема 52. Собственные значения ортогонального преобразования могут быть только 1 или (–1).

Доказательство. Пусть  – собственное значение ортогонального преобразования .

Тогда существует такой ненулевой вектор (х₁, х₂, … , х_n )^Т, что Ах = х, где А – матрица преобразования . Равенство транспонируем и перейдём к сопряжённым числам, получим . Перемножим почленно оба равенства. . Так как А – действительная ортогональная матрица, то . Следовательно, . Отсюда , т.е. ||² = 1. Но это и значит, что собственными значениями могут быть только числа 1 и (–1).

Теорема53. Собственные векторы ортогонального преобразования, принадлежащие различным собственным значениям ортогональны.

Доказательство. Для любых а и в из Е_n имеет место (а, в) = ((а), (в)) = (₁а, ₂в) = = ₁₂(а, в). Так как ₁  ₂, то, согласно предыдущей теоремы, ₁ =1, ₂ = –1. Следовательно, (а, в) = – (а, в). Отсюда (а, в) = 0. Так как а и в не нулевые, то они ортогональные.