3. Энтропия в термодинамике

Для цикла Карно справедливо равенство (учтём, что )

или

Любой обратимый цикл можно представить как бесконечное число бесконечно узких циклов Карно и записать для него уравнение Клаузиуса . Интеграл Клаузиуса .

Существует функция состояния – энтропия, дифференциал которой равен приведённой теплоте .

4. Основные свойства энтропии:

1. Для кругового обратимого цикла и S = 0.

2. Для обратимого процесса изменение энтропии не зависит от процесса, а определяется начальным и конечным состояниями (как и для внутренней энергии U) .

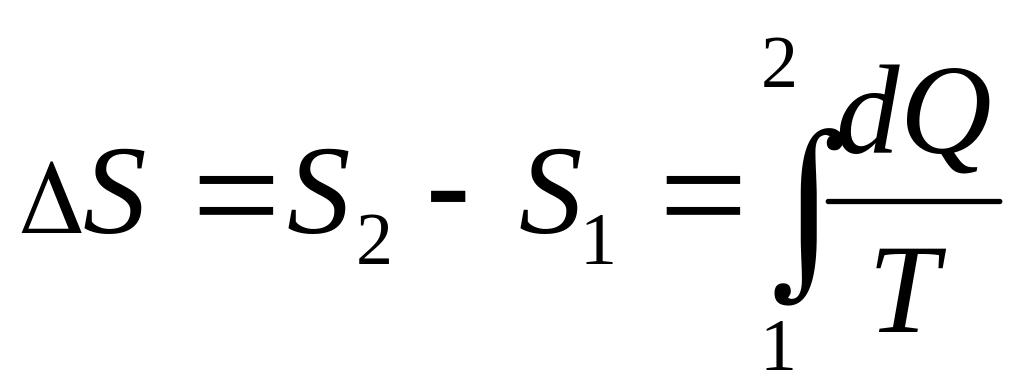3. Если же цикл включает в себя необратимый процесс и оказывается необратимым, то уравнение не выполняется и имеет место неравенство Клаузиуса

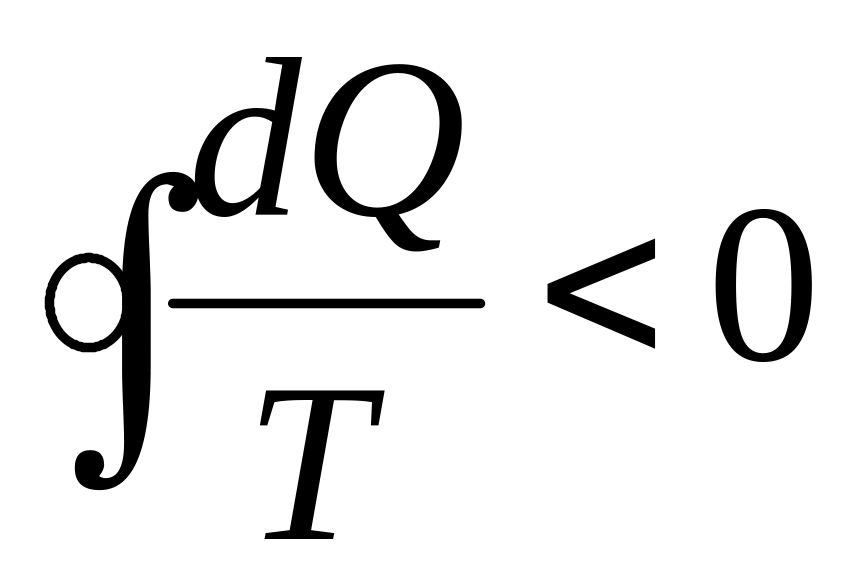   , что легко доказать из

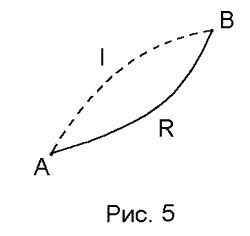4. Р ассмотрим цикл, в котором один процесс необратимый (АIB), а второй обратимый (ARB).

Изменение энтропии при переходе из состояния A в B по обратимому процессу .

Чтобы определить изменение энтропии для необратимого процесса, рассмотрим необратимый цикл AIBRA, состоящий из необратимого процесса I от A до B и обратимого процесса R от B до A.

Применяя неравенство Клаузиуса к этому циклу, имеем:

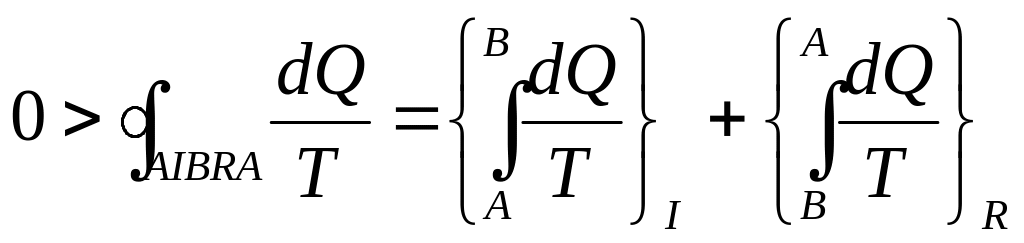
Для обратимого процесса (BRA): . Используем это и получим неравенство

где интеграл берется по произвольному необратимому процессу I от A до B. Т.е. изменение энтропии в необратимом процессе больше приведённой теплоты – имеет место производство энтропии за счёт неравновесности процесса!

5. Закон возрастания энтропии

Применим последнее неравенство к изолированной системе, которая никак не взаимодействует с окружающей средой. Поскольку для такой системы δ Q = 0, то получаем

Для любого процесса в изолированной системе энтропия конечного состояния не может быть меньше энтропии начального состояния. Это – закон возрастания энтропии.

Если процесс обратим, то при достижении максимального значения в состоянии равновесия энтропия системы не меняется .

Закон возрастания энтропии справедлив только для изолированных систем. С помощью внешней системы можно уменьшить энтропию тела. Однако суммарная энтропия тела и внешней системы уменьшиться не может.

Если изолированная система находится в состоянии с максимальной энтропией, соответствующей её энергии, то в ней не могут происходить никакие процессы, поскольку любой процесс привел бы к уменьшению энтропии.

Таким образом, состояние с максимальной энтропией является наиболее устойчивым состоянием изолированной системы.

Самопроизвольные процессы в изолированных системах идут в направлении роста энтропии. Примеры.

1. Рассмотрим теплообмен между двумя частями системы A₁ и A₂, имеющими температуры T₁ и T₂. Пусть T₁<T₂. Теплота передается от горячего тела к холодному. Поэтому тело A₂ передаст телу A₁ некоторое количество теплоты Q, т.е.

Δ Q1 = Q ,              Δ Q2 = –Q .

При этом энтропия тела A₁ изменится на величину Δ Q₁/T₁ , а энтропия тела A₂ – на величину Δ Q₂/T₂ . Общее изменение энтропии системы

(46)

Поскольку T₁<T₂ , то Δ S>0 .

2. Рассмотрим теперь выделение теплоты при трении. Энтропия тела, которое нагревается при трении, возрастает. Это увеличение энтропии не компенсируется уменьшением энтропии других частей системы, так как теплота получена из работы.