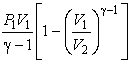Первый закон (начало) термодинамики

– есть закон сохранения энергии для термодинамических систем:

При переходе системы из состояния A в состояние B сумма работы и теплоты, полученных системой от окружающей среды, определяется только состояниями A и B; эта сумма не зависит от того, каким способом осуществляется переход из A в B.

∆U = Q – A .

Величина U называется внутренней энергией системы. В феноменологической термодинамике этот закон постулирует существование функции состояния U.

Для бесконечно малого изменения состояния

dU = δ Q – δ A ,

или

δ Q= dU + PdV .

Величины Q и A не являются функциями состояния системы; они зависят от способа перехода из состояния 1 в 2. Соответственно этому δ Q и δ L не являются полными дифференциалами. Следует различать работу газа и работу внешних сил: A_газа= – A^

Теплоемкость – есть функция процесса Различают теплоемкость при постоянном V , следовательно и теплоемкость при постоянном p

Второй член в формуле для c_P связан со слагаемым PdV, т.е. описывает эффект, оказываемый на теплоемкость работой, которую система совершает во время расширения.

Уравнение Майера легко получить, используя уравнение состояния для идеального газа PV = RT : .

Применение I-го закона к газовым процессам

Изотермический ; ; – гипербола.

Изохорический ; ; .

Изобарический ; .

Адиабатический ; ; .

Вывод уравнения адиабаты.

; ;

; или ;

Политропические процессы – изопроцессы идущие при постоянной теплоемкости : – общий случай изопроцессов.

;

Работа 1-го моля газа в политропических процессах

, используя ,

получаем .

При n = 1 – изотерма .

Частные изопроцессы

     

Термодинамический процесс	Показатель политропы	Теплоемкость	Работа
Изотермический	1
Изобарический	0
Изохорический			0
Адиабатический		0

Процессы с отрицательной теплоёмкостью (?) Найти и построить! Исходить из соотношения

Второй закон термодинамики

Введение

Первое начало термодинамики, выражая закон cохранения и превращения энергии, не позволяет уcтановить направление протекания термодинамических процеccов. Кроме того, существует множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются. Появление второго начала термодинамики прежде всего связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие нет. Второе начало термодинамики задает направление протекания термодинамических процессов.

Используя понятие энтропии и связанное с ним неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы возрастает.

Можно дать более короткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Существенен момент, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя произвольным образом (возрастать, убывать, оставаться постоянной). Кроме того, повторим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах и в замкнутой системе энтропия всегда возрастает.

Формула Больцмана S=k•lnW дает объяснение постулируемое вторым началом термодинамики возрастанию энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Значит, формула Больцмана дает статистическое толкование второго начала термодинамики. Являясь статистическим законом, оно описывает закономерности хаотического движения огромного числа частиц, которые составляющих замкнутую систему.

Дадим еще две формулировки второго начала термодинамики: 1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Можно довольно просто доказать эквивалентность формулировок Кельвина и Клаузиуса. Более того, показано, что если в замкнутой системе провести воображаемый процесс, который противоречит второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это же доказывает эквивалентность формулировки Клаузиуса (а значит, и Кельвина) и статистической формулировки, по которой энтропия замкнутой системы не может убывать. В середине XIX в. возникла проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему и применяя к ней второе качало термодинамики, Клаузиус пришел к утверждению, что энтропия Вселенной когда-нибудь достигнет своего максимума. Это означает, что все формы движения со временем должны перейти в тепловую. При этом переход теплоты от горячих тел к холодным приведет к тому, что температура всех тел во Вселенной станет одинаковой, т. е. наступит полное тепловое равновесие и все процессы во Вселенной остановятся — наступит тепловая смерть Вселенной. Неправильность вывода о тепловой смерти заключается в том, что не имеет смысла применять второе начало термодинамики к незамкнутым системам, например к такой бесконечно развивающейся и безграничной системе, как Вселенная. Первые два начала термодинамики дают мало сведений о поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом термодинамики, или теоремой Нернста—Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

Так как энтропия задается с точностью до аддитивной постоянной, то эту постоянную для простоты возьмем равной нулю. При этом отметим, что это произвольное допущение, т.к. энтропия по своей сущности всегда задается с точностью до аддитивной постоянной. Из теоремы Нернста — Планка следует, что теплоемкости С_р и С_V при 0 К равны нулю.

Тепловой двигатель – устройство, способное превращать теплоту в механическую работу в процессе расширения рабочего тела. В качестве рабочего тела обычно используются газообразные вещества (воздух, водяной пар и др.)

Э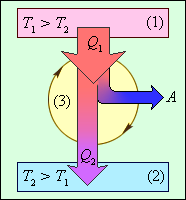 нергетическая схема тепловой машины :

1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1 > 0, A > 0, Q2 < 0; T1 > T2.

Общее выражение для КПД

В применяемых в технике двигателях используются различные круговые процессы. Рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный КПД карбюраторного двигателя ~ 30%, у дизельного двигателя ~ 40 %.

1. Цикл Карно.

КПД обратимой тепловой машины

В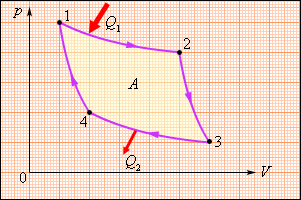 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат – цикл Карно.   Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, то есть бесконечно близким к состоянию теплового равновесия с окружающими телами (тепловыми резервуарами или термостатами). Цикл Карно исключает теплообмен при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника: (доказательство потом).

2. КПД цикла Карно ;

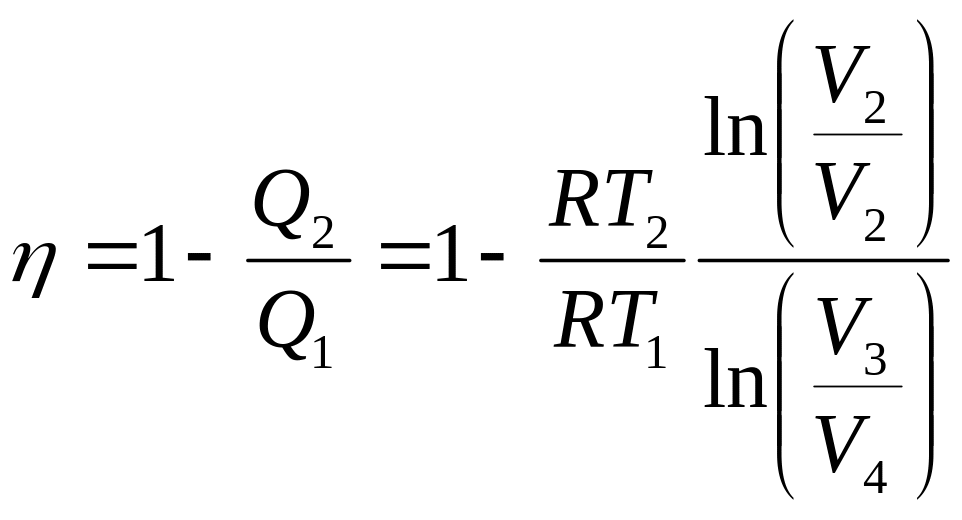Из уравнения адиабаты следует и

И далее . Следовательно . Это получил и сам Карно.