84.Прямое и обратное преобразования Фурье.
Периодическая
функция времени, подчиняющаяся условиям
Дирихле(Функция
– есть функция, ограниченной вариации
на каждом конечном интервале
,
на котором она ограничена и имеет
конечное число относительных максимумов
и минимумов и точек разрыва первого
рода), может быть разложена в ряд Фурье.
,
где k
– порядок гармоники,
–
основная гармоника процесса.
, , - коэффициенты Фурье
=
+
=
+
+
=
Подставим значения , , :
Введем обозначения:
)
, e
→1
) - частотный спектр сигнала в комплексном виде
x(t)
x(t) – обратное преобразование Фурье (временной сигнал в частотный спектр)
Этот ряд в комплексной форме имеет вид:
, k=±1, ±2,
±3, ...
x(t)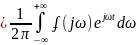
- обратное преобразование Фурье
-
прямое преобразование Фурье
Таким образом,
Периодическая функция времени может быть представлена совокупностью дискретных гармоник с интервалом по частоте между гармониками, равным основной частоте
.
Непериодическая
функция времени может рассматриваться
как периодическая с периодом,
стремящимся к бесконечности. В этом
случае вместо приведённых выше формул
получаются два интегральных уравнения
Фурье, связывающих оригинал
и её частотное изображение (преобразование
Фурье). В отличие от разложения в ряд
Фурье здесь получается разложение в
непрерывный спектр частот с интервалом
по частоте между гармониками, равными
бесконечно малой величине
.
Недостатком интеграла Фурье является то, что он принадлежит к числу несобственных интегралов и может применяться для так называемых абсолютно интегрируемых функций времени (т. е. Удовлетворяющих неравенству
.)
85.Прямое и обратное преобразования Фурье.
Периодическая функция времени, подчиняющаяся условиям Дирихле(Функция – есть функция, ограниченной вариации на каждом конечном интервале , на котором она ограничена и имеет конечное число относительных максимумов и минимумов и точек разрыва первого рода), может быть разложена в ряд Фурье.
,
где k – порядок гармоники, – основная гармоника процесса.
, , - коэффициенты Фурье
= + = +
+ =
Подставим значения , , :
Введем обозначения:
) , e →1
) - частотный спектр сигнала в комплексном виде
x(t)
X(t) – обратное преобразование Фурье (временной сигнал в частотный спектр)
Этот ряд в комплексной форме имеет вид:
, k=±1, ±2, ±3, ...
X(t) - обратное преобразование Фурье
- прямое преобразование Фурье
Таким образом,
Периодическая функция времени может быть представлена совокупностью дискретных гармоник с интервалом по частоте между гармониками, равным основной частоте .
Непериодическая функция времени может рассматриваться как периодическая с периодом, стремящимся к бесконечности. В этом случае вместо приведённых выше формул получаются два интегральных уравнения Фурье, связывающих оригинал и её частотное изображение (преобразование Фурье). В отличие от разложения в ряд Фурье здесь получается разложение в непрерывный спектр частот с интервалом по частоте между гармониками, равными бесконечно малой величине .
Недостатком интеграла Фурье является то, что он принадлежит к числу несобственных интегралов и может применяться для так называемых абсолютно интегрируемых функций времени (т. е. Удовлетворяющих неравенству .)
86.Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии, и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть, обратимый переход от временно́го пространства (time domain) в частотное пространство (frequency domain). Богатые возможности применения основываются на нескольких полезных свойствах преобразования:
Преобразования обратимы, причём обратное преобразование имеет практически такую же форму, как и прямое преобразование.
Синусоидальные базисные функции (вернее, комплексные экспоненты) являются собственными функциями дифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические. (Например, в линейной стационарной системе частота — консервативная величина, поэтому поведение на каждой частоте может решаться независимо.)
По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.
Дискретная версия преобразования Фурье может быстро рассчитываться на компьютерах, используя алгоритм быстрого преобразования Фурье
Можно только перечислить несколько областей: анализ сигналов, фильтрация, ускоренное вычисление корелляции и свертки, использование в алгоритмах быстрого умножения чисел, и во многих других случаях оно также находит свое применение.