7. Дробово-лінійне програмування

7.1 Приклади дробово-лінійних задач

Приклад 7.1.

Сільськогосподарське акціонерне товариство з обмеженою відповідальністю, яке розміщене в Лісостепу України, має намір оптимізувати структуру виробництва. За критерій оптимальності взято максимізацію рентабельності як відношення прибутку до собівартості. Дані про види діяльності, що їх здійснюватиме товариство, наведено в таблиці:

Показник	Діяльність з вирощування							Ресурс
	озимої пшениці, га	цукрових буряків, га	корів продуктивністю, кг				кормових культур, га
			5000	4500	4000	3500
Урожайність, т/га	4	35	—	—	—	—	6	—
Собівартість, грн./т	600	250	600	700	800	9000	200	—
Ціна, грн./т	800	300	1000	1000	1000	1000	—	—
Вихід кормів, тон кормо- вих одиниць/га	0,8	2,0	—	—	—	—	6	—
Витрати живої праці, людино-днів/га	4	25	6	6	6	6	3	26 000
Витрати механізованої праці, людино-днів/га	2	8	3	3	3	3	2	11 000
Частка корів у стаді	—	—	0,1	0,2	0,3	0,4	—
Потреба в кормах, т/гол	—	—	5	4,7	4,4	4,1	—	—

Акціонерне товариство має 2500 га ріллі.

Записати економіко-математичну модель і знайти оптимальну структуру виробництва.

Розв’язання. Введемо позначення:

х₁ — площа посіву озимої пшениці, га;

х₂ — площа посіву цукрового буряка, га;

х₃ — площа посіву кормових культур, га;

х₄ — кількість корів продуктивністю 5000 кг;

х₅ — кількість корів продуктивністю 4500 кг;

х₆ — кількість корів продуктивністю 4000 кг;

х₇ — кількість корів продуктивністю 3500 кг.

Запишемо критерій оптимальності:

за розглянутих далі умов.

1. Обмеження за ресурсами.

1) Ріллі:

.

2) Живої праці:

.

3) Механізованої праці:

.

2. Обмеження сівозміни.

1) Посівна площа кормових має бути більша або дорівнювати площі під озимою пшеницею:

.

2) Посівна площа озимої пшениці має бути більша або дорівнювати площі під цукровими буряками:

.

3. Структура корів за продуктивністю.

1) Балансове рівняння щодо корів:

,

де — загальна кількість корів.

2) Частка корів продуктивністю 5000 кг:

.

3) Частка корів продуктивністю 4500 кг:

.

4) Частка корів продуктивністю 4000 кг:

.

5) Частка корів продуктивністю 3500 кг:

.

4. Забезпеченість корів кормами:

.

Невід’ємність змінних:

.

Щоб знайти розв’язок за цією моделлю, зробимо відповідну заміну й скористаємося симплексним методом:

.

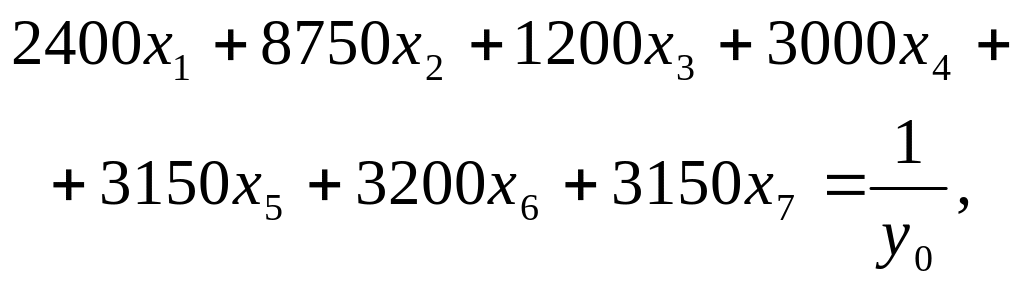
Отже, маємо таку лінійну економіко-математичну модель:

за розглянутих далі умов.

1.  ,

,

.

2.  , або ,

, або .

3.  ,

,

,

,

.

4.  .

5.  .

Приклад 7.2.

Розв’язати графічно задачу дробово-лінійного програмування:

за умов

Розв’язання. Побудуємо на площині область допустимих роз­в’язків задачі — трикутник АВС.

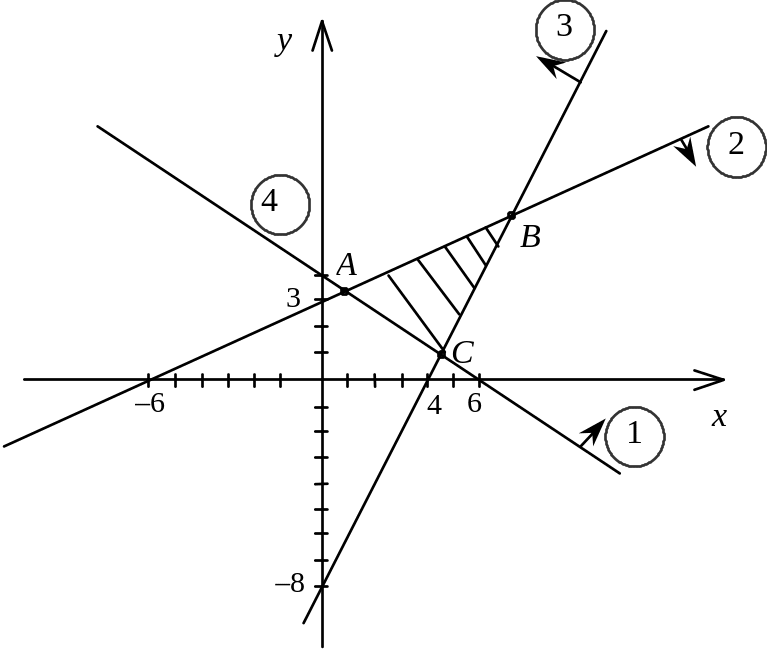
Цільова функція задачі являє собою пряму, яка обертатиметься навколо початку системи координат залежно від змінюваних параметрів х₁, х₂ так, що точки А і С будуть точками максимуму і мінімуму функції. Виразимо х₂ із цільової функції:

.

Кутовий коефіцієнт цільової функції

.

Розглянемо похідну

.

Оскільки при будь-якому значенні Z вона від’ємна, то функція R_Z є спадною (зі зростанням Z кутовий коефіцієнт R_Z зменшується), а графік цільової функції обертатиметься навколо початку координат за годинниковою стрілкою. Отже, точка С є точкою максимуму, а точка А — мінімуму досліджуваної задачі.

Знайдемо координати цих точок.

Точка А:

Звідси

Точка А має координати (6/7; 24/7).

Точка С:

Звідси

Точка С має координати (9/2; 1).

Знайдемо значення цільової функції в цих точках:

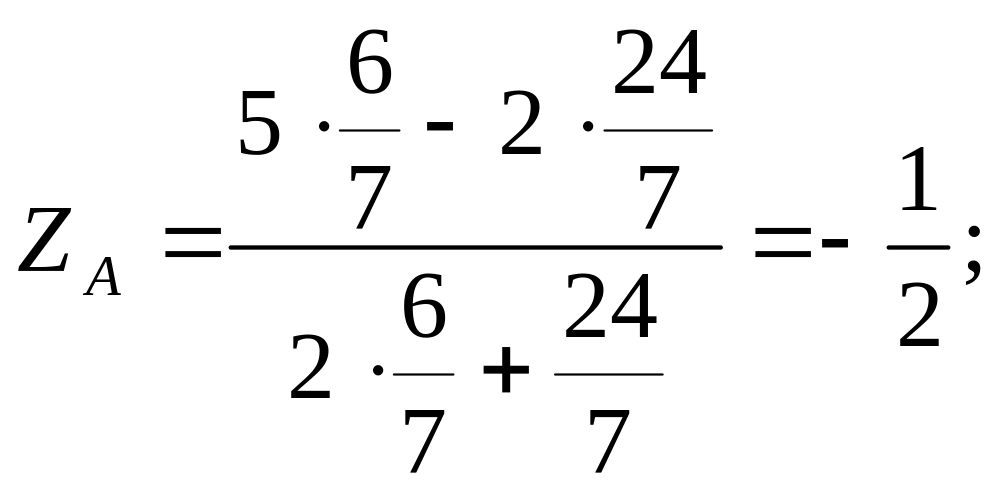
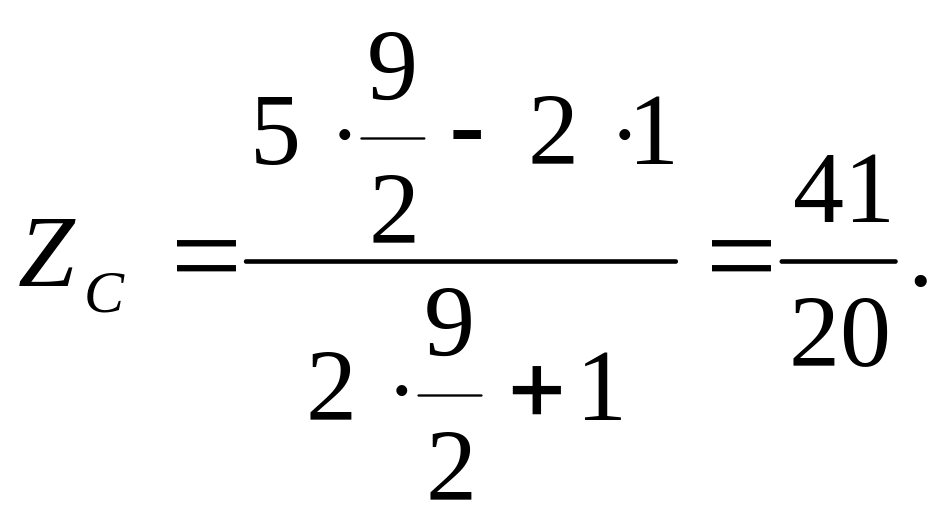
Результати (Z_C > Z_A) підтверджують, що оптимуми знайдено правильно: максимум досягається в точці С, а мінімум — у точці А.

Приклад 7.3.

Розв’язати задачу дробово-лінійного програмування симплексним методом:

за умов

Розв’язування. Зведемо початкову задачу до задачі лінійного програмування згідно з розглянутими раніше правилами.

Позначимо .

Введемо нові змінні:

, .

Дістанемо задачу лінійного програмування:

за умов

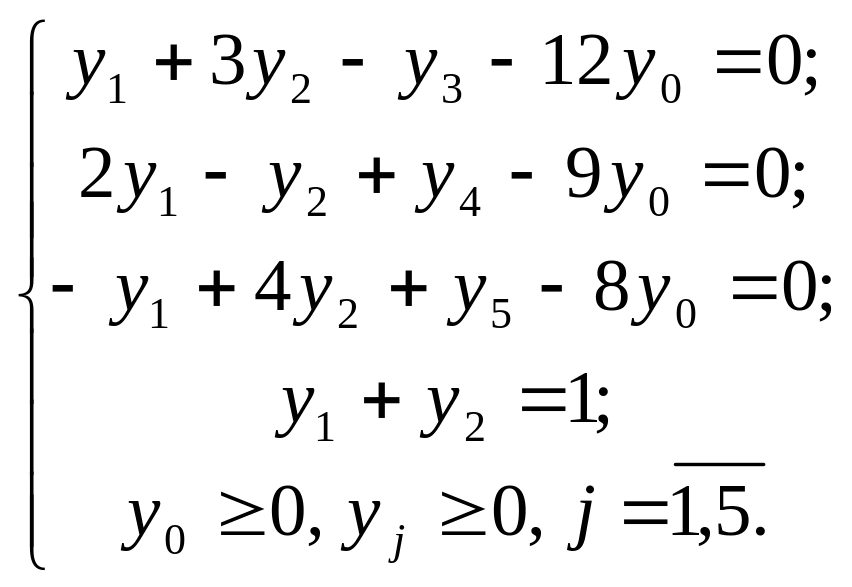
Розв’яжемо задачу симплексним методом. У перше та останнє обмеження введемо штучні змінні y₆, та y₇.

Маємо оптимальний розв’язок перетвореної задачі:

, , , .

Знайдемо оптимальний розв’язок початкової задачі, враховуючи, що :

; ; ;

; .

Отже, ,

.