
- •Содержание
- •1 Предмет, цели и задачи идентификации, области применения
- •2 Проблемы точности, критерии и условия
- •6.2 Методика идентификации моделей объектов
- •6.3 Методика идентификации моделей объектов
- •6.4 Методика идентификации моделей объектов
- •8 Идентификация параметров объекта во временной и
- •10 Применение идентификации в системах
- •1 Предмет, цели и задачи идентификации, области применения
- •1.1 Сущность идентификации, ее цели и задачи
- •1.2 Проблемы выбора модели объекта идентификации
- •1.3 Области применения идентификации
- •2 Проблемы точности, критерии и условия идентификации
- •2.1 Анализ ошибок, возникающих в системе идентификации
- •2.2 Критерии идентификации
- •2.3 Управляемость, наблюдаемость и идентифицируемость объекта
- •3 Основные типы моделей в теории идентификации
- •3.1 Модели для описания непрерывных систем
- •3.2 Модели для описания дискретных систем
- •3.3 Основные типы сигналов
- •4 Методы идентификации моделей объектов типовых звеньев по временным и частотным характеристикам
- •4.1. Математическая обработка динамическиххарактеристик объектов управления
- •4.2 Идентификация параметров модели апериодического звена 1-го порядка по временным характеристикам
- •4.3 Идентификация моделей в виде апериодических звеньев II-го порядка
- •4.4 Идентификация моделей в виде передаточной функции колебательного звена II-го порядка по временным характеристикам
- •4.5 Идентификация моделей в виде типовых динамическихзвеньев по частотным характеристикам
- •5Методика идентификации моделей в виде передаточной функции по кривым разгона на основе метода площадей (метод симою)
- •6 Методика идентификации моделей объектов III-го порядка по их временным характеристикам
- •6.1 Типы моделей
- •6.2 Методика идентификации моделей объектов III-го порядка первого типа по их временным характеристикам
- •6.3 Методика идентификации моделей объектов III-го порядка второго типа по их временным характеристикам
- •6.4 Методика идентификации моделей объектов III-го порядка третьего типа по их временным характеристикам
- •7 Анализ динамики и параметров идентификации с учетом объекта
- •7.1 Модель исполнительной части следящей системы
- •7.2 Анализ жесткого объекта при изменении момента инерции нагрузки
- •7.3 Анализ объекта с упругой механической передачей
- •8 Идентификация параметров объекта во временной и частотной области
- •8.1 Обоснование идентифицируемости объекта
- •8.2 Идентификация параметров объекта по переходной функции (методика Орманса)
- •8.3Оценка коэффициентов передаточной функции с помощью гармонических входных воздействий
- •8.4 Идентификация параметров объекта с помощью квадрата модуля частотной характеристики и метода наименьших квадратов
- •8.5Идентификация параметров объекта с применением квадрата модуля обратной частотной характеристики
- •9 Статистические методы анализа, идентификации и моделирования
- •9.1 Условия применения методов статистического анализа
- •9.2 Спектральный анализ входных периодических сигналов
- •9.3 Особенности спектрального анализа методом бпф.
- •9.4 Спектральный анализ сигналов в виде непериодической функции
- •9.5 Статистический анализ с применением сигналов белого шума
- •9.6 Статистический анализ реализации случайного процесса на выходе системы
- •9.7 Статистические методы построения модели и идентификации параметров
- •10 Применение идентификации в системах адаптивного управления
- •10.1 Основные схемы контуров адаптации и функции систем идентификации
- •10.2 Определение параметров эталонной модели и передаточной функции устройства адаптации.
- •10.3 Разработка алгоритма и структурной схемы адаптивной настройки регулятора
- •Литература
- •44/2010. Підп. До друку . Формат 60 х 84/8.
- •84313, М. Краматорськ, вул. Шкадінова, 72.
5Методика идентификации моделей в виде передаточной функции по кривым разгона на основе метода площадей (метод симою)
Для расчета и построения системы автоматического управления технологическим объектом необходимо знать его математическую модель. В инженерной практике в качестве моделей технологических объектов чаще используют передаточные функции. Передаточная функция конкретного объекта управления находится, как правило, из кривой разгона (графика переходного процесса). Кривая разгона, представляющая собой график изменения выходной (регулируемой) величины во времени при подаче на вход объекта ступенчатого воздействия, может быть легко определена опытным путем.
Рассмотренные выше методы идентификации параметров объекта управления являются приближенными. Для более точной идентификации параметров объекта используют метод М.П. Симою, или «метод площадей», который позволяет определить параметры передаточной функции по кривой разгона объекта. Этот метод является одним из наиболее эффективных и удобных для реализации на ЭВМ.
При подаче на вход
объекта ступенчатого возмущения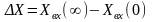 выходная величина
выходная величина
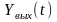 будет изменяться с течением времени
плавно и изменяться на величину
будет изменяться с течением времени
плавно и изменяться на величину
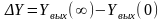 (см. рис. 5.1). Здесь
(см. рис. 5.1). Здесь
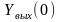 и
и
 – начальные значения соответственно
выходной и входной величин,
– начальные значения соответственно
выходной и входной величин,
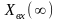 и
и
 – установившиеся (конечные) значения
этих величин.
– установившиеся (конечные) значения
этих величин.
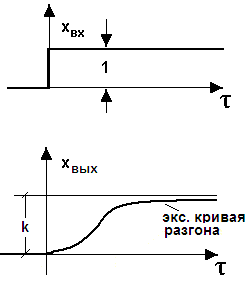
Рисунок 5.1 – Экспериментальная кривая разгона апериодического звена второго порядка.
В основу метода положено предположение, что исследуемый объект может быть описан безразмерной передаточной функцией с постоянными коэффициентами а1, а2, … , аn, b1, b2, … , bnпредставленной в следующем виде
 ,n>m (5.1)
,n>m (5.1)
При использовании этого метода исходную экспериментальную кривую разгона перестраивают в координатах вых(), т.е. осуществляется приведение к единице выходной и входной величины в безразмерном виде:
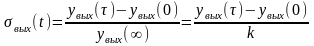 , (5.2)
, (5.2)
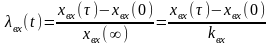 . (5.3)
. (5.3)
В результате перестроения и получают исходную характеристику в диапазоне [0,1] как изображено на рис. 5.2
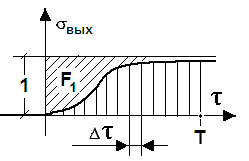
Рисунок5.2 – Преобразование экспериментальной кривой разгона апериодического звена второго порядка при использовании метода Симаю.
Обычно полином A(p) ограничивают 3-им порядком:
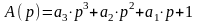 . (5.4)
. (5.4)
Рассмотрим частные случаи.
1) Если хвых=0 при =0, то полином B(p) будет 2-го порядка и, следовательно,
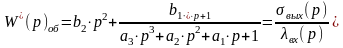 . (5.5)
. (5.5)
2)
Если хвых=0
при =0
и
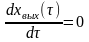 при =0,
что имеет место для данной экспериментальной
кривой разгона, то полином B(p)
будет 1-го порядка, а искомая математическая
модель имеет вид:
при =0,
что имеет место для данной экспериментальной
кривой разгона, то полином B(p)
будет 1-го порядка, а искомая математическая
модель имеет вид:
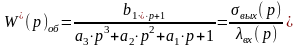 . (5.6)
. (5.6)
Для решения этой задачи кривую разгона, перестроенную в координатах вых()на отрезке (0tуст) разбивают на tуст / частей, чтобы было 20-30 координат: 1 30.
Задача идентификации состоит в определении (n+m) неизвестных коэффициентов b1,b2,… , bm,.a1,a2,… , anпередаточной функцииW*(p) из следующей системы уравнений
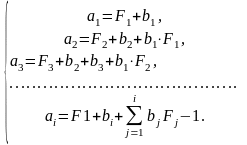 (5.7)
(5.7)
В системе уравнений i=m+n. Параметры Fi, входящие в систему уравнений, имеют (5.7) аналитические выражения
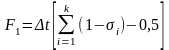 , (5.8)
, (5.8)
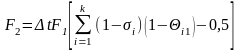 , (5.9)
, (5.9)
 . (5.10)
. (5.10)
В
формулах (5.7) – (5.10) обозначено: t
– величина интервала времени на которые
разбивается кривая разгона при ее
обработке; i
– число интервалов времени;
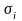 – приведенные значения выходной величины
на каждом интервале времени t;
– приведенные значения выходной величины
на каждом интервале времени t;
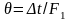 – величина интервала времени,
пересчитанного в другом масштабе.
– величина интервала времени,
пересчитанного в другом масштабе.
Идентификация объекта регулирования должна заканчиваться проверкой адекватности экспериментальной кривой разгона y(t) и считанной по найденной передаточной функции – y~(t). При проверке адекватности кривые составляют графически и количественно оценивают критерием
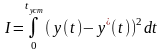 , (5.11)
, (5.11)
где tуст – время переходного процесса в объекте управления.
Пример 5.1. Записать систему уравнений для определения коэффициентов передаточной функции , для второго частного случая (5.5).
Решение:
Запишем систему алгебраических уравнений, из которых находим коэффициенты b1, a3, a2, a1:
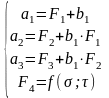 .
.
Выражения замены интеграла на сумму площадей запишутся:
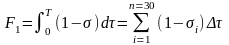 ;
;
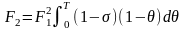 ,
,
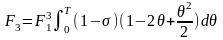 ;
;
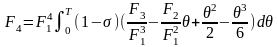 .
.
Чтобы вернуть
нормированную передаточную функцию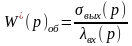 к передаточной функции объекта
к передаточной функции объекта ,
нужно первую умножить на
:
,
нужно первую умножить на
:
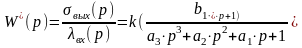 .
.
Если

 и
и
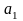 ,
то
,
то
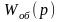 примет
вид:
примет
вид:
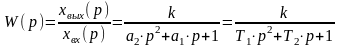 .
.
