2)Пусть :

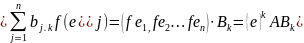
Что означает, что матрицей в базисе называется A B

№33

f лин.пр. если линейно зависимая, то лин.зависимой является каждая система (f( при этом сохраняются все линейные соотношения между векторами

Опр.Размерность пространства называется рангом линейного преобразования:

Опр.Совокупность всех векторов пространства V для которых f(V)=0 называется ядром линейного преобразования

Теорема. Ранг лин. преобр. равен рангу матрицы этого преобр. в любом базисе

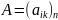матрица преобразования в данном базисе

(1), является лин. комбинацией векторов (1), но тогда каждый вектор подпространства f(v) является лин.комбинацией векторов системы ( ) (*)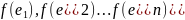

в силу равенства , rang(*)=rang(A)

Т.о. ранг преобр.f равен рангу матрицы А

№34

Теорема связь между координатами вектора и его образа Пусть f-лин.пр. в некотором фиксированном базисе пусть - произвольный вектор из V =

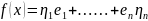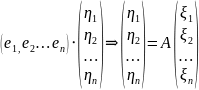
т.к.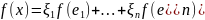 = A

№35

Теорема. Чтобы преобразование было взаимно-однозначным необходимо и достаточно, чтобы оно было невырожденным

Невырожденная матрица f Ax=0, имеет только одно решение x=0=> Kern f={0}

Из Kern f={0}=> Ax=0 имеет только одно решение => A-невырожденная

№36

Опр. Оператор В называется обратным оператору А и обозначается А ^-1, если АВ = ВА = E

Если А обратный для В, то А и В называются взаимообратными

Теорема. Чтобы f имел обратный оператор необх. и дост., чтобы он был взаимно-однознач.

Необ. (ctv) пусть f имеет обратный, но взаимн.-одноз. не является =

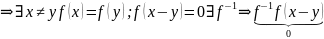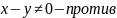
Дост. Пусть f взаимно-однозначный

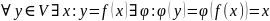легко видеть что линеен:

, ,

*

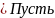
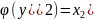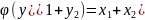
Следствия

(1)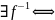 kernf=0 2)

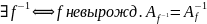
Оператор обладающий обратным—обратимый

Теорема. Каждый обратимый оператор имеет только один обратный

Ctv пусть существует дв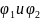а: , тогда

№37

Теорема. Пусть f имеет матрицу A в базисе и матрицу B в базисе , а

(*)

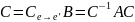
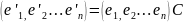т.к.

(**)

=(

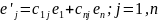
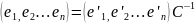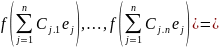
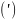
Аналогично: ( =

=

=

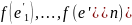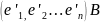
Откуда получаем B

№38

Опр. Матрица А подобна матрице В если существует такая невырожденная матрица X, что А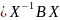

Свойства

1)Если B то В=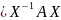 => т.о. отношение подобия симметрично

2) А

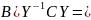
Отношение подобия транзитивно

3) каждая матрица подобна самой себе Х=Е. Отношение подобия рефлексивно. Т.о. матрицы одного и того же лин. преобр. всегда подобны

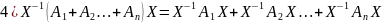
5)

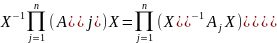
Для каждой обратимой A

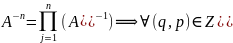
AB=BA=>

6) [ ]

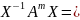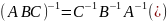7)

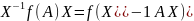
№39 Опр. . мат. ), где x— незав. переменная, называют характеристической матрицей. Её определитель f(x)=|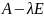 |- характеристическим многочленом оператора А.

Сумма диагональных элементов — следом(trA)

| |=0 называют характеристическим уравнением,

Теорема. Характеристические многочлены подобных матриц совпадают.

А ;

=

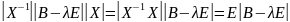
Опр. Корни | |=0 называют характеристическим числами или собственными векторами

Теорема Гамильтона-Кели: Каждая матрица является корнем своего характеристического многочлена

(В лекциях без док-в., если f-характ. многочлен, то f(А)=0)

№40

Опр. Собственным вектором оператора будем называть такой вектор, для которого выполняется равенство , 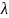называется собственным значением, соответ. собственному вектору x оператора и P(C).

Св-ва собств. вект 1) Каждому собств. вектору x соответствует (!) собственное значение .

[ctv: ]
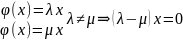