2)Пусть один из коэффициентов перед отличен от 0. Пусть для определенности . Умножая последнее из векторов на числа и вычитая из первых t векторов получим
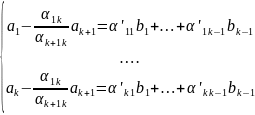
Получившееся рав-ва показывают. что k векторов, стоящие в левых частях являются лин.комб. (k-1), векторов
В силу предположения индукции система k векторов образ. левые части равенств лин.зависима, т.к. в противном случае k<k-1, что невозможно
значит,
существуют числа
из которых по крайней мере одно не равно
0, такие что
+…+
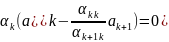
раскрыв скобки, получаем,
=>
векторы
лин.зависим, но эти векторы часть системы
(*), тогда (*) лин зависима, что противоречит
условию теоремы
№10
Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов.
Пусть
(**)
две произвольные максимально независимые
линейные системы
Докажем
что s=k.
линейно зависима => найдутся такие
числа в поле Р, не все равные 0 и такие
что
Выразим
.
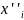Т.о. система (*) линейно выражается через
(**), аналогично система (**) линейно
выражается через (*)
В силу основной теоремы о линейной зависимости k=s
№11
Опр.
Система
векторов
линейно выражается через систему
векторов
,
если каждый вектор первой системы
линейно выражается через векторы второй
системы.
Опр. Две конечные системы векторов называются эквивалентными, если первая система векторов линейно выражается через вторую, а вторая ¾ через первую.
Теорема Ранги эквивалентных систем равны
Пусть
линейно
выражается через
,
через
,
через
,
из основной теоремы о линейной зависимости
№12
Ранг произведения не больше ранга сомножителей
№13
Опр.
Два линейных пространстваV1
и V2
называются изоморфными, если между их
элементами можно установить взаимно
однозначное соответствие, такое что:
(прос-тва над вещ. полем, пр-ва над комплексным)
Теорема. Чтобы пр-ва V и V”были изоморфны необходимо и достаточно, чтобы они имели одинаковые размерности
Возьмем
базисы
поставим в соответствие
:
V
и
изоморфны
Заметим,
что при изоморфном соотв. нулевому
вектору 0 из
из лин.зависимости
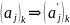и обратно
Макс. число линейно независимых векторов в обоих пространствах должно быть одинаковым
Значение Лин. прос-ва могут состоять из чего угодно (столбцов, многочл., чисел, векторов, функций) — природа элементов не влияет на свойства, связанные с лин. операциями. Все св-ва у двух изомор. пр-тв одинаковы. Если условимся не различать между собой изомор. пр-ва, то для каждой размерности найдется (!) лин. прос-во.
№14
Множество
всех решений ОСЛУ
(*) с n неизвестными над полем P, являются
лин. подпр. пр-ва Pn
тогда
b=0
Из
теоремы о линейном подпространстве
К является линейным подпространством
К называют пространством решений
Размерность К решений равна n-r, где r – ранг матрицы системы
(1)
(2)
(
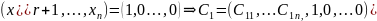
где
минор порядка
) отмечен от нуля
Докажем
что
b
(тогда
-
базис
).
Рассмотрим вспомогательный вектор
,
d(
),
где
=…=
вектор d является лин.комб. решений системы (*), а значит является её решением.
Т.о.
-решение, которое получается при нулевых
значениях неизвестных, но тогда
,
т.е. выполняется (4)
значит система векторов является базисом пр-ва К и значит пространство К является n-r мерным
№15
Опр. Вещественное линейное пространство E называется евклидовым, если в нем определена операция скалярного умножения: любым двум векторам x и у из E сопоставлено вещественное число (обозначаемое (x,y)), и это соответствие удовлетворяет следующим требованиям, для любых векторов x, у и z и числа а:
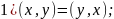
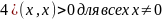
Cлед.
Неравенство Коши-Буняковского:
Если
то
верно следующее
(*)
Значит дискриминант многочлена (*) неположительный, т.е.
=>
Неравенство
(*)
Если
—аналог т.Пифагора
№16
Опр.
Базис
называется ортогональным, если векторы
(1) попарно ортогональны, если |
|=1—ортонормированным
т.е.
Теорема. Любая система попарно ортогональных векторов <>0 линейного пространства V лин.независима
)
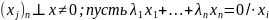
система
линейно независима
№17
Во всяком евклидовом пространстве Е" существует ортонормированный базис.
Пусть в Е" дан некоторый, неортогональный базис (g1,g2,..,gn). Построим вначале базис из попарно ортогональных элементов.
Последовательное
построение этих элементов будем называть
процессом ортогонализации базиса.
Поделив каждый из векторов на свою длину, получим ортонормированный базис
Ортогонализация Грама-Шмида
№18
Пусть
чтобы
(“)
необходимо и достаточно чтобы
–ортогональны
(*)
При ортонормированном равенство (*) переходит в (“)
Необ.
Равенство (“) подразумевает
в (*), а это и есть условие ортонормированности
Замечание
Для
произвольного x=
в ортонормированном базисе
будем
называть ()
проекцией на
Равенство () означает что координаты являются проекциями на базисные вектора
№19
Любые два евклидовых пространства одной размерности изоморфны. Евклидовы пространства разных размерностей не изоморфны.
Достаточно доказать что любое пространство изоморфно Rn
В
Евклидовом пространстве V
существует ортонормированный базис
каждому
поставлено в соответствие
пространства Rn,
установленное соответствие является
взаимно однозначным
Rn
Остается доказать что для соответствующих пар сохраняется величина скалярного произведения
Чтд
№20
Опр.Комплексное линейное пространство V называется унитарным (или эрмитовым) пространством, если задан закон, сопоставляющий каждым двум векторам x и у из V комплексное число (x,у), называемое их скалярным произведением, и этот закон удовлетворяет следующим аксиомам, каковы бы ни были векторы x, у и z и число а:
1)(
3
Следст.1.
2.
К-Б
=|(x,
y)|2
Неравенство
треугольника
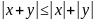
скал
произвед.
№30
Опр.
Преобразование (оператор) f
пространства V
называется линейным если:
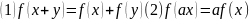
Свойства линейных преобразований
лин.преобр.
пр-ва V
то f(V)
является линейным подпространством
пространства V
то
(3) верно (по 2 елочкам)
,
а т.к. V-лин.пр.
то
z=ax+by∈V
f(z)=f(ax)+f(by)=
4)
f
лин.пр. если
линейно
зависимая, то лин.зависимой является
каждая система (f(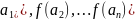
при этом сохраняются все линейные
соотношения между векторами
5)Множество
kern
является лин.подпр. пространства V
[Пусть x,
y
∈
kern;
a,
b∈P
f(ax+by)=f(ax)+f(by)=
]
6)Для взаимно-однозначного соответствия необ. И дост. Чтобы отличный от 0 вектор обращался в отличный от 0 (kern f=0 состоял из одного элемента)
7)rang+defect=dim
№31
пр-ваV
Опр.
Суммой
называется преобразование пространства,
которое для любых x
из V
задается как
Т.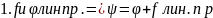
=
Сложение обладает св. ассоциативности и коммутативности
Опр.
Произведением
называется пр.пр-ва которое для любых
x
из V
задается формулой
Т.
Св. ассоциативно, но в общем случае не коммут.
Т.3умножение линейного пр. на число является лин.пр
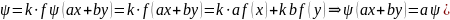
Опр.
Полиномом
называется пр.пр-ва которое для любых
x
из V
задается формулой
По т (1)-(3) полином есть линейное пр. пр-ва
№32
Опр.
Матрицей лин. преобр. в базисе
называется
мат. A:
(*)(
A.
Линейное преобразование полностью определяется вектором (*), которое определяют базис {e}n и матрицу A.
Теорема
для матриц лин.преобразований
A
и B
в базисе {e}n
матрицей преобразований является
