
Лекция6
.pdf1
ЛЕКЦИЯ № 6.
Элементы аналитической геометрии
В этом разделе будут рассмотрены множества (линии, поверхности, тела) пространств R2 и R3 с точки зрения исследования этих множеств и их свойств аналитически (с помощью формул).
Уравнением множества называется такая связь между координатами точек этого множества, которой удовлетворяют все точки, принадлежащие множеству, и не удовлетворяет ни одна из точек, не принадлежащая множеству. В декартовой системе координат пространства R3 эта связь имеет общей вид
|
F x,y,z 0. |
|
(6.1) |
Если некоторая точка |
M x1;y1;z1 принадлежит |
множеству, для |
которого |
справедливо (6.1), то |
обязательноF x1,y1,z1 0. |
Если некоторая точка |
|
N x2;y2;z2 не принадлежит этому множеству, то обязательноF x2 , y2 ,z2 |
0. |
||
Линии первого порядка
Первым объектом, который мы рассмотрим, будет прямая линия. Прямой линией является множество точек, таких что внешнее (векторное) произведение любых двух векторов, построенных на произвольно выбранных из этого множества точках, равно нулю.
Прямая линия – это объект, который задаётся уравнением вида (6.1) в пространстве R2, причём все координаты входят в это уравнение только в первой степени.
В пространстве R2 это уравнение в общем случае имеет вид
Ax By C 0, (6.2)
где А, В и С – произвольные константы.
Выразим одну из координат(у) через другую в явном виде (х):
|
|
|
|
y |
A |
x |
C |
. |
|
|
|
|
|
|
|||||
|
A |
|
C |
|
B |
B |
|
||
Обозначим k |
; b |
и получим |
|
уравнение |
прямой с угловым |
||||
B |
|
|
|||||||
|
|
B |
|
|
|
||||
коэффициентом |
|
|
y kx b . |
(6.3) |
|||||
|
|
|
|
||||||
При этом смысл постоянного параметра k – тангенс угла наклона прямой к оси Ох. Также он означает, на какую величину измениться у при увеличении х на 1: k tg .
Пусть y x kx b, тогда y x 1 k x 1 b kx k b y x k .
Если k 0, то у возрастает при увеличении х, если k 0, то – убывает.
Смысл постоянного параметра b заключается в том, что его модуль равен длине отрезка, отсекаемого прямой от оси Оу. Также он показывает, насколько далеко прямая располагается от начала координат. При b 0 прямая проходит через начало координат, поскольку подстановка в (6.3) b 0 даёт y kx. При этом точка О(0; 0) будет принадлежать прямой, т.к. подстановка нулевых координат
2
в полученное уравнение делает его истинным равенством. Если b 0, то прямая пересекает ось Оу выше начала координат, если b 0, то – ниже.
Разделим уравнение (6.3) на С:
|
|
|
|
|
A |
x |
B |
y 1 0. |
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
C |
|
C |
|
C |
C |
|
||||||
Обозначим a |
; b |
и получим уравнение прямой в отрезках |
|
||||||||||
A |
|
|
|||||||||||
|
|
B |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
y |
1, |
(6.4) |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
a b |
|
|||||
где а и b – величины отрезков, которые отсекает прямая от координатных осей. Из определения прямой линии через внешнее произведение следует то, что уравнение прямой может быть определено с помощью двух произвольных точек, принадлежащих прямой. Покажем это. Пусть две точки А(х1; у1) и В(х2; у2) принадлежат некоторой прямой. Выявим множество точек, принадлежащих этой прямой. Допустим, что произвольная точка М(х; у) тоже принадлежит прямой. Составим вектор из точек А и В: AB x2 x1; y2 y1 . Теперь составим вектор из точек А и М: AM x x1; y y1 . Эти векторы должны быть коллинеарными. Допустим, что вектор AB наклонён к оси Оу под некоторым углом α. В случае коллинеарности угол наклона вектора AM должен быть либо α, либо 180 – α. Тогда справедливо:
tg |
ABx |
|
AMx |
|
x2 |
x1 |
|
x x1 |
. |
ABy |
AMy |
y2 |
y1 |
|
|||||
|
|
|
|
y y1 |
|||||
Окончательно, перегруппировав сомножители, получим уравнение прямой, проходящей через две заданные точки
x x1 |
|
y y1 |
. |
(6.5) |
x2 x1 |
|
|||
|
y2 y1 |
|
||
Уравнение (6.5) определяет уравнение прямой, проходящей через две заданные точки.
В каждой данной точке прямой к ней можно провести одну другую прямую, перпендикулярную исходной. Эта прямая обязательно будет содержать вектор N(A;B), где А и В – константы из уравнения (6.2). Докажем это. Пусть две точки М1(х1; у1) и М2(х2; у2) принадлежат некоторой прямой. Построим из точки М1 вектор N , перпендикулярный этой прямой. Составим
вектор |
M1M2 x2 x1; y2 y1 . Если вектор N |
перпендикулярен прямой, то он |
должен |
быть перпендикулярным вектору |
M1M2 . Внутреннее (скалярное) |
произведение двух перпендикулярных векторов равно нулю. Поэтому
N,M1M2 Nx x2 x1 Ny y2 y1 0.
Поскольку прямая проходит через точку М1(х1; у1), то, согласно определению уравнения множества, уравнение (6.2) при подстановке координат этой точки должно превращаться в истинное равенство. Тогда Ax1 By1 C 0. Вычтем это уравнение из (6.2), чтобы избавиться от свободного коэффициента С
Ax By C Ax1 By1 C 0 A x x1 B y y1 0.

3
Получим аналогично уравнение прямой, проходящей через точку М2(х2; у2):
Ax By C Ax2 By2 C 0 A x x2 B y y2 0.
Вычтем из первого уравнения второе
A x x1 B y y1 A x x2 B y y2 0 A x2 x1 B y2 y1 0.
Теперь сравним полученный результат с результатом внутреннего (скалярного) произведения
N |
|
x |
|
x N |
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
|
|
2 |
|
|
1 |
|
y |
|
2 |
1 |
Nx A; Ny B N A;B . |
|
|
|
|
|
|
|
|||||||
|
A x |
2 |
x B y |
2 |
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Две прямые перпендикулярны друг другу, если при задании их |
||||||||||||||||||||||||||||
уравнениями с угловым коэффициентом |
(6.3) y k1x b1 и |
y k2 x b2 |
угловые |
|||||||||||||||||||||||||
коэффициенты |
k |
1 |
|
1 |
. |
|
|
|
Покажем |
это. |
Пусть заданы |
две |
прямые, |
|||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
перпендикулярные |
|
друг |
другу, общими |
уравнениями |
A1x B1 y C1 |
0 |
и |
|||||||||||||||||||||
A2 x B2 y C2 0. |
Тогда |
вектор |
|
N1(A1;B1) |
перпендикулярен |
первой прямой, |
а |
|||||||||||||||||||||
вектор N2 (A2;B2 ) |
|
– второй прямой. Если прямые перпендикулярны, то и |
||||||||||||||||||||||||||
векторы N1 и N2 |
|
также будут перпендикулярны. Внутреннее (скалярное) |
||||||||||||||||||||||||||
произведение двух перпендикулярных векторов равно нулю, поэтому |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N1,N2 A1A2 B1B2 0. |
|
A1 |
|
|
|
|
A2 |
|
||||||||||
Согласно обозначениям, |
введённым |
при выводе (6.3) k |
|
, а |
k |
2 |
|
. |
||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
B1 |
|
|
|
B2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разделим полученное уравнение на B1B2 :
A1 A2 1 0 k1k2 1.
B1B2
Это соотношение определяет указанное выше соотношение между угловыми коэффициентами перпендикулярных прямых.
Две прямые параллельны друг другу, если при задании их уравнениями с
угловым коэффициентом (6.3) |
y k1x b1 и y k2 x b2 угловые коэффициенты |
||||||||
k1 k2 , |
|
либо при задании |
общим уравнением (6.1) A1x B1 y C1 0 и |
||||||
A x B |
2 |
y C |
2 |
0 коэффициенты при неизвестных пропорциональны |
A1 |
|
B1 |
. |
|
|
|
||||||||
2 |
|
|
|
A2 |
|
B2 |
|||
|
|
|
|
|
|
|
|||
Если точка не принадлежит прямой, то говорят, что прямая проходит на некотором ненулевом кратчайшем расстоянии от этой точки. Определим это расстояние. Пусть имеется произвольная точка Р(хР; уР) с известными координатами и уравнение прямой L Ax By C 0. Построим прямую, параллельную L и проходящую через точку Р. Выберем произвольно точку М(х; у) на прямой L, но не лежащую на перпендикуляре из точки Р на прямую L. Построим вектор PM x xP ; y yP . Построим из точки М вектор, перпендикулярный прямой L N(A;B). Тогда расстояние от точки Р до прямой L будет равно модулю проекции вектора PM на вектор N .
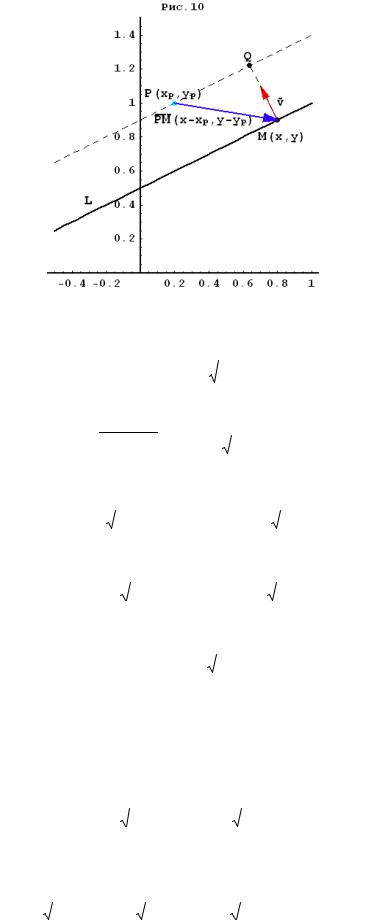
4
Из приложения внутреннего (скалярного) произведения
|
прx1x2 |
|
|
x1 |
, x2 |
|
|
11 12 21 |
|
22 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Подставляем: |
|
|
|
|
PM, N |
|
|
|
|
|
|
|
11 |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x xP |
|
A y yP B |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||
прN PM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Преобразуем, раскрыв скобки |
A y y |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
x x |
P |
P |
|
|
|
Ax Ax |
P |
By By |
P |
. |
|||||||||||||||||||||||||||||||||||
прN PM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
B2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Из (6.2) Ax By C . Подставляем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Ax Ax |
P |
By By |
P |
|
|
|
|
|
Ax |
P |
|
By |
P |
C |
. |
|
|
||||||||||||||||||||||||||||
прN PM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|||||||||||||||||||||||||
Тогда искомое расстояние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax |
|
|
|
|
By |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
P |
|
|
|
|
|
|
|
|
|
(6.6) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
h |
прN PM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
есть кратчайшее расстояние между точкой Р и прямой L.
Основываясь на полученных результатах, запишем ещё одно уравнение прямой через перпендикуляр, опущенный на прямую из начала координат. Используем формулу (6.6) для определения расстояния от начала координат до прямой, учитывая, что О(0; 0).
|
|
p |
A 0 |
|
B 0 |
C |
|
|
|
|
C |
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
A2 B2 |
|
|
|
|
|
A2 B2 |
|
|
|||
Разделим далее общее уравнение прямой на |
норму вектора N(A;B), |
|||||||||||||||||
перпендикулярного этой прямой |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
A |
|
x |
|
|
B |
|
y |
|
|
|
C |
|
0. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
A2 B2 |
|
|
A2 B2 |
|
A2 B2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
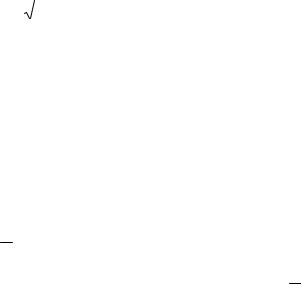
5
A
Тогда выражение  представляет собой косинус угла наклона
представляет собой косинус угла наклона

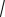 A2 B2
A2 B2
перпендикуляра к оси |
Ох, а |
|
|
B |
|
– синус этого угла. |
Преобразуем |
|
|
|
|
|
|||||
A2 |
B2 |
|||||||
полученное выражение: |
|
|
|
|
|
|||
xCos ySin p 0. |
(6.7) |
|||||||
|
||||||||
Уравнение (6.7) представляет собой нормальное уравнение прямой.
Получим уравнение прямой, проходящей через заданную точку и перпендикулярной другой прямой. Пусть известно, что прямая проходит через точку М1(х1; у1). Тогда уравнение прямой, проходящей через эту точку, будет иметь вид
A x x1 B y y1 0.
Разделим это уравнение на коэффициент В
A x x1 y y1 0. B
Ранее было введено обозначение углового коэффициента как k A, поэтому
|
|
|
|
k x x1 y y1 0. |
|
B |
|
||
|
|
|
|
|
|
|
|||
Теперь |
используем |
условие |
перпендикулярности. |
Пусть |
прямая, |
||||
перпендикулярная исходной прямой, задана уравнением |
y k1x b1. |
В силу |
|||||||
перпендикулярности k |
1 |
. Подставляем в уравнение |
|
|
|||||
|
|
|
|||||||
|
|
|
k1 |
1 |
|
|
|
|
|
|
|
|
|
|
x x y y 0. |
|
(6.8) |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
k1 |
|
|
|
|
Уравнение (6.8) – искомое уравнение прямой, проходящей через заданную точку и перпендикулярной другой прямой.
Пусть заданы две |
произвольные прямые уравнениями с угловым |
||
коэффициентом |
(6.3) y k1x b1 |
и y k2 x b2 . Определим угол, который они |
|
образуют между |
собой. |
Пусть |
одна прямая образует с положительным |
направлением оси Ох угол α1, а другая – α2. Причём tg 1 k1 , а tg 2 k2 . Очевидно, что угол между прямыми будет α2 – α1. Для определения его тангенса используем тригонометрическую формулу для тангенса разности
tg 2 |
1 |
|
tg 2 tg 1 |
|
k2 k1 |
. |
(6.9) |
|
|
||||||
|
|
1 tg 1 tg 2 |
1 k1k2 |
|
|||
Проверим правильность этого результата. Если прямые параллельны, то k1 k2 . Подстановка этого равенства в (6.9) обращает числитель правой части (6.9) в ноль. Если тангенс угла равен нулю, то и сам угол равен нулю, следовательно, прямые параллельны. Если прямые перпендикулярны, то k1k2 1. Эта подстановка обращает в ноль знаменатель правой части (6.9). Тогда тангенс бесконечен, а угол между прямыми равен 900.
Рассмотрим пространство R3. Вернёмся к уравнению (6.1) и построим объект, аналогичный уравнению (6.2) такой, что все координаты будут входить в уравнение этого множества в первой степени

6
Ax By Cz D 0, |
(6.10) |
где А, В, С и D – произвольные константы.
Однако это уже не прямая. К данной точке прямой в пространстве R2 можно построить только одну другую прямую, перпендикулярную исходной. Эта прямая будет содержать вектор с координатами N(A;B), где А и В – константы из уравнения (6.2). В пространстве R3 к данной точке прямой можно построить бесконечное множество прямых, перпендикулярных исходной. К объекту, описываемому уравнением (6.10), можно построить только одну перпендикулярную прямую из заданной точки объекта. Эта прямая будет содержать вектор N(A;B;C).
Объект (множество точек), описываемый уравнением (6.10) является
плоскостью.
Плоскостью является такое множество точек, для которого смешанное произведение векторов, составленных из трёх произвольных его точек, всегда равно нулю.
Рассмотрим способы задания плоскости.
Пусть известен вектор N(A;B;C), перпендикулярный плоскости, и точка М(х1; у1; z1), принадлежащая плоскости. Координаты вектора N определяют коэффициенты уравнения (6.10). Тогда неизвестным остаётся только коэффициент D. Если точка М принадлежит плоскости, то, согласно определению уравнения множества, подстановка её координат в (6.10) должно давать истинное равенство, т.е.
Ax1 By1 Cz1 D 0.
Отнимем полученное уравнение из уравнения (6.6):
Ax By Cz D Ax1 By1 Cz1 D 0.
Или окончательно
A x x1 B y y1 C z z1 0. |
(6.11) |
Уравнение (6.11) определяет плоскость, проходящую через заданную точку перпендикулярно заданному вектору.
Пусть известны длины трёх отрезков, отсекаемых плоскостью от координатных осей. Разделим уравнение (6.10) на коэффициент D
A x B y C z 1 0. D D D
Обозначим a |
D |
; b |
D |
; c |
D |
и получим уравнение плоскости в отрезках |
|||||||
A |
B |
|
|||||||||||
|
|
|
C |
|
|||||||||
|
|
|
|
|
|
|
x |
|
y |
|
z |
1, |
(6.12) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
a b c |
|
|||||
где a, b и c – величины отрезков, которые плоскость отсекает от координатных осей.
Поскольку смешанное произведение трёх компланарных (лежащих в одной плоскости) векторов равно нулю, то плоскость однозначно определяется тремя точками, не лежащими на одной прямой. Действительно, рассмотрим произвольный векторный треугольник, построенный на векторах как на сторонах. Треугольник представляет собой двумерный объект, задать который

7
можно однозначно с помощью трёх его вершин. Через него можно провести единственную плоскость. Таким образом, через три точки, не лежащие на одной прямой, можно провести единственную плоскость.
Рассмотрим уравнение плоскости, проходящей через три заданные точки М1(х1; у1; z1), М2(х2; у2; z2) и М3(х3; у3; z3), не лежащие на одной прямой. Поскольку плоскость проходит через точку М1(х1; у1; z1), то, согласно (6.11) получаем
A x x1 B y y1 C z z1 0.
Аналогично
A x x2 B y y2 C z z2 0. A x x3 B y y3 C z z3 0.
Вычтем из первого уравнения второе и третье
A x2 x1 B y2 y1 C z2 z1 0. A x3 x1 B y3 y1 C z3 z1 0.
Составим систему уравнений
A x x1 B y y1 C z z1 0A x2 x1 B y2 y1 C z2 z1 0.
A x3 x1 B y3 y1 C z3 z1 0
Эта система уравнений имеет либо тривиальное решение A B C 0, либо её определитель равен нулю. Однако при тривиальном решении вектор, перпендикулярный плоскости N(A;B;C) будет также тривиальным. Поэтому искомым уравнением плоскости будет равенство нулю определителя системы
x x1 |
y y1 |
z z1 |
0. |
(6.13) |
x2 x1 |
y2 y1 |
z2 z1 |
||
x3 x1 |
y3 y1 z3 z1 |
|
|
|
Уравнение (6.13) представляет собой уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой.
Вернёмся к заданию плоскости с помощью векторов. Пусть заданы два произвольных вектора, имеющих общее начало. Третий вектор, принадлежащий этой плоскости, не может быть построен произвольно, поскольку должен удовлетворять условию компланарности. Таким образом, два независимых, имеющих общее начало вектора, образуют единственную плоскость. Это легко показать. Допустим, что два вектора, имеющих общее начало, образуют две плоскости. Построим третий вектор, который соединяет концы исходных векторов. Он удовлетворяет условиям компланарности с двумя исходными векторами. Поэтому должен принадлежать обеим плоскостям, которые образуют эти исходные векторы. Однако построенные три вектора образуют единственный треугольник (двумерный объект), который может принадлежать только одной плоскости. Получили противоречие, которое говорит о том, что мы сделали неверное допущение. Следовательно, через два исходных вектора, имеющих общее начало, можно провести только одну плоскость. Эти векторы определяют две прямые, пересекающиеся в их общем
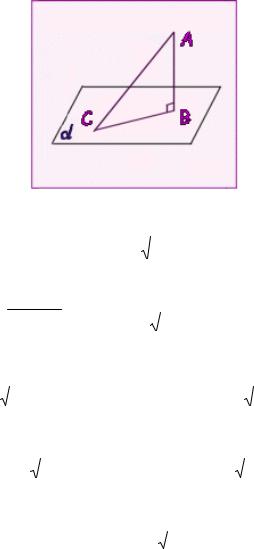
8
начале. Поэтому плоскость может быть задана двумя пересекающимися прямыми.
Если точка не принадлежит плоскости, то говорят, что плоскость проходит на некотором ненулевом кратчайшем расстоянии от этой точки. Определим это расстояние. Пусть имеется произвольная точка Р(хР; уР; zР) с известными координатами и уравнение плоскости L Ax By Cz D 0. Построим произвольную прямую, проходящую через точку Р и пересекающую плоскость в некоторой точке Q. Эта прямая называется наклонной к плоскости. Построим вектор, перпендикулярный прямой L N(A;B;С) и проходящий через точку Р. Начало этого вектора будет располагаться в точке S, которая называется основанием перпендикуляра. Построим вектор PQ x xP ; y yP ; z zP . Тогда расстояние от точки Р до плоскости L будет равно модулю проекции вектора PM на вектор N .
Из приложения внутреннего (скалярного) произведения
|
|
|
|
прx1x2 |
|
x1 |
, |
x2 |
|
11 12 |
21 |
22 |
|
31 32 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Подставляем: |
|
|
|
|
PQ, N |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
21 |
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x xP A y yP B z zP C |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
прN PQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Преобразуем, раскрыв скобки |
|
B z z |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x x |
P |
A |
y y |
P |
P |
|
|
|
|
|
Ax Ax |
P |
By By |
P |
Cz Cz |
P |
. |
||||||||||||||||||||||||||||||||||||||
прN PQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Из (6.10) Ax By Cz D. Подставляем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
Ax Ax |
P |
By By |
P |
Cz Cz |
P |
|
|
|
|
Ax |
P |
|
By |
P |
Cz |
P |
D |
. |
|
|
||||||||||||||||||||||||||||||||
прN PQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
|
|
||||||||||||||||||||||||||||||||
Тогда искомое расстояние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax |
|
|
By |
|
Cz |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
P |
P |
|
|
|
|
|
|
|
|
|
(6.14) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
h |
прN PQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
есть кратчайшее расстояние между точкой Р и плоскостью L.
Получим нормальное уравнение плоскости, основой которого является перпендикуляр, опущенный на плоскость из начала координат. Используем формулу (6.14) для определения расстояния от начала координат до плоскости, учитывая, что О(0; 0; 0).

9
|
|
|
|
|
p |
|
A 0 |
B 0 C 0 D |
|
|
|
|
|
|
D |
|
|
|
. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|||||||||||||||||
Разделим далее общее уравнение плоскости на норму вектора |
N(A;B;C), |
|||||||||||||||||||||||||||||||||||||||
перпендикулярного этой плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
A |
|
|
|
x |
|
|
|
|
|
B |
y |
|
|
|
C |
|
|
|
z |
|
|
|
D |
|
|
0. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
A2 B2 C2 |
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
A2 B2 C2 |
|
||||||||||||||||||||
Тогда выражение |
|
|
|
|
|
|
|
A |
|
|
|
представляет собой |
косинус |
угла |
наклона |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
A2 B2 C2 |
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
перпендикуляра |
к |
|
|
оси |
|
Ох, |
|
|
|
|
|
– |
|
|
косинус |
угла |
наклона |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
A2 B2 C2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
перпендикуляра |
к |
|
оси |
Оу, а |
|
|
|
|
|
|
C |
|
|
– |
косинус |
угла |
наклона |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
A2 |
B2 C2 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
перпендикуляра к оси Оz. Преобразуем полученное выражение: |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xCos yCos zCos p 0. |
|
|
|
|
|
|
|
(6.15) |
||||||||||||||||||||
Уравнение (6.15) представляет собой нормальное уравнение плоскости. |
||||||||||||||||||||||||||||||||||||||||
Две плоскости являются параллельными, если |
векторы |
N1(A1;B1;C1) и |
||||||||||||||||||||||||||||||||||||||
N2 (A2;B2;C2 ), перпендикулярные этим плоскостям, коллинеарные векторы, т.е. |
||||||||||||||||||||||||||||||||||||||||
их внешнее (векторное) произведение равно нулю |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N1,N2 0. |
|
|
|
|
|
|
|
|
|
|
|
(6.16) |
||||||||||
Уравнение (6.16) означает, что координаты этих векторов, которые являются константами в общем уравнении плоскости (6.10), должны быть пропорциональными
A1 B1 C1 .
A2 B2 C2
Параллельные плоскости в Евклидовом пространстве R3 не имеют общих элементов, т.е. не пересекаются.
Две плоскости являются перпендикулярными, если векторы N1(A1;B1;C1) и N2 (A2;B2;C2 ), перпендикулярные этим плоскостям, также перпендикулярны друг другу, т.е. их внутреннее (скалярное) произведение равно нулю
N1,N2 0. |
(6.17) |
Уравнение (6.17) даёт связь между координатами этих векторов: |
|
A1A2 B1B2 C1C2 0. |
|
Перпендикулярные плоскости в Евклидовом пространстве R3 |
имеют общий |
элемент, который является прямой линией, т.е. плоскости пересекаются по прямой линии. Угол между плоскостями составляет 900.
Если плоскости не являются параллельными или перпендикулярными, то в пространстве R3 они пересекаются по прямой. Угол, который они образуют между собой, соответствует углу между векторами N1(A1;B1;C1) и N2 (A2;B2;C2 ), перпендикулярными этим плоскостям. Его можно определить, используя внутреннее (скалярное) произведение этих векторов
Cos |
N1 |
,N2 |
|
|
A1A2 |
B1B2 C1C2 |
|
|
. |
(6.18) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
N |
1 |
|
N |
2 |
|
|
|
A2 |
B2 |
C2 |
|
A2 |
B2 |
C2 |
|
||
|
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
|||

10
Прямая в пространстве R3
Ранее было отмечено, что пересечением двух непараллельных плоскостей
впространстве R3 является прямая линия. Поэтому общим уравнением прямой
впространстве R3 можно считать общую часть двух плоскостей:
A1x B1 y C1z D1 0,A2 x B2 y C2 z D2 0.
При этом плоскости не должны быть параллельными, т.е., согласно (6.16) не выполняются условия
A1 B1 C1 .
A2 B2 C2
В пространстве R3 будем определять направление прямой с помощью направляющего вектора, который параллелен этой прямой. Пусть задана некоторая прямая и направляющий вектор S m,n, p , который не принадлежит этой прямой, и некоторая точка М(х1; у1; z1). Выберем произвольную точку Р(х; у; z), принадлежащую прямой. Построим вектор MP x x1; y y1; z z1 . Очевидно, что он будет перпендикулярен направляющему вектору S . Поэтому должно выполняться условие параллельности этих векторов
x x1 |
|
y y1 |
|
z z1 |
. |
(6.19) |
m |
n |
|
||||
|
|
p |
|
|||
Уравнение (6.19) называется каноническим уравнением прямой. Каноническое уравнение можно привести к параметрическому виду. Обозначим
|
x x1 |
|
|
y y1 |
|
z z1 |
t . |
|
||||||
|
|
|
|
|
|
|
||||||||
|
m |
|
|
|
|
n |
|
|
|
p |
|
|
||
Тогда получим систему уравнений |
|
|
|
|
|
|
|
|
|
|
||||
|
x x |
|
t |
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
x x |
mt |
|
|||||||
|
|
|
|
|
|
|
||||||||
|
y y |
|
|
|
|
1 |
nt . |
(6.20) |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
t |
y y1 |
||||||
|
|
n |
|
|
||||||||||
|
|
|
|
|
|
z z |
pt |
|
||||||
|
z z |
1 |
|
t |
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
p |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнения (6.20) представляют собой параметрические уравнения прямой. Такими уравнениями в механике задаются уравнения прямолинейного равномерного движения материальной точки в пространстве R3.
Пусть две точки М1(х1; у1; z1) и М2(х2; у2) принадлежат прямой. Выберем произвольным образом третью точку М(х; у; z), также принадлежащую этой
прямой. |
Составим |
два |
вектора |
|
M1М x x1; y y1; |
z z1 |
и |
||||
M2М x2 |
x1; y2 y1; z2 z1 . |
Они должны быть коллинеарными, |
поскольку |
||||||||
принадлежат одной прямой. Поэтому справедливо |
|
|
|||||||||
|
|
|
x x1 |
|
|
y y1 |
|
z z1 |
. |
|
(6.21) |
|
|
|
|
|
y2 y1 |
|
|
||||
|
|
|
x2 x1 |
|
z2 z1 |
|
|
||||
