61. Понятие о форме и размерах земли. Референц-эллипсоид Красовского. Системы координат, применяемая в геодезии.

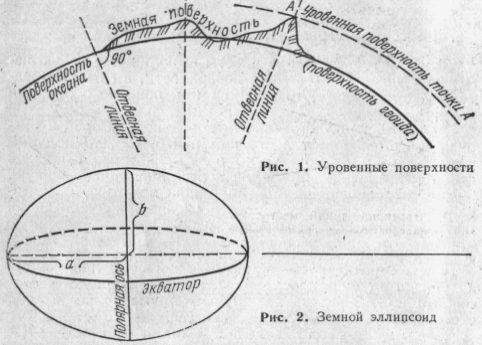
Если мысленно продолжить поверхность морей и оке­анов в их спокойном состоянии под сушей, то получим уровенную поверхность, которая в каждой своей точке перпендикулярна к отвесной линии. Фигура Земли, ограниченная уровенной поверхностью, совпада­ющей с поверхностью Мирового океана и продолженная под материками, называется геоидом. Уровенную поверхность, параллельную поверхности геоида, можно мысленно провести через любую точку, например точку А (рис. 1).

Средний уровень Балтийского моря, отмеченный чер­той Кронштадтского футштока, в принят за исход­ную уровенную повер-ть, от которой отсчитывают вы­соты точек зем повер-ти.

Поверхность геоида из-за влияния центробежной силы и неравномерного распределения масс внутри Земли гео­метрически неправильна и не может быть выражена ма­тематической формулой. Поэтому за форму Земли при­нимают эллипсоид вращения (рис. 2), кото­рый имеет наименьшие отклонения от поверхности геоида. Референц- элепсоид – элепсоид с определен размерами и ориентировкой, на поверхность к. переносят результаты геодез и картограф работ.

Поверхность эллипсоида получается от 'вращения эл­липса вокруг его полярной оси. Отношение разности полу­осей а и Ь к большой полуоси а, эллипсоида называется сжатием и выражается формулой а =(а — Ь)/а.

В нашей стране с 1946 г. для всех геодезических работ принят референц-эллипсоид Красовского с параметрами а = 6 378 245 м, Ъ = 6 356 863 м, а = 1 : 298,3.

Для решения многих практических вопросов сжатие земного эллипсоида не учитывают и фигуру Земли при­нимают за шар радиусом 6370 км.

Положение т-ки на зем поверх или на плоскости опред. известными величинами (координатами). В геодез использ. несколько сист координат: географич, прямоуг, полярные и биполярные.

В географ. сист. положение т-ки, лежащ на зем поверхн, опред географ. широтой и долготой. Мередиан – след сечения поверх-сти плоскостью проходящей через ось мира. Угол ф наз географ широтой – острый угол, образованный нормалью к поверхности элепсоида в данной точке и плоскостью экватора. Угол λ наз географ долготой – двухгранный угол, образованный плоскостью гринвического мередиана и плоскостью мередиана, проходящего через данную точку. Прямая хх— наз осевой меридиан, а уу — перпендикулярная к оси абсцисс, называется осью ординат или осью игреков. Точка пересечения осей принимается за начало координат. y — абсцисса, х — ордината.

Прямоугольн си-ма корд: декардовая си-ма – частная си-ма корд. Корд-ми осями в этой си-ме явл ось ОХ – линия с положительным направлением на север, ось ОУ – с положит напрвлением на восток. Начало корд произвольно. Использ-ют декартовую си-му для съемки небольшого уч-ка. Прямоугольн си-ма коорд Гаусса: в каждой зоне вводят си-му плоских прямоугольн корд, за ось обцис принемают осевой мередиан зон, за ось ординат – экватор, чтобы не иметь отриц-ые корд, за начало счета принимают 500км в 6⁰ зонах и 250 в 3⁰ зонах. Если в зоне провести провести линии параллельны осев-му меред-ну и экватору, то получим корд сетку.

Полярная си-ма – использ-ся при съемке деталей местности (полярная ось – произвольно.), полярный угол α идет только по часовой стрелке (360⁰). Сущность полярной си-мы корд заклю­ч-ся в следующем. На горизонтальной плоскости через выбранную точку О (рис. 9), называемую полюсом, проведем линию Ох, называемую полярной осью. Отложим по ходу часовой стрелки от оси Ох угол р\ и проведем прямую через полюс О. Отложив на этой пря­мой расстояние г_1л получим положение искомой точки А. Расстояние О А называется радиусом-вектором точки А.

В биполярной системе координат на плоско­сти выбирают два полюса О_х и О₂ (рис. 10), которые со­единяют прямой, называемой полярной осью. Для по­лучения положения точки А откладывают от полярной

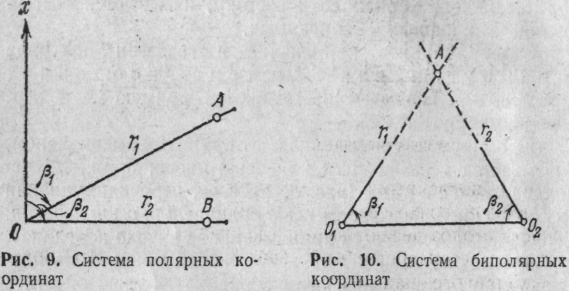
оси углы р\ и Р₂ и проводят через полюсы радиусы-век­торы г_г и г₂. На их пересечении получим искомую то­чку А.