Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
Кафедра МО ЭВМ
Вычислительная математика
Отчет
по выполнению лабораторной работы N6
Преподаватель: Щеголева Н.Л.
Студент группы 4351: Усенко А.В.
Санкт-Петербург, 2006
Постановка задачи
Необходимо исследовать обусловленность
задачи нахождения корня уравнения
для нелинейной функции
(Вариант 16). Значение корня х
вычисляется с помощью метода простых
итераций. Функция вычисляется приближенно,
с точностью Delta, варьируемой в пределах
от 0.1 до 0.000001. Корень уравнения вычисляется
с заданной точностью Eps, варьируемой от
0.1 до 0.000001. Вычисления провести для
различных наборов параметров Delta, Eps.
-
Графически или аналитически отделить корень уравнения
. -
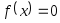Преобразовать уравнение
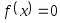к виду
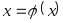так, чтобы в некоторой окрестности
[Left,
Right]
корня производная
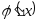удовлетворяла условию 
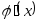q.
При этом следует иметь в виду, что чем
меньше величина q,
тем быстрее последовательные приближения
сходятся к корню. -
Выбрать начальное приближение, лежащее на [Left, Right].
-
Составить подпрограмму для вычисления значений
,
,
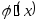предусмотрев округление вычисленных
значений с точностью Delta. -
Составить головную программу, вычисляющую корень уравнения и содержащую обращение к программам
,
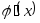и ITER
и индикацию результатов. -
Провести вычисления по программе. Исследовать скорость сходимости и обусловленность метода.
Общие сведения
Метод
простых итераций решения уравнения
состоит в замене исходного уравнения
эквивалентным ему уравнением x=(x)
и построении последовательности
xn+1=(xn),
сходящейся при n
к точному решению. Достаточные условия
сходимости метода простых итераций
формулируются теоремой, приведенной
[1,2,7].
Рассмотрим
один шаг итерационного процесса. Исходя
из найденного на предыдущем шаге значения
xn-1,
вычисляется y=
(xn-1).
Если
,
то полагается xn=y
и выполняется очередная итерация. Если
же
,
то вычисления заканчиваются и за
приближенное значение корня принимается
величина xn=y.
Погрешность результата вычислений
зависит от знака производной
:
при
>0
погрешность определения корня составляет
qq,
а при
<0
погрешность не превышает .
Здесь q-
число, такое, что 
q
на отрезке [a,b].
Существование числа q
является условием сходимости метода в
соответствии с отмеченной выше теоремой.
Для
применения метода простых итераций
определяющее значение имеет выбор
функции
в уравнении
,
эквивалентном исходному. Функцию
необходимо подбирать так, чтобы 
q.
Это обусловливается тем, что если
<0
на отрезке [a,b],
то последовательные приближения
xn=(xn-1)
будут колебаться около корня c,
если же
>0,
то последовательные приближения будут
сходиться к корню c
монотонно. Следует также помнить, что
скорость сходимости последовательности
{xn}
к корню c
функции
тем выше, чем выше число q.
Анализ задачи
По графику функции можно произвести отделение корня.
График функции:
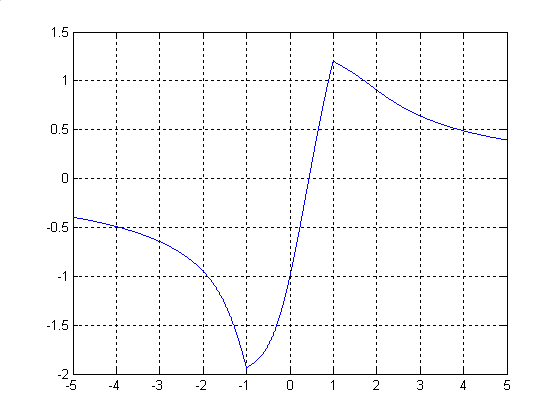
Теоретическое абсолютное число
обусловленности
.
Погрешность вычисления корня определяется
по формуле:
.
Если практическая погрешность вычисления
корня больше или равна теоретический,
то задача хорошо обусловлена, иначе –
плохо обусловлена.
Функция:
Производная:
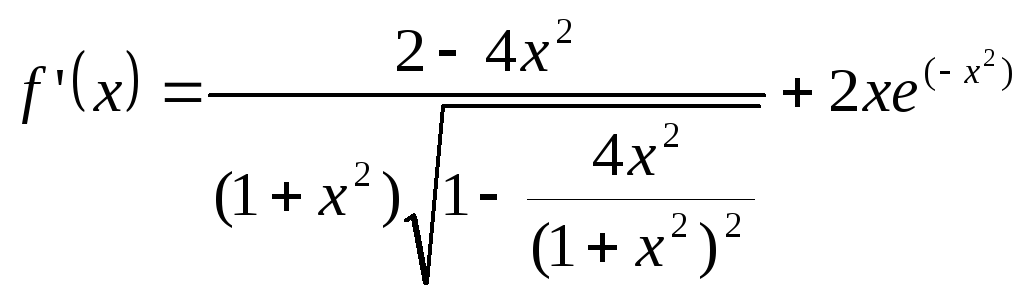
Итерационная функция:
,
где M=max(f ’(x)), x [Left; Right]
m=min(f ’(x)), x [Left; Right]
Для отделения корня, выбора границ [Left; Right] и выбора начального приближения рассмотрим следующую таблицу значений функций и их производных на интервале [0;1]:
Таблица значений:
|
X F(x) F'(x) Fi(x) Fi'(x)
0.00 -1.000000000 2.000000000 0.444444400 0.111111100 0.01 -0.979900700 2.019798000 0.445511400 0.102312000 0.02 -0.959605400 2.039184300 0.446491300 0.093695900 0.03 -0.939118400 2.058147600 0.447386000 0.085267700 0.04 -0.918443900 2.076677200 0.448197300 0.077032400 0.05 -0.897586300 2.094762800 0.448927200 0.068994300 0.06 -0.876550200 2.112394600 0.449577900 0.061158000 0.07 -0.855340000 2.129563500 0.450151100 0.053527300 0.08 -0.833960500 2.146260700 0.450649100 0.046106400 0.09 -0.812416400 2.162478100 0.451074000 0.038898600 0.10 -0.790712500 2.178208000 0.451427800 0.031907600 0.11 -0.768853900 2.193443400 0.451712800 0.025136300 0.12 -0.746845300 2.208177600 0.451931200 0.018587700 0.13 -0.724692000 2.222404600 0.452085300 0.012264600 0.14 -0.702398900 2.236119000 0.452177300 0.006169300 0.15 -0.679971300 2.249315600 0.452209500 0.000304200 0.16 -0.657414400 2.261990000 0.452184200 -0.005328900 0.17 -0.634733300 2.274138100 0.452103700 -0.010728000 0.18 -0.611933400 2.285756600 0.451970400 -0.015891800 0.19 -0.589019900 2.296842300 0.451786600 -0.020818800 0.20 -0.565998300 2.307392700 0.451554800 -0.025507900 0.21 -0.542873900 2.317405800 0.451277300 -0.029958100 0.22 -0.519652000 2.326880000 0.450956400 -0.034168900 0.23 -0.496338100 2.335814100 0.450594700 -0.038139600 0.24 -0.472937500 2.344207300 0.450194400 -0.041869900 0.25 -0.449455700 2.352059500 0.449758100 -0.045359800 0.26 -0.425898100 2.359370600 0.449288000 -0.048609200 0.27 -0.402270100 2.366141300 0.448786700 -0.051618400 0.28 -0.378577100 2.372372300 0.448256500 -0.054387700 0.29 -0.354824500 2.378065100 0.447699800 -0.056917800 0.30 -0.331017600 2.383221100 0.447118900 -0.059209400 0.31 -0.307161800 2.387842400 0.446516400 -0.061263300 0.32 -0.283262500 2.391931300 0.445894400 -0.063080600 0.33 -0.259325000 2.395490400 0.445255600 -0.064662400 0.34 -0.235354500 2.398522700 0.444602000 -0.066010100 0.35 -0.211356300 2.401031300 0.443936100 -0.067125000 0.36 -0.187335600 2.403019900 0.443260300 -0.068008800 0.37 -0.163297600 2.404492200 0.442576700 -0.068663200 0.38 -0.139247400 2.405452200 0.441887700 -0.069089900 0.39 -0.115190200 2.405904300 0.441195600 -0.069290800 0.40 -0.091131000 2.405853000 0.440502700 -0.069268000 0.41 -0.067074800 2.405303000 0.439811000 -0.069023600 0.42 -0.043026600 2.404259400 0.439122900 -0.068559700 0.43 -0.018991300 2.402727300 0.438440600 -0.067878800 0.44 0.005026300 2.400712200 0.437766100 -0.066983200 0.45 0.029021400 2.398219500 0.437101600 -0.065875300 0.46 0.052989100 2.395255100 0.436449300 -0.064557800 0.47 0.076924900 2.391824800 0.435811200 -0.063033200 0.48 0.100824100 2.387934900 0.435189300 -0.061304400 0.49 0.124682100 2.383591400 0.434585700 -0.059374000 0.50 0.148494400 2.378800800 0.434002500 -0.057244800 0.51 0.172256700 2.373569600 0.433441500 -0.054919800 0.52 0.195964400 2.367904500 0.432904700 -0.052402000 0.53 0.219613300 2.361812200 0.432394100 -0.049694300 0.54 0.243199200 2.355299700 0.431911500 -0.046799900 0.55 0.266717900 2.348374000 0.431458700 -0.043721800 0.56 0.290165300 2.341042100 0.431037600 -0.040463200 0.57 0.313537400 2.333311400 0.430650000 -0.037027300 0.58 0.336830300 2.325189200 0.430297600 -0.033417400 0.59 0.360040000 2.316682800 0.429982200 -0.029636800 0.60 0.383162700 2.307799800 0.429705500 -0.025688800 0.61 0.406194700 2.298547800 0.429469000 -0.021576800 0.62 0.429132400 2.288934400 0.429274500 -0.017304200 0.63 0.451972200 2.278967300 0.429123500 -0.012874400 0.64 0.474710600 2.268654400 0.429017500 -0.008290800 0.65 0.497344200 2.258003500 0.428958100 -0.003557100 0.66 0.519869600 2.247022600 0.428946800 0.001323300 0.67 0.542283600 2.235719600 0.428985100 0.006346800 0.68 0.564582900 2.224102600 0.429074300 0.011510000 0.69 0.586764600 2.212179600 0.429215700 0.016809100 0.70 0.608825500 2.199958800 0.429410900 0.022240500 0.71 0.630762800 2.187448400 0.429661000 0.027800700 0.72 0.652573600 2.174656400 0.429967300 0.033486000 0.73 0.674255000 2.161591300 0.430331100 0.039292800 0.74 0.695804500 2.148261100 0.430753600 0.045217300 0.75 0.717219400 2.134674200 0.431235800 0.051255900 0.76 0.738497200 2.120839000 0.431779000 0.057404900 0.77 0.759635400 2.106763600 0.432384300 0.063660600 0.78 0.780631700 2.092456400 0.433052600 0.070019400 0.79 0.801483800 2.077925800 0.433785000 0.076477400 0.80 0.822189500 2.063180100 0.434582400 0.083031100 0.81 0.842746700 2.048227500 0.435445900 0.089676700 0.82 0.863153300 2.033076500 0.436376300 0.096410400 0.83 0.883407600 2.017735400 0.437374400 0.103228700 0.84 0.903507500 2.002212400 0.438441100 0.110127800 0.85 0.923451200 1.986515800 0.439577200 0.117104100 0.86 0.943237200 1.970653800 0.440783500 0.124153900 0.87 0.962863800 1.954634800 0.442060500 0.131273400 0.88 0.982329400 1.938466900 0.443409200 0.138459200 0.89 1.001632700 1.922158200 0.444829900 0.145707500 0.90 1.020772100 1.905716900 0.446323500 0.153014700 0.91 1.039746600 1.889151000 0.447890400 0.160377300 0.92 1.058554800 1.872468700 0.449531200 0.167791700 0.93 1.077195600 1.855677800 0.451246400 0.175254300 0.94 1.095668000 1.838786200 0.453036400 0.182761700 0.95 1.113971000 1.821801900 0.454901800 0.190310300 0.96 1.132103700 1.804732600 0.456842800 0.197896600 0.97 1.150065400 1.787586100 0.458859800 0.205517300 0.98 1.167855200 1.770369900 0.460953200 0.213168900 0.99 1.185472600 1.753091700 0.463123300 0.220848100 |
В качестве интервала [Left;
Right] возьмем интервал
[0.2; 0.6]. На нем
,
а минимальное и максимальное значения
производной примем равными M=2.5,
m=2.2. Начальное приближение
корня x0=0.6.