Лабораторная работа 5
.docФедеральное агенство по образованию РФ
СПбГЭТУ «ЛЭТИ»
Кафедра МО-ЭВМ
Факультет КТИ
ОТЧЕТ
по лабораторной работе № 5
Метод Ньютона.
Дисциплина: вычислительная мпатематика
Студент группы 4351
Кузьменко А.
Преподаватель:
Щеголева Н.Л.
Санкт-Петербург
2006
Лабораторная работа № 5
Метод Ньютона.
1. Постановка задачи.
Найти
корень уравнения
для функции
с заданной точностью Eps
методом Ньютона, исследовать скорость
сходимости и обусловленность метода.
2. Теоретические сведения.
В
случае, когда известно хорошее начальное
приближение решения уравнения
,
эффективным методом повышения точности
является метод Ньютона. Он состоит в
построении итерационной последовательности
сходящейся к корню уравнения
.
Для того, чтобы последовательность сходилась, накладываются следующие ограничения на интервал, из которого выбирается начальное приближение: f (x) и f (x) должны сохранять определенные знаки и для начального приближения x0 f(x0)f (x0)>0.
Метод
Ньютона допускает простую геометрическую
интерпретацию (рис. 3.2). Если через точку
с координатами
провести касательную, то координата
точки пересечения этой касательной с
осью абсцисс будет очередным приближением
xn
+1
корня
уравнения
.
Для
оценки погрешности n-го
приближения корня предлагается
пользоваться неравенством
где
М2
- наибольшее значение модуля второй
производной
на отрезке (a,
b);
m1
- наименьшее значение модуля первой
производной
на отрезке (a,
b).
3. Текст программ.
double NEWTON (double X,double Eps,int &N)
{
extern double F1 (double);
double Y,Y1,DX;
N=0;
do
{
Y = F(X);
if (Y==0.0) return (X);
Y1 = F1(X);
if (Y1==0.0) {puts("производная обратилась в 0\n");getch();exit(1);}
printf("x=%f \n",X);
DX=Y/Y1; X=X-DX; N++;
if (N>30) DX=Eps;
}
while (fabs(DX)>Eps);
return (X);
}
#include "methods.h"
double delta;
void main()
{
int k;
long int s;
float eps1,delta1,a1;
double eps,x0,x;
printf("введите delta:");
scanf("%f",&delta1);
delta = delta1;
printf("введите eps:");
scanf("%f",&eps1);
eps = eps1;
printf("введите x0:");
scanf("%f",&a1);
x0 = a1;
x = NEWTON (x0,eps,k);
printf("x=%f k=%d\n",x,k);
getch();
}
double F(double x)
{
extern double delta;
double s;
if (x==0) {printf ("деление на 0!"); getch(); exit(1);}
{ s = (pow(x,4))-(13*(x*x))+36-(1/x);
s = Round( s,delta );
return(s);
}
}
double F1(double x)
{
extern double delta;
double s;
if (x==0) {printf (" деление на 0!"); getch(); exit(1);}
{ s = (4*pow(x,3))-(26*x)+(1/(x*x));
s = Round (s,delta);
return(s);
}
}
4. Вычислительный эксперимент.
Функция f(x)=x4-13x2+36-1/x имеет следующий вид:
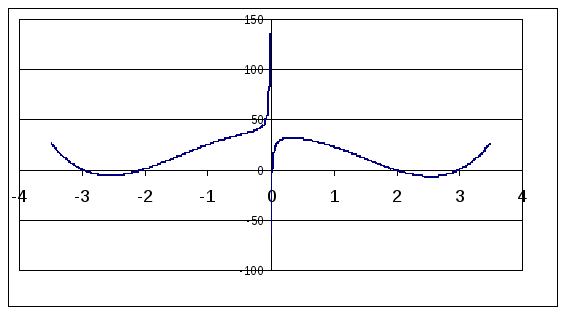
Для каждого из 5 корней уравнения f(x)=0 необходимо найти интервалы, из которых можно выбирать начальное приближение для использования метода Ньютона. Метод будет сходиться на следующих интервалах:
(-; -2.56), (-2.49; -0.59), (10-4; 0.05), (0.76; 2.46), (2.55; +).
Таким образом, выбрав из этих интервалов начальные приближения, найдем методом Ньютона корни уравнения с различной точностью.
Например, пусть x01=-3.5, x02=-1.5, x03=0.02, x04=1.5, x05=3.5, delta=0.000001. Тогда:
-
eps
x1
k1
x2
k2
x3
k3
x4
k4
x5
k5
0,1
-2,989921
3
-2,024007
2
0,025603
1
1,974593
2
3,01174
3
0,01
-2,988674
4
-2,025041
3
0,025603
1
1,975021
3
3,010909
4
0,001
-2,988672
5
-2,025042
4
0,027784
3
1,975021
3
3,010909
4
0,0001
-2,988672
5
-2,025042
4
0,027786
4
1,975021
4
3,010908
5
0,00001
-2,988672
5
-2,025042
4
0,027786
4
1,975021
4
3,010908
5
0,000001
-2,988672
5
-2,025042
4
0,027786
5
1,975021
4
3,010908
5
Исследуем
сходимость метода, для этого рассмотрим
задачу нахождения корня x5.
Согласно теории, верно неравенство:
где М2
= max
,
m1
=min
на отрезке (a,
b),
что говорит о квадратичной сходимости
метода.
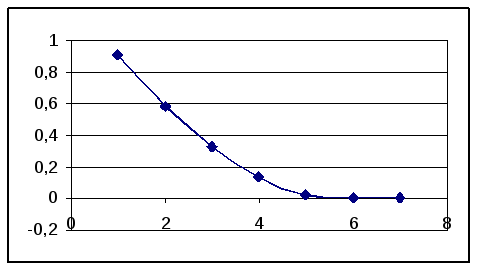
Рассмотрим интервал (3, 5): на нем m1=f (3)=30.1111, M2=f (5)=273.984. Возьмем delta=0,000001, eps=0.0001, x0=5. В таблице отражены все итерации метода и на каждом шаге вычислена теоретическая верхняя граница величины интервала по величине предыдущего. На графике - зависимость величины интервала от шага метода.
|
n |
xn |
(xn - xn-1)теор |
(xn - xn-1)практ |
|
|
0 |
5 |
|
|
|
|
1 |
4,092531 |
18,19819927 |
0,907469 |
|
|
2 |
3,505381 |
3,746554211 |
0,58715 |
|
|
3 |
3,173472 |
1,568435109 |
0,331909 |
|
|
4 |
3,0372903 |
0,501194715 |
0,1361817 |
|
|
5 |
3,011788 |
0,084373473 |
0,0255023 |
|
|
6 |
3,010909 |
0,002958878 |
0,000879 |
|
|
7 |
3,010908 |
3,51517E-06 |
1E-06 |
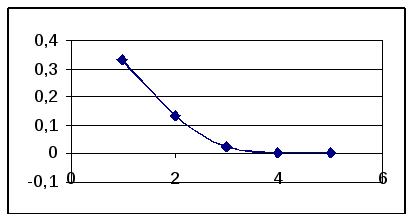
Видно, что верхняя граница дает весьма неточное приближение. Рассмотрим меньший интервал (3, 3.5): на нем m1=f (3)=30.1111, M2=f (3,5)=120.953.
Возьмем delta=0,000001, eps=0.00001, x0=3,5. Получим:
|
n |
xn |
(xn - xn-1)теор |
(xn - xn-1)практ |
|
|
0 |
3,5 |
|
|
|
|
1 |
3,170809 |
0,502111163 |
0,329191 |
|
|
2 |
3,03654 |
0,217648548 |
0,134269 |
|
|
3 |
3,01174 |
0,03620857 |
0,0248 |
|
|
4 |
3,010909 |
0,001235274 |
0,000831 |
|
|
5 |
3,010908 |
1,38695E-06 |
1E-06 |
В этом случае теоретическая формула дает лучшее приближение.
Рассмотрим обусловленность метода на примере этого же корня. Так как известна функция, то можно вычислить число обусловленности задачи нахождения простого корня этой функции (1/|f (x0)|, где x0 - корень). Для данных функции и корня =0,03225. Рассматриваются различные варианты обусловленности задачи и исходные приближения корня.
В столбце “теоретически” вычисляется отношение eps/delta и выводится “да”, если меньше его и “нет” в обратном случае. В столбце “практически” вычисляется разность найденного значения x и эталона (значения корня с наименьшей погрешностью) и выводится “да”, если это значения меньше заданной точности результата (eps). В результате получим:
|
x0 |
eps |
delta |
x |
теоретически |
практически |
||
|
3,5 |
1E-08 |
1E-08 |
3,010908 |
eps/delta |
обусл |
погр y |
соотв |
|
10 |
0,0001 |
0,01 |
3,010938 |
0,01 |
нет |
3E-05 |
да |
|
8 |
0,005 |
0,5 |
3,004502 |
0,01 |
нет |
0,006406 |
нет |
|
5 |
0,001 |
0,1 |
3,012179 |
0,01 |
нет |
0,001271 |
нет |
|
3,2 |
0,1 |
5 |
3,1 |
0,02 |
нет |
0,089092 |
да |
|
3,5 |
0,00001 |
0,0005 |
3,010909 |
0,02 |
нет |
1E-06 |
да |
|
4 |
0,001 |
0,05 |
3,010923 |
0,02 |
нет |
1,5E-05 |
да |
|
3,5 |
0,0005 |
0,0167 |
3,011021 |
0,03 |
нет |
0,000113 |
да |
|
10 |
0,01 |
0,3333 |
3,016199 |
0,03 |
нет |
0,005291 |
да |
|
3,9 |
0,0001 |
0,0025 |
3,010878 |
0,04 |
да |
3E-05 |
да |
|
10 |
0,005 |
0,125 |
3,010229 |
0,04 |
да |
0,000679 |
да |
|
3,4 |
0,001 |
0,025 |
3,010814 |
0,04 |
да |
9,4E-05 |
да |
|
5 |
0,1 |
2 |
3,030732 |
0,05 |
да |
0,019824 |
да |
|
3,5 |
0,000005 |
0,0001 |
3,010906 |
0,05 |
да |
2E-06 |
да |
|
9 |
0,001 |
0,02 |
3,011075 |
0,05 |
да |
0,000167 |
да |
|
100 |
0,0005 |
0,01 |
3,010791 |
0,05 |
да |
0,000117 |
да |
|
3,1 |
0,01 |
0,2 |
3,00978 |
0,05 |
да |
0,001128 |
да |
|
4,5 |
0,001 |
0,02 |
3,010713 |
0,05 |
да |
0,000195 |
да |
5. Выводы.
Для применения метода Ньютона необходимо найти интервал, удовлетворяющий условию сходимости метода, что требует некоторых усилий (по сравнению с методом бисекций и методом хорд), но метод Ньютона в отличие от этих методов имеет квадратичную, а не линейную сходимость. Однако метод Ньютона может сходиться довольно медленно при малом значении производной функции близ корня (малой крутизне графика).
При хорошей обусловленности задачи метод Ньютона, также как и методы хорд и бисекций дает результат, соответствующий требуемой точности, при плохой обусловленности задачи точность результата в некоторых случаях меньше требуемой.
Сходимость метода бисекций и хорд зависит только от длины интервала и требуемой точности. В методе Ньютона также важно, насколько удачно выбрано первое приближение.
Таким образом, метод Ньютона менее универсальный (накладывает серьезные ограничения на функцию и интервал), но сходится гораздо быстрее методов хорд и бисекций.