Лабораторная работа 10
.docФедеральное агенство по образованию РФ
СПбГЭТУ «ЛЭТИ»
Кафедра МО-ЭВМ
Факультет КТИ
ОТЧЕТ
по лабораторной работе № 10
Интерполяционные формулы для равноотстоящих узлов.
Дисциплина: вычислительная мпатематика
Студент группы 4351
Кузьменко А.
Преподаватель:
Щеголева Н.Л.
Санкт-Петербург
2006
Лабораторная работа № 10
Интерполяционные формулы для равноотстоящих узлов.
1. Постановка задачи.
Разработать программу, обеспечивающую вычисление значения функции в заданных точках с использованием подходящих для каждого конкретного случая интерполяционных формул.
Вычислить в точках x1=1.4980, x2= 0.4120, x3= 1.6840 значения функции, заданной таблицей, для узлов с равноотстоящим шагом:
-
X[ 0] = 0.2930
Y[ 0] = -0.2540
X[ 1] = 0.4690
Y[ 1] = -0.0630
X[ 2] = 0.6460
Y[ 2] = 0.0150
X[ 3] = 0.8220
Y[ 3] = 0.0130
X[ 4] = 0.9980
Y[ 4] = -0.0360
X[ 5] = 1.1740
Y[ 5] = -0.1010
X[ 6] = 1.3510
Y[ 6] = -0.1470
X[ 7] = 1.5270
Y[ 7] = -0.1420
X[ 8] = 1.7030
Y[ 8] = -0.0540
X[ 9] = 1.8790
Y[ 9] = 0.1500
X[10] = 2.0560
Y[10] = 0.5060
2. Теоретические сведения.
Если
значения функции
заданы в точках
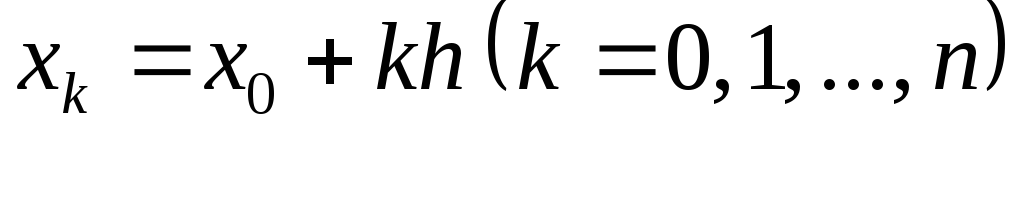с постоянным положительным шагом, то
часто используется интерполяционный
многочлен Ньютона для интерполяции
вперед
,
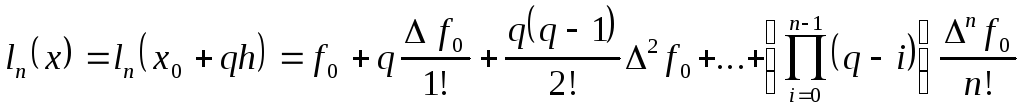(1.10)
где
,
а конечные разности
,
носящие
названия нисходящих разностей, находят
из соотношений
,
.
Интерполяционный
многочлен (1.10) удобно использовать при
работе в начале таблицы значений функции
и для экстраполяции левее точки
.
Интерполяционный
многочлен с узлами
где
,
имеет вид
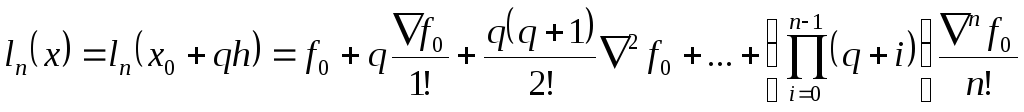(1.11)
и
называется интерполяционным многочленом
Ньютона для интерполяции назад. Его
удобно использовать при интерполяции
в конце таблицы и для экстраполяции
правее точки
.
Входящие в выражение (1.11) значения
конечных восходящих разностей находят
из соотношений
,
... ,
.
Если
при заданном
в таблице значений функции
с шагом
имеется достаточное число узлов с каждой
стороны от
,
то целесообразно узлы интерполяции
выбрать так, чтобы точка
оказалась как можно ближе к середине
минимального отрезка, содержащего узлы.
При этом обычно в качестве
берется ближайший к
узел, затем за
принимается ближайший к
узел, расположенный с противоположной
от
стороны, чем
.
Следующие узлы назначаются поочередно
с разных сторон от
и должны быть расположены как можно
ближе к
.
Одной из возможных схем интерполяции
в этом случае является схема Стирлинга
с интерполяционным многочленом вида
В
этом выражении учитывается, что дано
нечетное число
значений функции
,
где
.
Обычно эту формулу целесообразно
использовать при
.
3. Текст программ.
# include <iostream.h>
# include <math.h>
# include <conio.h>
# include <stdlib.h>
const n=10;
double x[n+1] = {0.2930, 0.4690, 0.6450, 0.8210, 0.9970, 1.1730, 1.3490, 1.5250, 1.7010, 1.8770, 2.0530};
double y[n+1] = {-0.2540, -0.0630, 0.0150, 0.0130, -0.0360, -0.1010, -0.1470, -0.1420, -0.0540, 0.1500, 0.5060};
double z[3]={1.4980, 1.6840, 0.4120};
double delt(int, int);
double Newt_F(double);
double Newt_B(double);
double Stirl(int, double);
void main()
{
int i,j,d ; double mn,b,q;
for (i=0;i<3;i++)
{ b=z[i];
cout<<"\n\n***Программа вычисляет значение в точке x["<<i+1
<<"] = "<<b<<" *** ";
mn=10000;
for (j=1;j<=n;j++)
{
if (fabs(x[j]-b)<mn)
{ mn=fabs(x[j]-b);
d=j;
}
}
if ((d>(n-4)/2) & (d<=(n+4)/2) & (mn/(x[2]=x[1])<0.25))
{ q=fabs(b-x[d])/(x[1]-x[0]);
cout<<"\n Расчет ведется метолом Стирлинга "
<<"\n Результат: "<<Stirl(d,q);
}
else
if ((n-d)>n/2)
{ q=(b-x[0])/(x[1]-x[0]);
cout<<"\n Расчет ведется методом Ньютона для интерполяции вперед"
<<"\n Результат: "<<Newt_F(q);
}
else
{ q=(-x[n]+b)/(x[1]-x[0]);
cout<<"\n Расчет ведется методом Ньютона для интерполяции назад"
<<"\n Результат: "<<Newt_B(q);
};
}
getch();
}
double delt(int m, int k)
{
double d;
if (m==1) { d=y[k+1]-y[k]; }
else { d=delt(m-1,k+1)-delt(m-1,k); }
return d;
};
double Newt_F(double q)
{
double S,Q,p; int i;
Q=1; S=y[0];p=1;
for (i=1;i<=n;i++)
{
Q=Q*(q-i+1);
p=p*i;
S=S+(Q/p)*delt(i,0);
}
return (S);
}
double Newt_B(double q)
{
double S,Q,p; int i;
Q=1; S=y[n]; p=1;
for (i=1;i<=n;i++)
{
Q=Q*(q+i-1);
p=p*i;
S=S+(Q/p)*delt(i,n-i);
}
return (S);
}
double Stirl(int d, double q)
{
double S,Q=1,p1=1, p2=1; int t,i;
if (d>(n-d)) {t=n-d;} else {t=d;}
S=y[d];
for (i=1;i<=t;i++)
{
p1=p2*(2*i-1); p2=p1*2*i;
S=S+(q*Q/p1)*(delt(2*i-1,t-i)+delt(2*i-1,t-i+1))/2;
S=S+((q*q)*Q/p2)*delt(2*i,t-i);
Q=Q*(q*q-i*i);
}
return S;
}
4. Вычислительный эксперимент.
После выполнения программы экран имеет вид:
***Программа вычисляет значение в точке x[1] = 1,498 ***
Расчет ведется метолом Стирлинга
Результат: -0,147251
***Программа вычисляет значение в точке x[2] = 1,684 ***
Расчет ведется методом Ньютона для интерполяции назад
Результат: -0,067078
***Программа вычисляет значение в точке x[3] = 0,412 ***
Расчет ведется методом Ньютона для интерполяции вперед
Результат: -0,112833
Построим график функции по заданным значениям в узлах и обозначим найденные точки для визуальной оценки результата:
5. Выводы.
Написанная программа позволяет вычислять значения неизвестной или трудновычислимой функции, если известен ряд ее значений в узлах интерполяции, отстоящих друг от друга на равном расстоянии (интерполяция с постоянным шагом). При этом точка, в которой производятся вычисления, должна лежать в пределах минимального отрезка, охватывающего все узлы интерполяции, иначе речь идет об экстраполяции и точность вычислений резко снижается.
Представленная программа позволяет производить вычисления по наиболее подходящей формуле. Формулы Ньютона для интерполирования вперед и назад подходят для вычисления значение функции в точке, близкой к началу или к концу минимального интервала, содержащего все узлы интерполяции. Формула Стирлинга применяется, если точка в центре интервала и |q|<0.25.
Расчет по формулам Ньютона и Стирлинга предполагает довольно трудоемкое ("вручную") вычисление нисходящих (или восходящих) разностей, поэтому программирование этого алгоритма представляет практический интерес.
К сожалению, в условиях данной задачи (вид функции неизвестен) сложно оценить точность вычисления значения функции, но визуальная оценка подтверждает правильность вычислений.