Лабораторная работа 4
.docФедеральное агенство по образованию РФ
СПбГЭТУ «ЛЭТИ»
Кафедра МО-ЭВМ
Факультет КТИ
ОТЧЕТ
по лабораторной работе № 4
Метод хорд.
Дисциплина: вычислительная мпатематика
Студент группы 4351
Кузьменко А.
Преподаватель:
Щеголева Н.Л.
Санкт-Петербург
2006
Лабораторная работа № 4
Метод хорд.
1. Постановка задачи.
Найти
корень уравнения
для функции
с
заданной точностью Eps
методом хорд, исследовать скорость
сходимости и обусловленность метода.
2. Теоретические сведения.
Пусть
найден отрезок (a,
b),
на котором функция
меняет знак. Для определенности примем
(a)
> 0,
(b)
< 0. В
методе хорд процесс итераций состоит
в том, что в качестве приближений к
значению корня уравнения
принимаются значения c0,
c1,
. . . , cn
точек
пересечения хорды с осью абсцисс, как
это показано на рис.3.1.
Сначала решается уравнение хорды АВ:
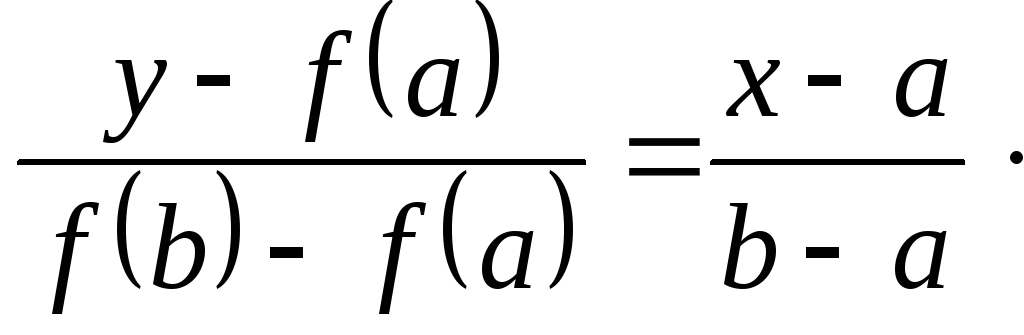
Для нахождения точки пересечения ее с осью абсцисс (x = c0, y = 0) используется уравнение
Далее
сравниваются знаки величин
(a)
и
(с0)
и для рассматриваемого случая оказывается,
что корень находится в интервале (a,
c0),
так как
(a)
(с0)
< 0. Отрезок
(c0,
b)
отбрасывается. Следующая итерация
состоит в определении нового приближения
c1
как точки пересечения хорды АВ1
с осью абсцисс и т. д. Итерационный
процесс продолжается до тех пор, пока
значение
(cn)
не станет по модулю меньше заданного
числа
(см. 3.1).
3. Текст программ.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include "methods.h"
#include <conio.h>
#include <iostream.h>
double delta;
void main()
{
int k;
long int s;
float eps1,delta1,a1,b1;
double eps,a,b,x;
printf("введите delta:");
scanf("%f",&delta1);
delta = delta1;
printf("введите eps:");
scanf("%f",&eps1);
eps = eps1;
printf("введите a:");
scanf("%f",&a1);
a = a1;
printf("введите b:");
scanf("%f",&b1);
b = b1;
x = HORDA(a,b,eps,k);
printf("x=%f k=%d\n",x,k);
getch();
}
double F(double x)
{
extern double delta;
double s;
if (x==0) {printf ("Деление на 0!"); getch(); exit(1);}
{ s = (pow(x,4))-(13*(x*x))+36-(1/x);
s = Round( s,delta );
return(s);
}
}
double HORDA(double Left,double Right,double Eps,int &N)
{
double FLeft = F(Left);
double FRight = F(Right);
double X,Y;
if (FLeft*FRight>0.0)
{puts("Неверное задание интервала\n");getch();exit(1);}
if (Eps<=0.0)
{puts("Неверное задание точности\n");getch();exit(1);}
N=0;
if (FLeft==0.0) return Left;
if (FRight==0.0) return Right;
do
{
X = Left-(Right-Left)*FLeft/(FRight-FLeft);
Y = F(X);
if (Y == 0.0) return (X);
if (Y*FLeft < 0.0)
{ Right=X; FRight=Y; }
else
{ Left=X; FLeft=Y; }
N++;
}
while ( fabs(Y) >= Eps );
return(X);
}
4. Вычислительный эксперимент.
Для вычисления простых корней уравнения необходимо сначала их изолировать, то есть определить интервалы, в которых находятся только по одному корню. Уравнение f(x)=x4-13x2+36-1/x имеет 5 корней. График функции:
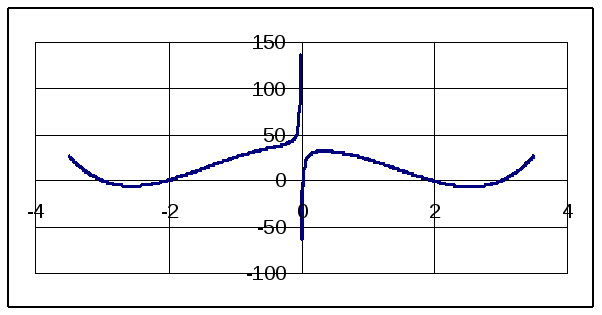
Таким образом, если изолировать корни уравнения, получим 5 интервалов:
(-3, -2.9), (-2.1, -2), (0.02, 0.03), (1.9, 2), (3, 3.1)
Ниже приведена таблица, в которой отражены результаты работы программы, вычисляющей корни уравнения с определенной точностью методом хорд. (Здесь x1 – корень из интервала (-3, -2.9), x2 – из (-2.1, -2), x3 – из (0.02 , 0.03). x4 – из (1.9, 2), x5 – из (3, 3.1))
|
eps |
delta |
x1 |
k1 |
x2 |
k2 |
x3 |
k3 |
x4 |
k4 |
x5 |
k5 |
|
0,1 |
0,000001 |
-2,987132 |
1 |
-2,026237 |
1 |
0,027851 |
16 |
1,975913 |
1 |
3,00971 |
1 |
|
0,05 |
0,000001 |
-2,987132 |
1 |
-2,026237 |
1 |
0,027813 |
18 |
1,975913 |
1 |
3,00971 |
1 |
|
0,01 |
0,000001 |
-2,988648 |
2 |
-2,025059 |
2 |
0,027793 |
21 |
1,975052 |
2 |
3,010777 |
2 |
|
0,001 |
0,000001 |
-2,988648 |
2 |
-2,025059 |
2 |
0,027786 |
26 |
1,975052 |
2 |
3,010894 |
3 |
|
0,0001 |
0,000001 |
-2,988672 |
3 |
-2,025042 |
3 |
0,027786 |
32 |
1,975022 |
3 |
3,010906 |
4 |
|
0,00001 |
0,000001 |
-2,988672 |
3 |
-2,025042 |
3 |
0,027786 |
37 |
1,975021 |
3 |
3,010908 |
5 |
|
0,000001 |
0,000001 |
-2,988672 |
3 |
-2,025042 |
3 |
0,027786 |
43 |
1,975021 |
3 |
3,010908 |
5 |
Следующая таблица отображает зависимость количества итераций (k) метода хорд от требуемой точности результата (eps):
|
eps |
x |
k |
|
|
|
5 |
0,031426 |
7 |
|
|
|
1 |
0,028397 |
11 |
|
|
|
0,5 |
0,028036 |
13 |
|
|
|
0,1 |
0,027851 |
16 |
|
|
|
0,05 |
0,027813 |
18 |
|
|
|
0,01 |
0,027793 |
21 |
|
|
|
0,005 |
0,027788 |
23 |
|
|
|
0,001 |
0,027786 |
26 |
|
|
|
0,0005 |
0,027786 |
28 |
|
|
|
0,0001 |
0,027786 |
32 |
|
|
|
0,00005 |
0,027786 |
33 |
|
|
|
0,00001 |
0,027786 |
37 |
|
|
|
0,000005 |
0,027786 |
39 |
|
|
|
0,000001 |
0,027786 |
43 |
|
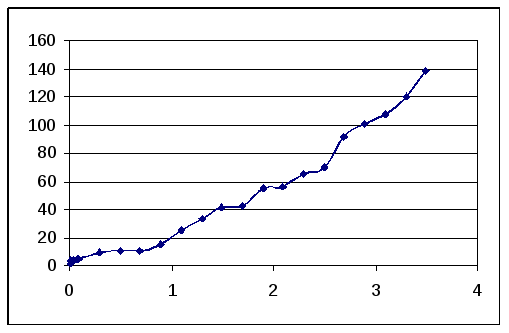
Также количество итераций зависит от длины интервала, локализующего корень:
|
a |
b |
|a-b| |
k |
|
|
|
3 |
3,011 |
0,011 |
1 |
|
|
|
3 |
3,02 |
0,02 |
3 |
|
|
|
3 |
3,05 |
0,05 |
4 |
|
|
|
3 |
3,08 |
0,08 |
5 |
|
|
|
3 |
3,1 |
0,1 |
5 |
|
|
|
2,9 |
3,2 |
0,3 |
9 |
|
|
|
2,7 |
3,2 |
0,5 |
10 |
|
|
|
2,5 |
3,2 |
0,7 |
10 |
|
|
|
2,5 |
3,4 |
0,9 |
15 |
|
|
|
2,7 |
3,8 |
1,1 |
25 |
|
|
|
2,8 |
4,1 |
1,3 |
33 |
|
|
|
2,9 |
4,4 |
1,5 |
41 |
|
|
|
3 |
4,7 |
1,7 |
42 |
|
|
|
2,8 |
4,7 |
1,9 |
55 |
|
|
|
2,5 |
4,6 |
2,1 |
56 |
|
|
|
2,5 |
4,8 |
2,3 |
65 |
|
|
|
3 |
5,5 |
2,5 |
70 |
|
|
|
2,9 |
5,6 |
2,7 |
92 |
|
|
|
2,7 |
5,6 |
2,9 |
101 |
|
|
|
2,5 |
5,6 |
3,1 |
107 |
|
|
|
2,5 |
5,8 |
3,3 |
120 |
|
|
|
2,7 |
6,2 |
3,5 |
138 |
|
Следующая таблица содержит результаты нахождения корня уравнения в рамках исследования чувствительности метода к ошибкам во входных данных.
Рассматриваются интервалы разной длины, содержащие корень 1.975021. Так как известна функция, то можно вычислить число обусловленности задачи нахождения простого корня этой функции (1/|f (x0)|, где x0 - корень). Для данных функции и корня =0,04931. В столбце “теоретически” вычисляется отношение eps/delta и выводится “да”, если меньше его и “нет” в обратном случае. В столбце “практически” вычисляется разность найденного значения x и эталона (значения корня с наименьшей погрешностью) и выводится “да”, если это значения меньше заданной точности результата (eps)
-
a
b
eps
delta
x
теоретически
практически
1,9
2
1E-08
1E-08
1,975021
eps/delta
обусл
погр f(x)
соотв
1,9
2
0,001
0,1
1,97619
0,01
нет
0,001169
нет
1,5
2,5
0,001
0,1
1,974928
0,01
нет
9,3E-05
да
1
3
0,001
0,1
1,973723
0,01
нет
0,001298
нет
0,1
2
0,001
0,1
1,974297
0,01
нет
0,000724
да
-1
3
0,001
0,1
1,975128
0,01
нет
0,000107
да
-2
3
0,001
0,1
1,976966
0,01
нет
0,001945
нет
1,9
2
0,01
0,25
1,975
0,04
нет
2,1E-05
да
1
3
0,01
0,25
1,978472
0,04
нет
0,003451
да
-2
3
0,01
0,25
1,975246
0,04
нет
0,000225
да
1,9
2
0,001
0,02
1,975012
0,05
да
9E-06
да
1,5
2,5
0,001
0,02
1,975202
0,05
да
0,000181
да
1
3
0,001
0,02
1,975161
0,05
да
0,00014
да
0,1
2
0,001
0,02
1,974992
0,05
да
2,9E-05
да
-1
3
0,001
0,02
1,974615
0,05
да
0,000406
да
-2
3
0,001
0,02
1,975383
0,05
да
0,000362
да
5. Вывод.
Метод хорд является универсальным методом нахождения простых корней уравнений вида f(x)=0, то есть метод дает результат при любых условиях, если локализован искомый корень. При этом при применении метода хорд в ряде случаев количество итераций меньше, чем при применении метода бисекций.
Количество итераций метода хорд зависит от:
1) требуемой точности корня: чем выше точность, тем больше итераций;
2) длины интервала локализации: чем больше интервал, тем больше итераций;
3) от угла наклона касательной к графику в точке x=0: чем круче график, тем больше итераций. То есть число итераций при прочих равных условиях зависит от первой производной функции |f (x0)|, где x0 – корень уравнения f (x)=0.
При нахождении корня методом хорд можно гарантировать соответствие корня требуемой точности, если задача хорошо обусловлена, то есть если eps/delta . При этом, даже если это условие не выполняется (при не очень большом несоответствии), точность корня, найденного методом хорд довольно высока и нередко соответствует требуемой точности.