Лабораторная работа 9
.docФедеральное агенство по образованию РФ
СПбГЭТУ «ЛЭТИ»
Кафедра МО-ЭВМ
Факультет КТИ
ОТЧЕТ
по лабораторной работе № 9
Интерполяционные формулы для неравноотстоящих узлов.
Дисциплина: вычислительная мпатематика
Студент группы 4351
Кузьменко А.
Преподаватель:
Щеголева Н.Л.
Санкт-Петербург
2006
Лабораторная работа № 9
Интерполяционные формулы для неравноотстоящих узлов.
1. Постановка задачи.
Используя интерполяционную схему Эйткена либо интерполяционную формулу Ньютона, вычислить значение в точке x = 4,7296 функции, заданной таблицей (значений функции в узлах X[ i] ).
-
X[ 0] = 0.5016
Y[ 0] = -1.8658
X[ 1] = 1.2472
Y[ 1] = 0.3262
X[ 2] = 2.4400
Y[ 2] = -0.3548
X[ 3] = 2.5432
Y[ 3] = -0.3829
X[4] = 2.9296
Y[ 4] = -0.1263
X[ 5] = 2.9584
Y[ 5] = -0.0781
X[ 6] = 3.2336
Y[ 6] = 0.6437
X[ 7] = 3.2944
Y[ 7] = 0.8743
X[ 8] = 3.9368
Y[ 8] = 5.3285
X[ 9] = 5.7816
Y[ 9] = 50.2972
X[10] = 6.0488
Y[10] = 62.3223
2. Теоретические сведения.
Пусть
известны значения некоторой функции
в n+1
различных точках
,
которые обозначим следующим образом:
.
В
задаче интерполяции
функции
решается проблема приближенного
восстановления значения функции в
произвольной точке x.
Для этого строится алгебраический
многочлен
степени n,
который в точках
принимает заданные значения, т. е.
.
В общем случае доказано, что существует единственный интерполяционный многочлен n-й степени, удовлетворяющий условиям (1.4),
,
(1.5)
где
.
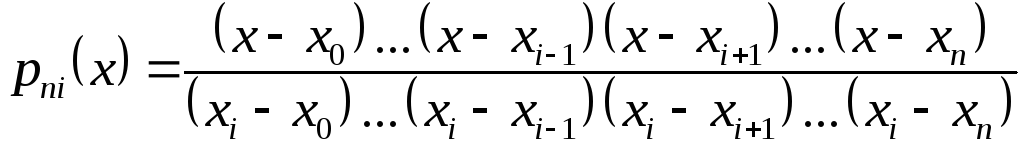(1.6)
Интерполяционный многочлен, представленный в виде (1.5), называется интерполяционным многочленом Лагранжа, а функции (1.6) - лагранжевыми коэффициентами [1]-[4].
Для
оценки погрешности интерполяции в
текущей точке
(
- отрезок, содержащий все узлы интерполяции
и точку x)
можно использовать соотношение
,
(1.7)
где
;
-
(n+1)-я
производная интерполируемой функции
в некоторой точке
;
.
Интерполяционный многочлен Ньютона для неравноотстоящих узлов интерполяции имеет вид
…
…
,
(1.9)
где
- разделенная разность k-го
порядка.
Вычисление разделенных разностей производится по соотношениям
,
...................................................
.
При использовании интерполяционного многочлена Ньютона (1.9) изменение степени n требует только добавить или отбросить соответствующее число стандартных слагаемых, что удобно на практике. В то же время, непосредственное использование интерполяционного многочлена Лагранжа (1.5) требует строить его заново при изменении n.
В
том случае, если требуется найти лишь
численное значение интерполяционного
многочлена
,
а не его представление, может быть
использована итерационно-интерполяционная
схема Эйткена [6], [12].
Пусть
- интерполяционный многочлен, определяемый
парами
,
,
,
... так, что
.
Интерполяционные многочлены возрастающих степеней получают последовательно следующим образом:
,
,
...…..............................................
,
......................................................
.
......................................................
Этот процесс можно закончить, когда у значений двух интерполяционных многочленов последовательных степеней совпадает требуемое количество знаков.
3. Текст программ.
# include <iostream.h>
# include <math.h>
# include <conio.h>
const n=11;
double x[n]={0.5016,1.2472,2.4400,2.5432,2.9296,2.9584,3.2336,3.2944,3.9368,5.7816,6.0488};
double y[n]={-1.8658,0.3262,-0.3548,-0.3829,-0.1263,-0.0781,0.6437,0.8743,5.3285,50.2972,62.3223};
double z=4.7296;
double f(int, int);
double Interp_N() ;
double Eit(int ,int);
void main()
{
cout<<"\n***Программа вычисляет значение в точке x=4.7296 *** "
<<"\n\n--- интерполяционного многочлена Ньютона ---"
<<"\n\n Результат: "<<Interp_N()
<<"\n\n--- по интерполяционной формуле Эйткена ---"
<<"\n\n Резудьтат: "<<Eit(11,11);
getch();
}
double f(int m, int l)
{
double s;
if (m==0) { s=y[0]; }
else { if (m==1) { s=(y[l+1]-y[l])/(x[l+1]-x[l]); }
else { s=(f(m-1,l+1)-f(m-1,l))/(x[l+m]-x[l]); }
}
return s;
}
double Eit(int n,int m)
{
double s;
if (n==0) {s=y[m];}
else
{ s=((z-x[m-n])*Eit(n-1,m)-(z-x[m])*Eit(n-1,m-1))/(x[m]-x[m-n]); }
return (s);
}
double Interp_N()
{
int i,j; double s,p;
s=0;
for (i=0;i<n;i++)
{
p=1;
for (j=0;j<i;j++)
{
p=p*(z-x[j]);
}
s=s+p*f(i,0);
}
return s;
}
4. Вычислительный эксперимент.
После выполнения программы экран имеет вид:
*** Программа вычисляет значение в точке x=4.7296 ***
--- интерполяционного многочлена Ньютона ---
Результат: 17,945457
--- по интерполяционной формуле Эйткена ---
Резудьтат: 17,945457
Построим график функции по заданным значениям в узлах и обозначим найденные точки для визуальной оценки результата:
5. Выводы.
Оба метода вычисления значения интерполяционного многочлена в точке, отличной от узлов интерполяции, дали один и тот же результат, что свидетельствует об отсутствии ошибок в процессе вычисления.
Написанная программа позволяет вычислять значения неизвестной или трудновычислимой функции, если известен ряд ее значений в узлах интерполяции. при этом точка, в которой производятся вычисления должна лежать в пределах минимального отрезка, охватывающего все узлы интерполяции, иначе речь идет об экстраполяции и точность вычислений резко снижается.
К сожалению, в условиях данной задачи (вид функции неизвестен) сложно оценить точность вычисления значения функции.