Сложение колебаний одинаковой

частоты и направления:

амплитуда результирующего

колебания ,

где А₁ и А₂ – амплитуды составляющих колебаний,

₁ и ₂ – начальные фазы составляющих колебаний;

начальная фаза результирующего

колебания .

Уравнение затухающих колебаний: ,

е = 2,71… – основание натуральных логарифмов.

Амплитуда затухающих колебаний: ,

где – амплитуда в начальный момент времени;

 – коэффициент затухания;

t – время.

Коэффициент затухания:

колеблющегося тела ,

где r – коэффициент сопротивления среды,

m – масса тела;

колебательного контура ,

где R – активное сопротивление,

L – индуктивность контура.

Частота затухающих колебаний : .

Период затухающих колебаний Т: .

Логарифмический декремент затухания: .

Связь логарифмического декремента  и коэффициента

затухания : .

Амплитуда вынужденных колебаний ,

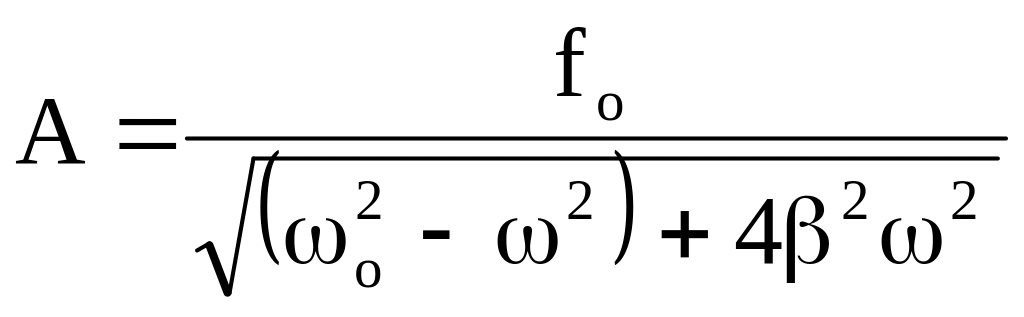где  – частота вынужденных колебаний,

f_о – приведенная амплитуда вынуждающей силы,

при механических колебаниях: ,

при электромагнитных колебаниях: .

Резонансная частота .

Резонансная амплитуда .

Полная энергия колебаний: .

Уравнение плоской волны:

где  – смещение точек среды с координатой х

в момент времени t;

k – волновое число: .

Длина волны: ,

где v – скорость распространения колебаний в среде,

Т – период колебаний.

Связь разности фаз  колебаний двух точек

среды с расстоянием х между точками среды: .

7.3.3. Примеры решения задач по колебаниям и волнам

Задача 1. Материальная точка массой 10 г совершает гармоническое колебание с периодом Т=1 с. Определить амплитуду колебаний, максимальную скорость и ускорение колеблющейся точки, если полная энергия точки равна 0,02 Дж.

Дано:

Найти:

Решение: Уравнение гармонического колебания запишем в виде:

, (1)

где х – смещение материальной точки от положения равновесия;

А – амплитуда;

 – циклическая (круговая) частота;

t – время;

 – начальная фаза.

Скорость колеблющейся точки среды определяется как первая производная от смещения по времени:

.

Максимальное значение скорости: .

Ускорение точки определяется как производная от скорости по времени:

.

Максимальное значение ускорения: .

Полная энергия складывается из кинетической и потенциальной энергии и равна максимальной потенциальной или максимальной кинетической энергии:

Круговая частота связана с периодом: . Тогда:

.

Из этого выражения найдем амплитуду:

.

Проверим размерность:

Произведем вычисления:

Ответ: А = 0,32 м, м/с, .

Задача 2. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных гармонических колебаний, данных уравнениями: x₁ = 0,02cos (5t + /2) м и x₂ = 0,03cos (5t + /4) м. Построить векторную диаграмму сложения амплитуд.

Дано: x₁ = 0,02cos (5t + /2)

x₂ = 0,03cos (5t + /4)

Найти: А, . Дать векторную диаграмму.

Решение: Построить векторную диаграмму – это значит представить колебание в виде вектора, длина которого равна амплитуде колебаний, а угол наклона к оси абсцисс равен начальной фазе колебаний. При вращении вектора с угловой скоростью  проекция его конца на ось будет совершать гармонические колебания.

Из условия задачи А₁=0,02 м = 2 см, ₁= 2,

А₂=0,03 м = 3 см, ₂=4.

Векторная диаграмма изображена на рисунке 5.

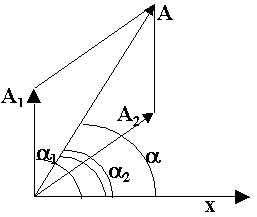
Рис. 5

Результирующую амплитуду найдем по теореме косинусов:

.

Начальная фаза результирующего колебания находится из формулы:

.

Вычисления:

,

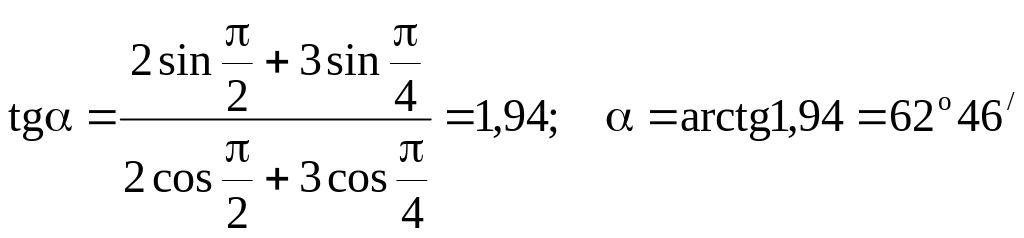
Ответ: А = 4,6 м; =62^о 46^/.

Задача 3. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания =1,6; начальная фаза равна нулю. Смещение точки в начальный момент времени равно 4,5 см. Написать уравнение колебаний и найти смещение точки в момент времени спустя период.

Дано:

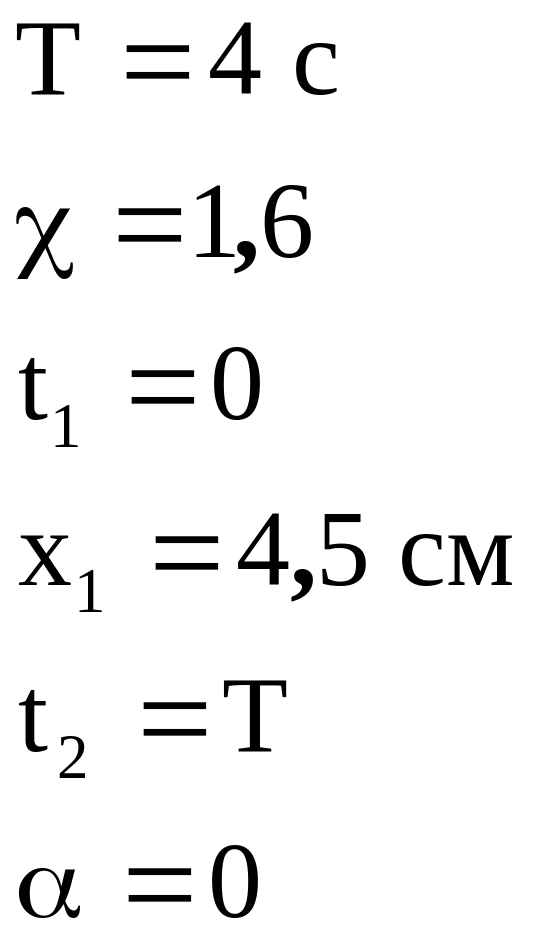
Найти:

Решение: Уравнение затухающих колебаний имеет вид:

, (1)

где  - коэффициент затухания,

 - частота затухающих колебаний.

Найдем :

.

Логарифмический декремент затухания связан с коэффициентом затухания: . Отсюда:

Подставим , ,  в (1) и найдем смещение:

Для начального момента времени при t = 0:

Уравнение колебаний имеет вид:

.

Смещение в момент :

.

Ответ: