4.3 Закон распределения суммы двух случайных величин
При изучении тех или иных явлений приходится сталкиваться со случайными величинами, которые являются результатом суммирования некоторого числа случайных величин. Задача нахождения закона распределения суммы двух и более случайных величин может быть решена следующим образом.
Постановка задачи.
Пусть имеется
система случайных величин (X,Y)
с известной совместной плотностью
распределения f(x,y).
Требуется
определить закон распределения случайной
величины
.
Для решения задачи
обозначим функцию распределения
случайной величины Z,
как
и построим на плоскости x0y
прямую x+
y=z,
которая делит плоскость на две области
(рис.4.1).
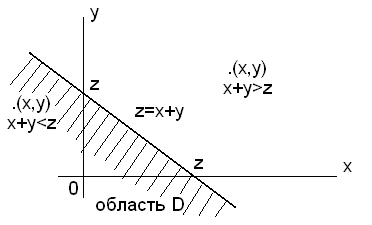
Рисунок 4.1 - График случайной величины
Заштрихованная область на рисунке является областью D.
Вероятность попадания случайной точки z в область D есть функция распределения случайной величины Z, которая по определению равна
.
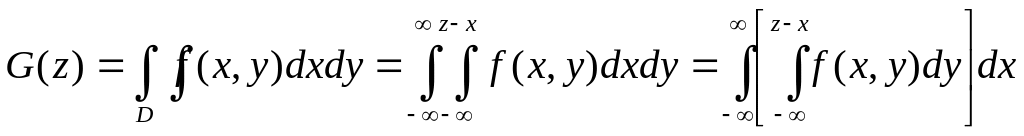Дифференцируя это выражение по переменной z, получим формулу плотности g(z) суммы двух случайных величин X и Y.
.
(4.12)
Аналогично можно получить и формулу плотности g(z), равную
,
(4.13)
которая равносильна формуле (4.12) и может применяться вместо нее.
Если случайные величины X и Y независимы, то закон распределения суммы X+Y называется композицией законов распределения. В этом случае функции в формулах (4.12), (4.13) могут быть представлены в виде:
;
.
Тогда плотность распределения g(z) будет окончательно равна:
;
.
(4.14)
Композиция распределений дискретных случайных величин
Пусть имеется
система ДСВ (X,Y)
с вероятностью совместного распределения
.
Требуется определить закон распределения
случайной величины
,
т.е. найти вероятности
.
(4.15)
Таблица 4.1 иллюстрирует требуемый закон распределения.
Таблица 4.1
zi |
z1 |
z2 |
z3 |
… |
zn |
P(zi) |
P(z1) |
P(z2) |
P(z3) |
… |
P(zn) |
Пример. Дана система дискретных случайных величин (X,Y), закон распределения которой задан таблицей 4.2.
Таблица 4.2
xi\yj |
4 |
3 |
2 |
0,3 |
0,1 |
3 |
0,4 |
0,2 |
Пользуясь выражением (4.14), находим:
;
;
.
На основе полученных вероятностей закон распределения случайной величины можно представить таблицей 4.3.
Таблица 4.3
z |
5 |
6 |
7 |
P(Z) |
0.1 |
0.5 |
0.4 |
Композиция нормальных распределений
Найти плотность
распределения композиции
нормально
распределенных случайных величин X
и Y
с параметрами
,
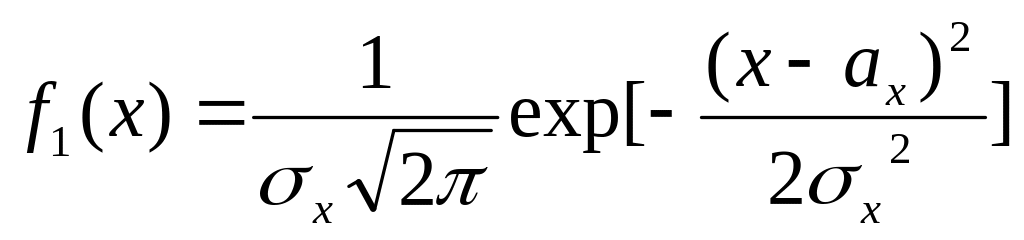если
и
.
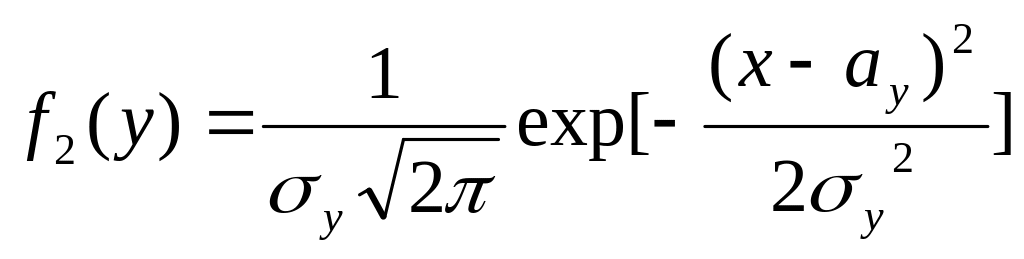Так как по определению плотность распределения композиции равна , то
.
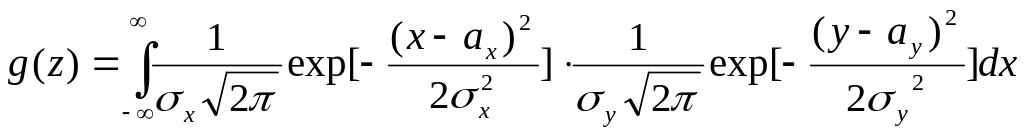Откуда
,
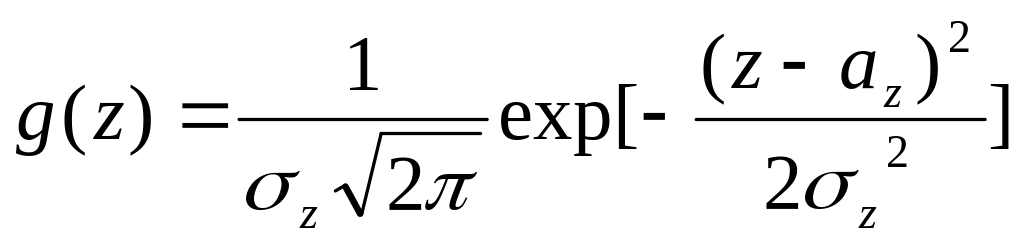где
,
.
(4.16)
Следовательно, в результате композиции двух нормальных распределений суммарный закон получается также нормальным.
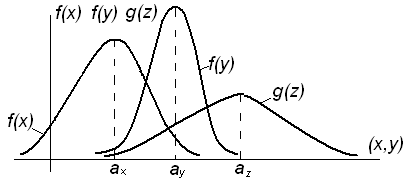
Рисунок 4.2 – Композиция двух нормальных распределений
При композиции произвольного числа нормальных распределений суммарный закон также является нормальным с параметрами:
;
.
Это свойство часто называют устойчивостью нормального закона.
Композиция нормального и равномерного распределений
Пусть случайная величина X подчинена нормальному закону с плотностью распределения
,
а случайная величина Y
распределена равномерно в интервале
[a,
b]:
.
Требуется найти плотность распределения
композиции случайных величин X
и Y.
Решение.
Применяя формулу (4.14), получим
.
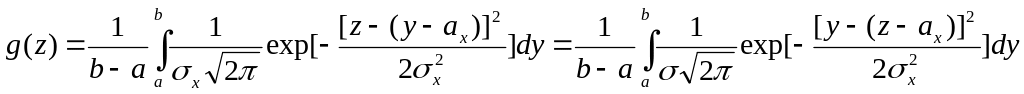Подынтегральная функция есть плотность нормально распределенной случайной величины Y, а интеграл представляет собой вероятность попадания случайной величины в промежуток [a, b].
Следовательно,
.
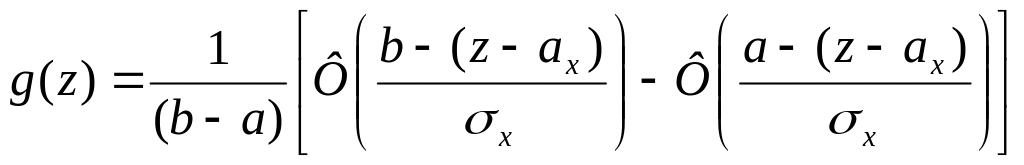(4.17)
Если выполняется неравенство
,
то выражение (4.17) можно отнести к
нормальному распределению:
,
где
,
.
Понятие о центральной предельной теореме Ляпунова
Если случайные
величины
взаимно
независимы и имеют один и тот же закон
распределения с математическим ожиданием
и дисперсией
,
то при неограниченном увеличении n
закон распределения суммы
неограниченно приближается к нормальному
закону:
с параметрами
и
.
Теорема Ляпунова верна и для суммы случайных величин с неодинаковыми законами распределения, у которых дисперсии примерно одного порядка.