2.7 Распределение Пуассона

Распределение Пуассона возникает в случае, когда на появление случайного события влияет много факторов, но каждый фактор в отдельности влияет слабо. Поэтому его и называют законом редких событий.

Случайные величины: поступление вызовов на телефонную станцию; число отказов элементов при испытании на надежность сложного электронного устройства; число бракованных изделий в выборках из партий, изготавливаемых заводом изделий и т. д. имеют пуассоновское распределение.

Это распределение можно рассматривать как предельный случай биномиального распределения, когда число случаев , а вероятность события в отдельном опыте стремится к нулю . Тогда МО числа событий определится как произведение . Откуда вероятность события в одном опыте будет равна , а вероятность m событий в n опытах можно найти по формуле Бернулли

Так как число случаев , то

, и .

Следовательно, выражение для распределения Пуассона (индекс n не пишут, поскольку n велико) будет иметь вид

,

где ; p - можно трактовать как МО числа появлений события в одном опыте.

В ряде практических задач величина a может определяться как:

;

;

;

,

где l, s, v, t – длина, площадь, объем и время соответственно;

- математическое ожидание числа появлений события или на участке единичной длины, или на единичной площади, или в единичном объеме, или в единичном интервале времени.

Определим математическое ожидание и дисперсию случайной величины, имеющей пуассоновское распределение. Из определения МО случайной дискретной величины следует

, где ; .

После подстановки получаем

. Поэтому M[X]=a.

Для нахождения дисперсии воспользуемся формулой

. Откуда D[X]=a.

Таким образом, математическое ожидание равно дисперсии, если случайная величина имеет пуассоновское распределение.

Вероятность попадания случайной величины на заданный участок, распределенной по закону Пуассона, определяется по выражению

.

2.8 Экспоненциальное распределение

В различных приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике и т.д. широко применяется экспоненциальное (показательное) распределение.

Время занятости канала связи, время безотказной работы ЭВМ, продолжительность поиска чего–либо – все это экспоненциально распределенные случайные величины.

Неотрицательная величина X называется распределенной по экспоненциальному закону, если ее плотность распределения имеет вид

,

где - параметр экспоненциального распределения.

График плотности распределения изображен на рис. 13.

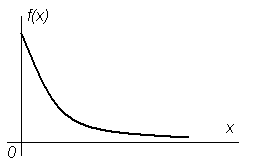
Рисунок 13 График плотности вероятности экспоненциально распределенной случайной величины

Определим основные числовые характеристики этого распределения:

,

т.е. математическое ожидание есть величина обратная параметру закона. Для отыскания дисперсии используем формулу

. Откуда средне – квадратичное отклонение будет равно

.

Вероятность попадания случайной величины на заданный участок, распределенной экспоненциально можно рассчитать, используя формулу

.

Вопросы для повторения

1 Какая величина называется случайной? Приведите примеры.

2 В чем отличие непрерывной случайной величины от дискретной?

3 Что понимают под законом распределения случайной величины?

4 На какие вопросы позволяет ответить ряд распределения и многоугольник распределения случайной величины?

5 Что называется функцией распределения? Как, зная функцию распределения случайной величины, определить вероятность попадания случайной величины в заданный интервал?

6 Что называется плотностью вероятности? Что она характеризует?

7 Как, зная плотность вероятности случайной величины, определить вероятность попадания случайной величины в заданный интервал?

8 Какими свойствами обладает математическое ожидание случайной величины и что физически оно характеризует?

9 Какими свойствами обладает дисперсия случайной величины и что физически она характеризует?

10 Какое применение находит среднее квадратичное отклонение?

11 Изобразите графики интегральной и дифференциальной функции распределения случайной величины, имеющей:

равномерное распределение;

нормальное распределение;

экспоненциальное распределение.

12 Как определяются числовые характеристики и вероятность попадания случайной величины в заданный интервал в случае ее:

равномерного распределения;

нормальное распределение;

экспоненциальное распределение.

13 В чем заключается сущность пуассоновского распределения? Чему равны числовые характеристики случайной величины с этим распределением?

Упражнения

2.1 Вычислите функцию распределения F(x) при x=3, если дискретная случайная величина описана рядом:

x: 0 2 3 5

p: 0.1 0.6 0.1 0.2.

2.2 Определите вероятность попадания дискретной случайной величины в интервал =2, =4, если известен ее ряд распределения:

x 0 1 2 3 4 5

p 0.1 0.2 0.1 0.3 0,05 0,25.

2.3 Аппаратура состоит из 50 узлов. Вероятность отказа каждого узла в течение 100 часов работы одинакова и равна 0,1. Найти математическое ожидание числа отказавших узлов за 100 часов работы.

2.4 Найдите МО дискретной случайной величины х, заданной рядом распределения:

х: -2 5 10

р: 0,2 0,3 0,5.

2.5 Найдите дисперсию дискретной случайной величины X – числа отказов элементов некоторого устройства в 20 независимых опытах, если вероятность отказа элемента в каждом опыте равно 0,3.

2.6 Дискретная случайная величина задана рядом распределения

х: 2 4 7

р: 0,5 0,2 0,3.

Найдите дисперсию случайной величины.

2.6 Непрерывная случайная величина распределена равномерно в интервале (3;9). Найдите математическое ожидание случайной величины.

2.7 Непрерывная случайная величина распределена равномерно в интервале (2;8). Найдите дисперсию случайной величины.

2.8 Непрерывная случайная величина распределена равномерно в интервале (0;10). Найдите вероятность попадания случайной величины в заданный интервал (3;5).

2.9 Требуется найти вероятность попадания нормально распределенной случайной величины в интервал (5;9), если a =5, .

2.10 Вычислите дисперсию случайной величины T, если плотность распределения ее равна .

2.11 Случайная величина X распределена нормально с математическим ожиданием a=10. Вероятность попадания X в интервал (10;20) равна 0.3. Чему равна вероятность попадания X в интервал (0;10)?

2.12 Случайная величина X распределена нормально со средне квадратичным отклонением . Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0.9973 попадет случайная величина X в результате испытания.

2.13 Найдите дисперсию показательного распределения, заданного плотностью вероятности .

2.14 Найдите средне квадратичное отклонение случайной величины от центра группирования показательного распределения, заданного функцией распределения .