Релятивистская динамика

Релятивистский импульс

В классической механике    ,  при v << c.

В релятивистской механике, где v → c,

.

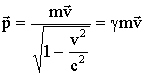Выражение для релятивистского импульса отличается от классического множителем γ.

Уравнение движения в релятивистской механике такое же, как и в классической

      но      

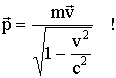
Релятивистское выражение для энергии

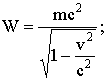
Энергия покоя

При скорости материальной точки v=0

Кинетическая энергия (энергия движения)

.

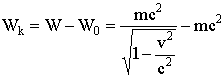Или , m – масса покоя

Релятивистские инварианты

Масса покоя m

Скорость света С

Время жизни в собственной системе отсчета

Интервал

Энергетический инвариант

Из этого следует, что

- inv, инвариант,

т.е. не зависит от выбора системы отсчета.

Интервал

Интервал между событиями 1 и 2

Доказательство

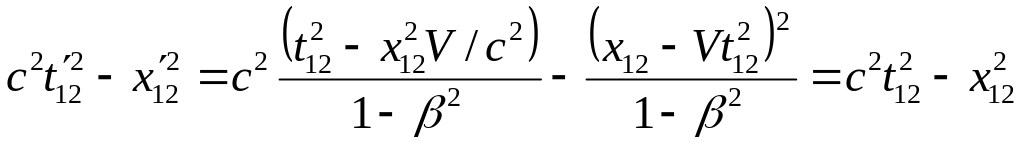
Как видим, слева и справа стоят одинаковые по форме выражения.

Типы интервалов

1. Пространственноподобный

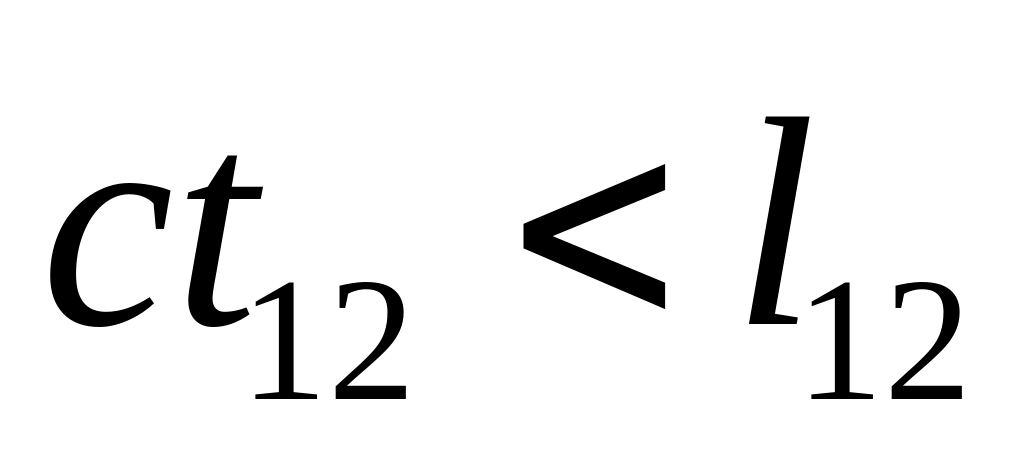
события не могут быть связаны причинноследственной связью

2. Времениподобный

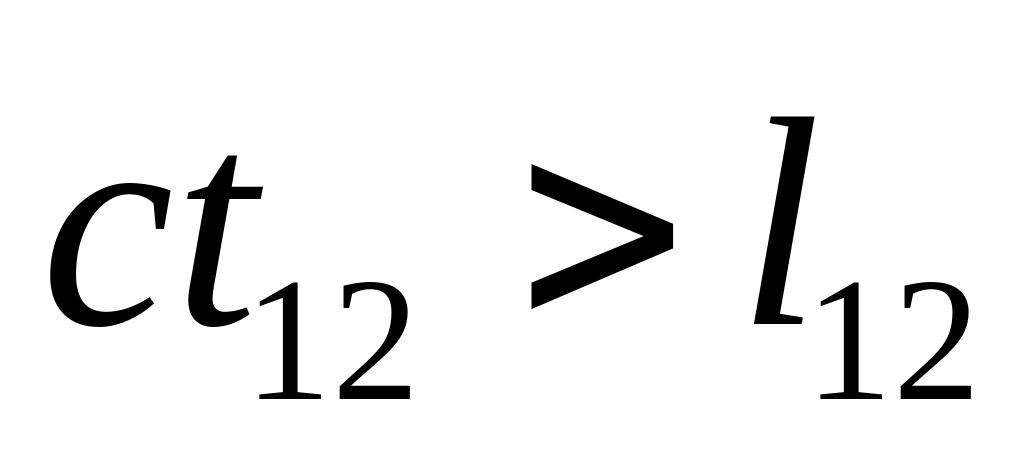
события могут быть связаны причинноследственной связью

3. Светоподобный

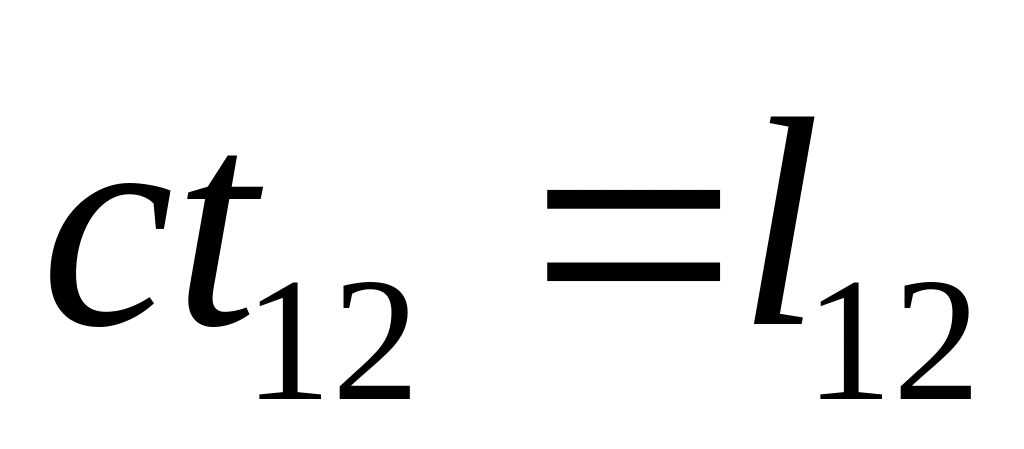
ict

Абсолютное будущее

∙2

x

Здесь и сейчас событие1

Абсолютное прошлое

Динамика сто

1. Релятивистский импульс и закон сохранения импульса

Ньютоновский импульс не сохраняется

Релятивистский импульс сохраняется

2. Релятивистская масса

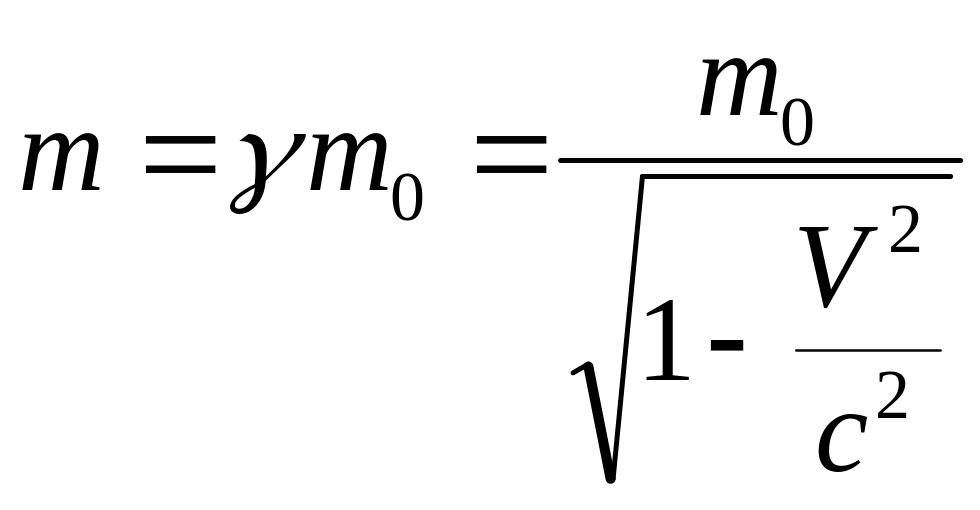
3. Основное уравнение релятивистской динамики

4. Сила и ускорение

5. Кинетическая энергия частицы

По теореме о кинетической энергии запишем

Выражение для силы возьмём из уравнения динамики

поэтому кинетическая энергия

Теперь распишем релятивистскую массу и возьмём дифференциал этого уравнения

Комбинируя это с выражением для энергии, получим , что малое изменение энергии пропорционально изменению массы.

Интегрируя, получаем, что кинетическая энергия равна разности полной энергии и энергии покоя или , что по виду сильно отличается от классического выражения. Однако если разложить в ряд

получим при обычное классическое выражение . Работа, затрачиваемая на ускорение частицы (приобретение Т) по прежнему равна

.

6. Взаимосвязь массы и полной энергии

Определим полную энергию как сумму энергии покоя и кинетическую энергию

Тем самым Эйнштейн положил, что любое тело массой обладает энергией покоя , а полная его энергия , как видно в неё не включается потенциальная энергия тела во внешнем поле, даже если таковое и действует на тело.

7. Связь полной энергии и импульса частицы

По отдельности энергия и импульс не являются инвариантными, но есть их комбинация, которая будет inv. Энергия покоя инвариант

Следовательно

8. Частицы с нулевой массой покоя

Рассмотрим новые определения полной энергии и импульса

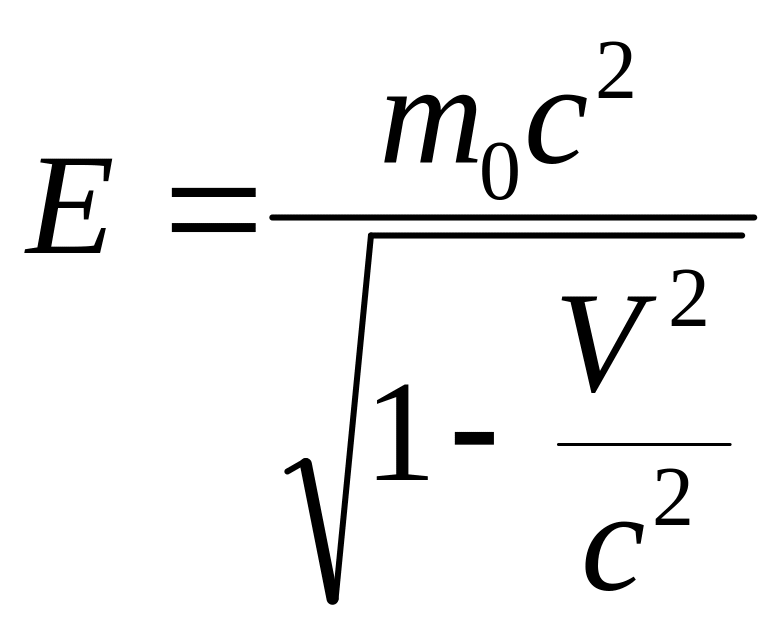и

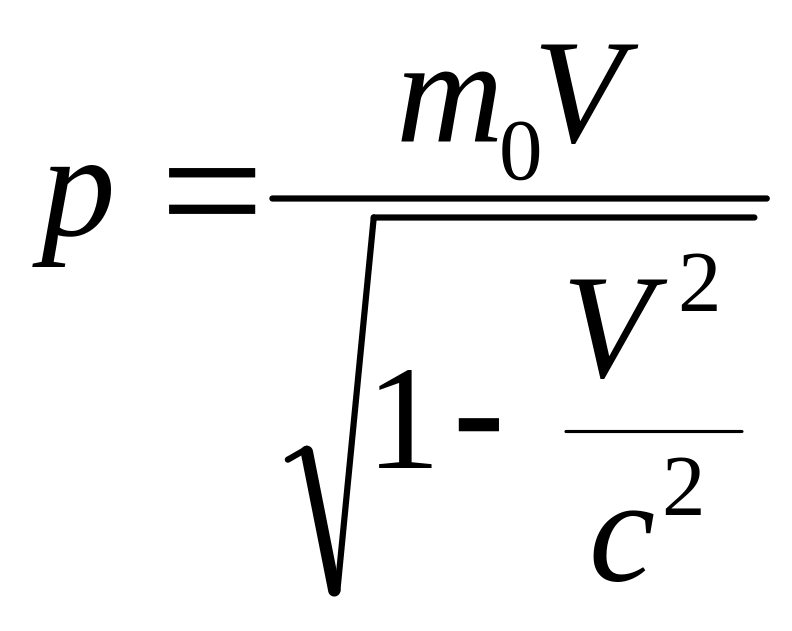
Из них следует, что могут существовать частицы с и

Такие есть в природе – это фотоны (и нейтрино-?). Связь энергии и импульса для них простая

Закон сохранения релятивистского импульса

41