5. Динамика вращательного движения

Работа при вращательном движении. Момент силы

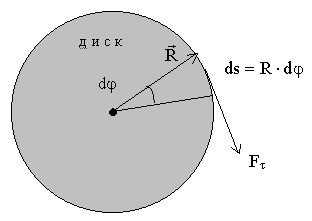
Элементарная работа на пути ds=Rd равна , где момент силы относительно оси вращения z (вращающий момент)

.

В векторном виде:

- векторное произведение.

Кинетическая энергия при вращательном движении. Момент инерции

.

.

I_z - момент инерции твердого тела, относительно оси z.

Моментом инерции материальной точки I_i называется величина:

.

Для N материальных точек

Для сплошного тела и для вычисления момента инерции твердого тела необходимо брать интегрирал (учтено, что dm=dv).

Величина I зависит от положения оси вращения и от распределения масс в теле.

Теорема Штейнера

,

где I₀ - момент инерции относительно оси OО, I - момент инерции относительно оси O'О'.

Моменты инерции I₀ для некоторых тел (относительно оси, проходящей через центр масс).

Для сплошного тела момент инерции

1. Обруч массой m и радиусом R с однородным распределением массы:

 dv = dm

2. Полый цилиндр – состоит из одинаковых обручей:

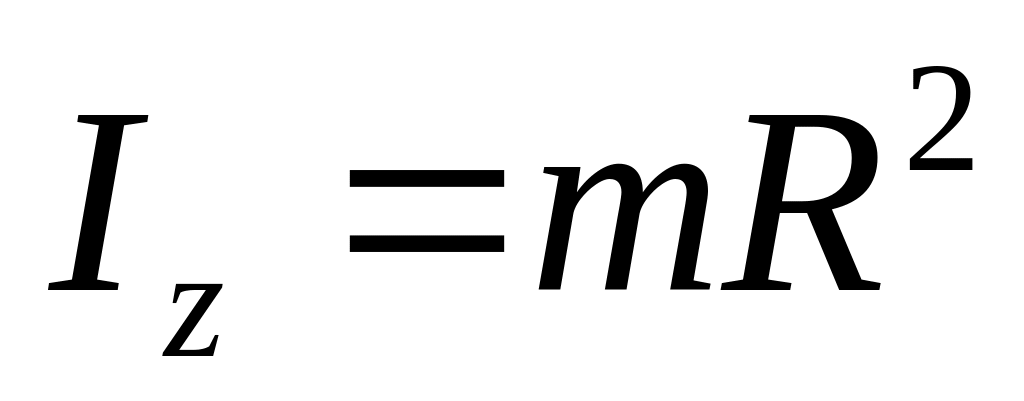
3. Сплошной цилиндр. Выделим элемент площади ds = 2 r ,

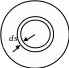элемент объёма dv = hds=2 rh.

4. Тонкий однородный стержень длиной L.

1. Ось проходит через середину стержня.

э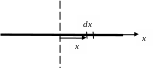 лемент массы dm = dx ( – линейная плотность массы).

2. Ось проходит через конец стержня.

По теореме Штейнера

5. Ш 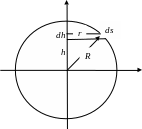ар. Разобьем шар на плоские цилиндры (блины) шириной dh: объём,

радиус и масса этого элементарного цилиндра

dv =  r²dh , r² = R² - h² , .

Момент инерции этого элементарного цилиндра .

Интегрируя по h от 0 до R и удваивая, получим

6. Шаровой слой. Внутренний и наружный радиусы: R₁ и R₂.

7. Сферическая оболочка.

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции Ja
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра
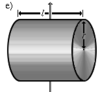
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
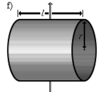
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
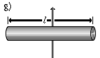
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
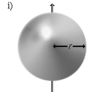
	Шар радиуса r и массы m	Ось проходит через центр шара
	Конус радиуса r и массы m	Ось конуса
	Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершну
	Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс
	Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс

Уравнение динамики вращательного движения (упрощённый вывод) Работа и кинетическая энергия .

Для вращательного движения .

или ,

Откуда .

Получим основное уравнение динамики вращательного движения

или в векторном виде .

Как и линейное ускорение ( ) вектор углового ускорения определяется вектором момента силы.

Момент импульса абсолютно твердого тела Момент силы

,      или       .

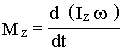Введем момент импульса абсолютно твердого тела:

.

В векторном виде для однородного симметричного тела:

. Как и импульс ( ) момент импульса сонаправлен с угловой скоростью

Закон изменения момента импульса со временем:

                ,

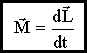Закон сохранения момента импульса ,

если момент силы = 0, то: .

Т.к. , то величина будет иметь одинаковые значения для любых интересующих нас моментов времени, т. е.:

;

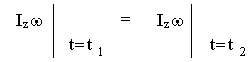
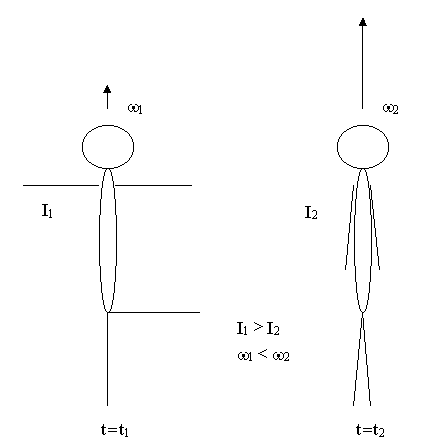или .

Вращающееся тело может изменить свой момент инерции, изменится и его угловая скорость, но при равенстве нулю суммарного момента внешних сил величина I_zω останется постоянной. Пример - фигурист в "волчке".