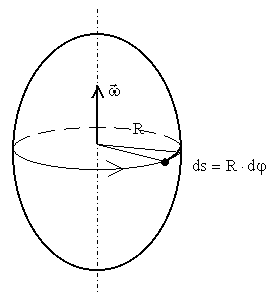
- •1. Кинематика
- •1. Основные понятия
- •2. Динамика материальной точки
- •3.Законы сохранения
- •4. Кинематика вращательного движения
- •5. Динамика вращательного движения
- •Осевые моменты инерции некоторых тел
- •Момент силы Момент импульса Момент инерции в ектор Вектор скаляр
- •Принцип постоянства скорости света:
- •Релятивистская динамика
- •Интервал
- •Динамика сто
4. Кинематика вращательного движения
Поступательное и вращательное движение
|
В данном примере траектория центра масс - окружность, остальные точки тела также движутся по окружностям , но центры этих окружностей не лежат на одной прямой. |
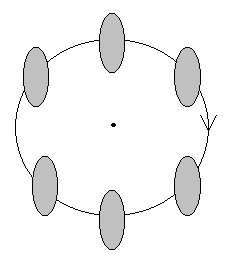
а) поступательное движение. Любая линия, проведенная в твердом теле, при движении остается параллельной самой себе.
|
Здесь, как и в предыдущем примере а), центр масс тела движется по той же окружности. |
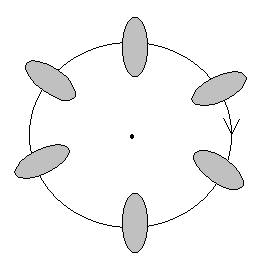
б) вращательное движение, центр масс движется по окружности того же радиуса. Каждая точка твердого тела движется по своей окружности; центры всех окружностей лежат на прямой, называемой осью вращения.
Псевдовектор бесконечно малого поворота
|
При повороте
тела на угол dφ, вводят псевдовектор
бесконечно малого поворота
|
Угловая скорость
|
Угловое
ускорение
|
Связь линейной скорости материальной точки твердого тела и угловой скорости
|
откуда
получаем важную связь линейной и
угловой скоростей
где радиус вектор
|
Связь линейного ускорения материальной точки твердого тела с угловой скоростью и угловым ускорением
Продифференцируем по времени:
![]() ,
,
![]() ,
,
![]() следовательно,
следовательно,
![]() или
векторно
или
векторно
![]() .
.
![]() , заменяя V
на
, заменяя V
на
![]() ,
получим
,
получим
![]() .
.
Полное
ускорение
![]() .
.
Зачем нужна векторная запись этих соотношений (?!!!)
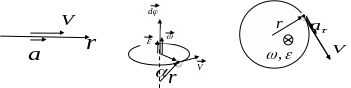
Пример ускоренного движения м. точки в положительном направлении (вперёд).
М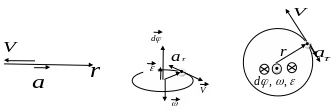 одуль
векторного произведения
одуль
векторного произведения
![]()
Пример замедленного движения м. точки в отрицательном направлении (назад).
Векторное произведение – правая тройка векторов (правый винт) – вычисление через определитель:
Векторы
имеют проекции:
![]() ;
;
![]() ,
тогда
в общем виде
,
тогда
в общем виде
![]() .
.
Проекции
вектора
![]()
![]() ;
;
![]() ;
;
![]() .
.
При
наличии только одной проекции угловой
скорости
![]() и
двух проекций радиуса вектора
и
двух проекций радиуса вектора
![]() получим для линейной скорости только
y-ю
проекцию
получим для линейной скорости только
y-ю
проекцию
![]() .
.
Кинематический закон вращательного движения.
Из определения углового ускорения
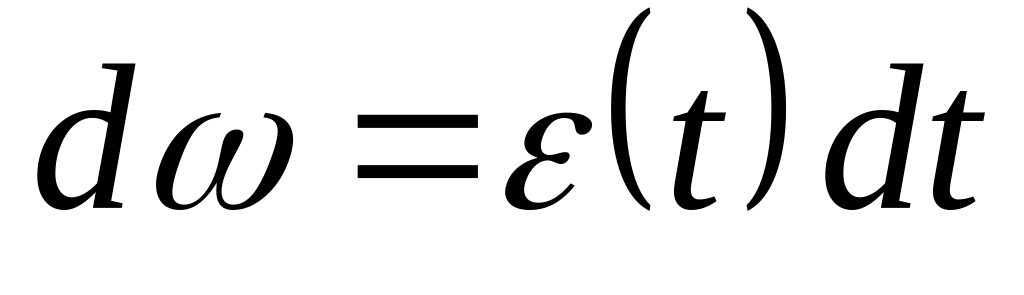 находится
угловая скорость как функция времени:
находится
угловая скорость как функция времени:
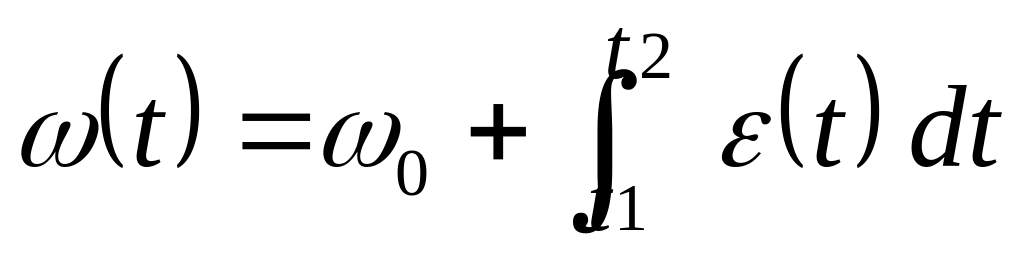 .
(0
– константа интегрирования).
.
(0
– константа интегрирования).Из определения угловой скорости
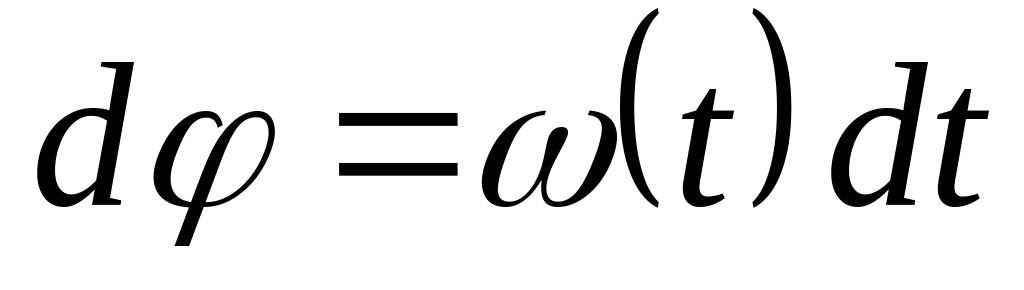 находится
угол как функция времени:
находится
угол как функция времени:
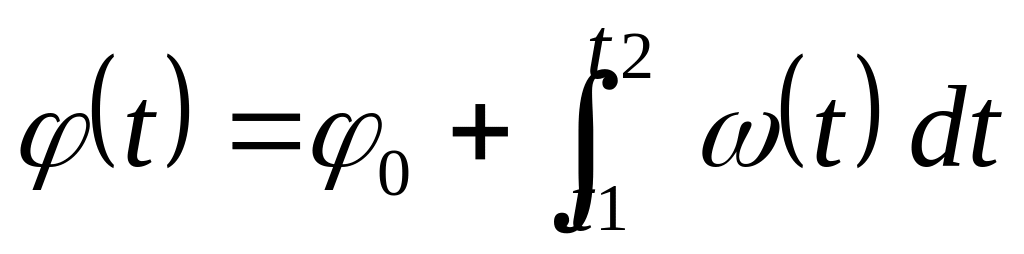 .
(0
– константа интегрирования).
.
(0
– константа интегрирования).
Для
частного случая
![]() ,
получаем закон равнопеременного движения
по окружности:
,
получаем закон равнопеременного движения
по окружности:
![]() –
квадратичная зависимость угла поворота
от времени
–
квадратичная зависимость угла поворота
от времени
и линейная зависимость угловой скорости
от времени
![]() .
.
При этом одинаковым знакам для угловых
скорости и ускорения
![]() соответствует
ускоренное движение, а разным знакам
соответствует
ускоренное движение, а разным знакам
![]() – замедленное.
– замедленное.



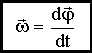 ,
или
,
или