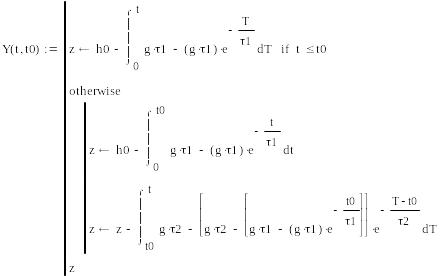- •1. Кинематика
- •1. Основные понятия
- •2. Динамика материальной точки
- •3.Законы сохранения
- •4. Кинематика вращательного движения
- •5. Динамика вращательного движения
- •Осевые моменты инерции некоторых тел
- •Момент силы Момент импульса Момент инерции в ектор Вектор скаляр
- •Принцип постоянства скорости света:
- •Релятивистская динамика
- •Интервал
- •Динамика сто
2. Динамика материальной точки
Инерциальные системы отсчета. Первый закон Ньютона
Инерциальная система отсчета - это система отсчета, в которой тела, не подверженные воздействию других тел, движутся прямолинейно и равномерно. Первый закон Ньютона:
Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
С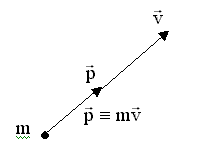 ила
ила![]() - векторная величина, характеризующая
воздействие на данное тело других тел.
Величину силы можно определить опытным
путем, используя прибор для измерения
силы - динамометр.
- векторная величина, характеризующая
воздействие на данное тело других тел.
Величину силы можно определить опытным
путем, используя прибор для измерения
силы - динамометр.
Масса тела, m, - скалярная величина, являющаяся мерой инертности тела. Импульс материальной точки - это вектор, равный, в механике Ньютона, произведению массы точки на ее скорость.
Второй закон Ньютона Скорость изменения импульса равна действующей на материальную точку результирующей силе: .
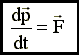 ,
где
,
где
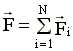
![]()
п![]() ри
m ≠ m(t)
ри
m ≠ m(t)
т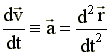 .к
.к
то ![]()
![]()
Третий закон Ньютона
Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению. Пример - взаимодействие двух электрических зарядов:
![]()
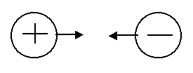
Из третьего закона Ньютона следует, что для каждой силы можно указать тело, являющееся причиной этой силы. Если же указать такое тело - причину возникшей силы - не удается, то тогда причина "силы" - неинерциальность системы отсчета. Напомним, что законы Ньютона справедливы только в инерциальных системах отсчета.
Уравнения движения.
Второй
закон механики (з. Ньютона) позволяет
записать уравнение
движения
тела (м.т.): это уравнение вида
![]() ,
из
которого путем двойного интегрирования
находится закон движения
,
из
которого путем двойного интегрирования
находится закон движения
![]() при
задании шести начальных условий. Это
уравнение эквивалентно трем скалярным
неоднородным дифференциальным уравнениям
второго порядка (в общем случае трёхмерного
движения).
при
задании шести начальных условий. Это
уравнение эквивалентно трем скалярным
неоднородным дифференциальным уравнениям
второго порядка (в общем случае трёхмерного
движения).
Для системы N тел необходимо интегрировать 3N уравнений с 6N начальными условиями. Сложность этих уравнений определяется видом сил. В общем случае силы могут зависеть от координат всех тел, их скоростей и времени (всего 6N +1 переменных). Аналитически эта задача разрешима только для системы двух тел, взаимодействующих гравитационно – задача Кеплера. Уже для трех тел (Солнце, Земля, Луна) эта задача в квадратурах не разрешима.
Пример
интегрирования уравнений движения в
одномерном случае: прыжок парашютиста.
Человек массы m
прыгает с высоты h0,
а через t
секунд раскрывает парашют – пример
тела, двигающегося в вязкой среде с
коэффициентом аэродинамического
сопротивления r.
Кроме постоянной силы тяжести на него
действует аэродинамическая сила
сопротивления воздуха, пропорциональная
скорости
![]() .
.
Уравнение
движения
запишем в виде
![]() .
Перепишем
в виде, удобном для интегрирования и
проинтегрируем,
.
Перепишем
в виде, удобном для интегрирования и
проинтегрируем,
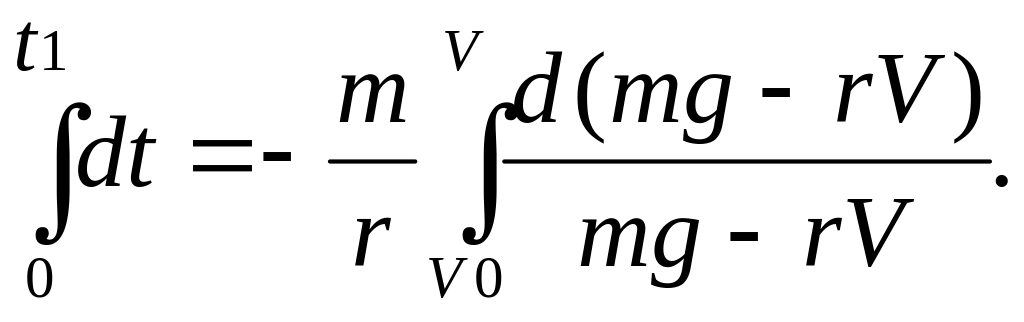 В результате найдём зависимость времени
от скорости
В результате найдём зависимость времени
от скорости
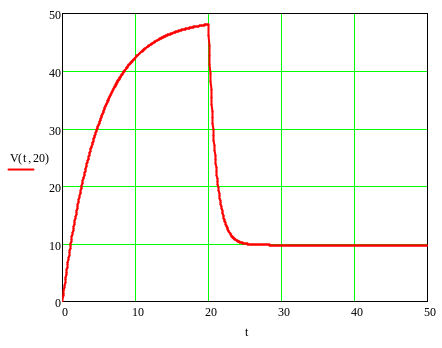
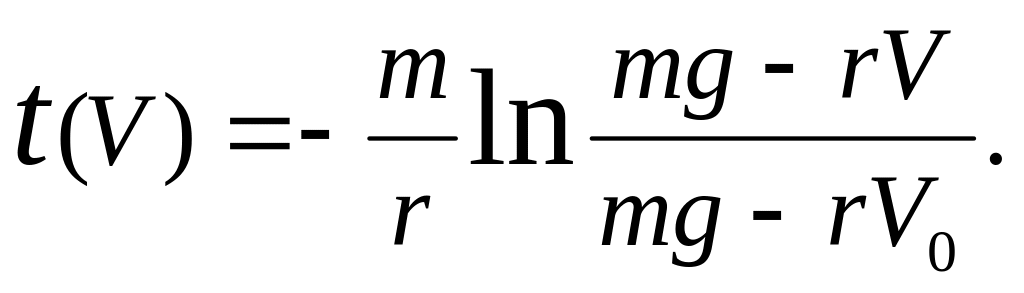 Обратная
зависимость скорости от времени
Обратная
зависимость скорости от времени
![]() ,
где
,
где
![]() –
характерное
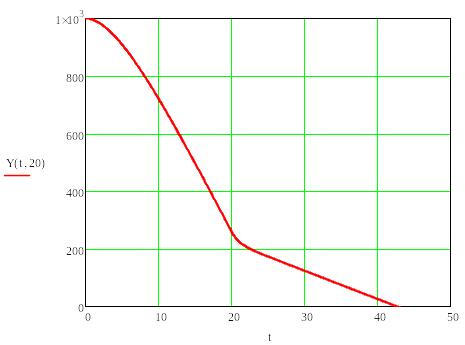
время. Зависимость y-вой
координаты от времени
–
характерное
время. Зависимость y-вой
координаты от времени
![]() .
.
Начальная высота h0 = 1000 м, начальная скорость V0 = 0.