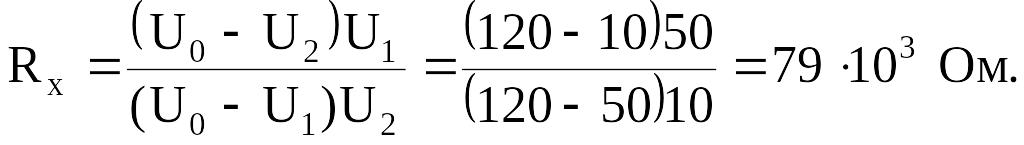Решение. В основном уравнении молекулярно- кинетической теории –

.

Произведение nm выражает массу молекул, содержащихся в единице объема вещества, и следовательно, равно плотности ρ газа. Таким образом,

Па.

Пример 18. 6,5 г водорода, температура которого 27⁰ С, расширяется вдвое при постоянном давлении за счет притока тепла извне. Найти: а) изменение внутренней энергии; б) количество теплоты, сообщенной газу; в) работу расширения. (М_в=210^-3 кг/моль).

Решение. Вычислим значения молярных теплоемкостей водорода, учитывая, что молекулы водорода – двухатомные, а число I степеней свободы равно пяти:

=20,8·10³ Дж/мольК;

C_р =C_v + R=20,8·10³ + 8,31·10³ =29,1·10³ Дж/мольК.

Используя условие задачи и уравнение для изобарического процесса

,

найдем температуру газа после расширения:

Т₂ = =2Т₁ = 600 К.

Вычислим изменение внутренней энергии и количество тепла:

=20,3·10³ Дж;

=28,4·10³ Дж.

На основании первого начала термодинамики найдем работу расширения газа:

А=Q–∆U=28,4·10³–20,3·10³ Дж=8,1·10³ Дж.

Пример 19. Воздух, занимавший объем V₁=10 л при давлении Р₁=100 кПа, был адиабатически сжат до объема V₂ =1 л. Под каким давлением Р₂ находится воздух после сжатия?

Решение. Поскольку совершается адиабатический процесс, для решения используем уравнение адиабаты в виде

.

Отсюда следует, что

_.

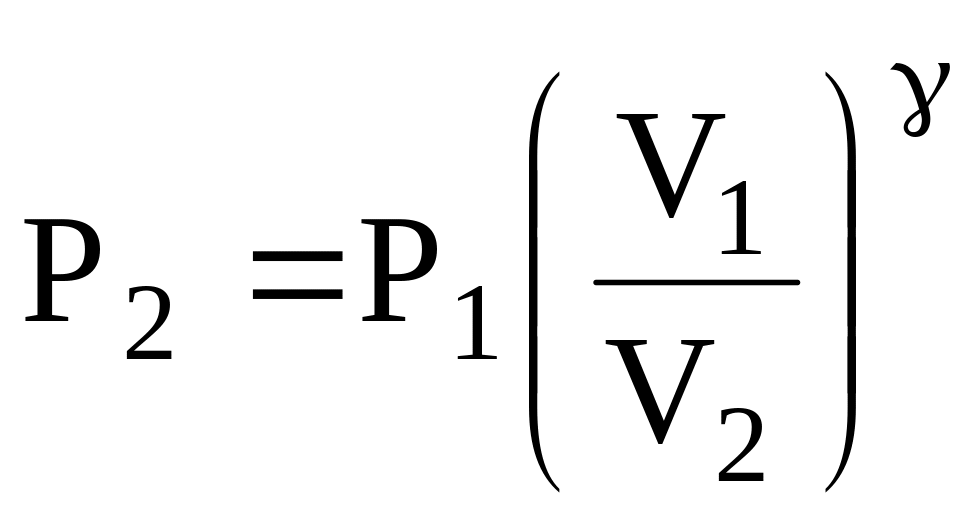Показатель Пуассона –

,

где i=5, так как считаем воздух состоящим в основном из двухатомных молекул. Подставив в формулу для P₂ численные значения величин, получим:

P₂ = =10⁵ ·10^1,4 =10^6,4 Па.

В итоге логарифмирования имеем gР₂ = 6,4. На основании этого Р₂=2,51·10⁶ Па.

Пример 20. Тепловая машина работает по обратному циклу Карно. Температура теплоотдатчика Т₁=500 К. Определить термический кпд цикла и температуру Т₂ теплоприемника тепловой машины, если за счет каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу А=350Дж.

Решение. Термический кпд тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу:

,

где А – работа, совершаемая рабочим телом; Q₁ – теплота, полученная от теплоотдатчика.

По формуле

η= ,

зная η цикла, можно определить температуру охладителя Т₂ :

.

Произведем вычисления:

, .

Пример 21. В вершинах равностороннего треугольника находятся одинаковые положительные заряды Q₁=Q₂=Q₃=1 нКл (см. рисунок). Какой отрицательный Q₄ необходимо поместить в центр треугольника, чтобы сила притяжения с его стороны уравновесила силы отталкивания зарядов, находящихся в вершинах?

Решение. Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Заряд Q будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю:

,

где – равнодействующая сил и ; .

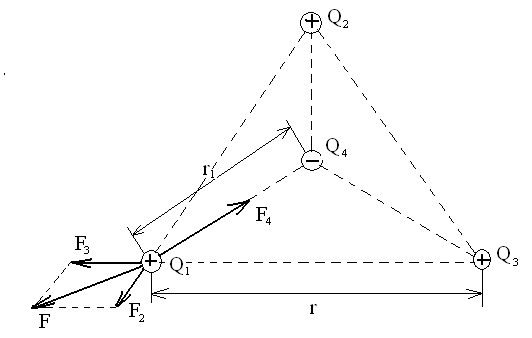
Выразив F через F₂ и F₃ (с учетом того, что = ), получим

.

По закону Кулона

,

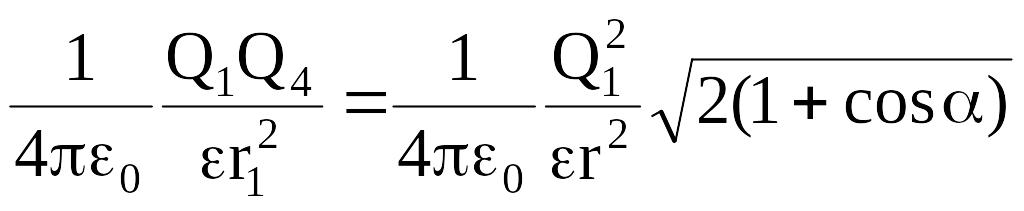откуда

.

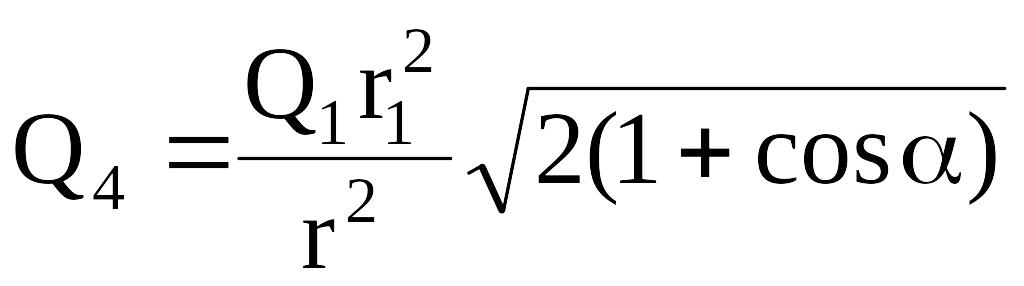Выразим 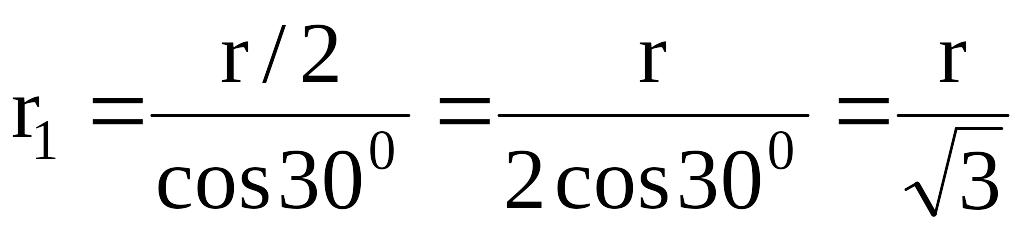; cosα=cos60⁰=1/2.

C учетом этого мы получим

.

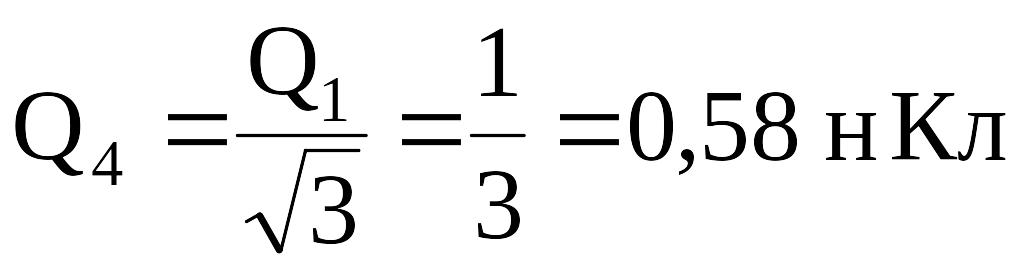Пример 22. Кольцо радиусом r=5 см из тонкой проволоки равномерно заряжено с линейной плотностью =14 нКл/м (см. рисунок). Определить напряженность поля на оси, проходящей через центр кольца, в точке, удаленной на расстоянии а=10 см от центра кольца.

Решение. Элемент кольца d имеет заряд dQ=τd .

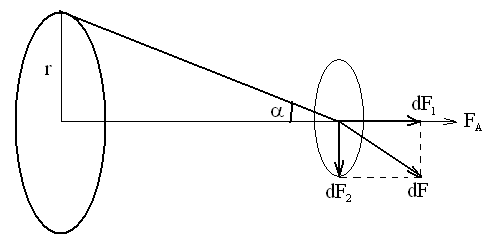
Напряженность электрического поля в точке А, создаваемая этим элементом, 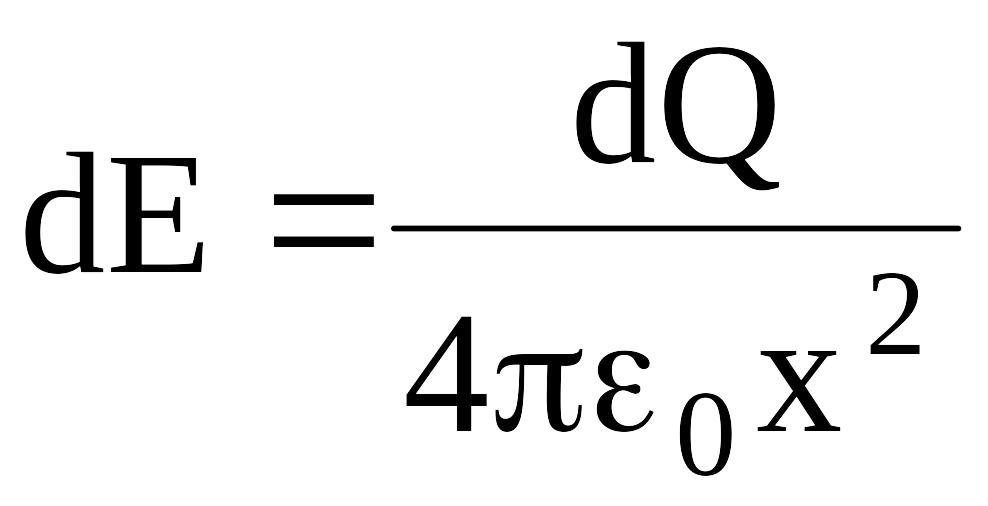. Она направлена по линии, соединяющей элемент кольца d с точкой А. Для нахождения напряженности поля всего кольца надо векторно сложить от всех элементов. Вектор можно разложить на составляющие и . Составляющие каждых двух диаметрально противоположных элементов взаимно уничтожаются, и тогда , а ;

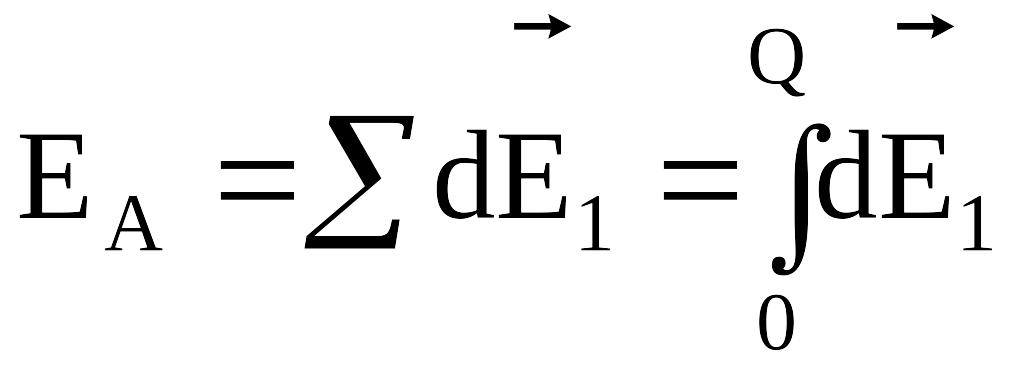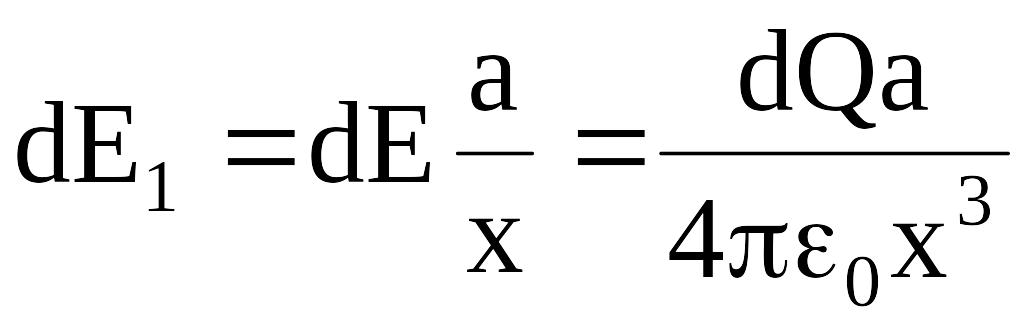, но ,

,

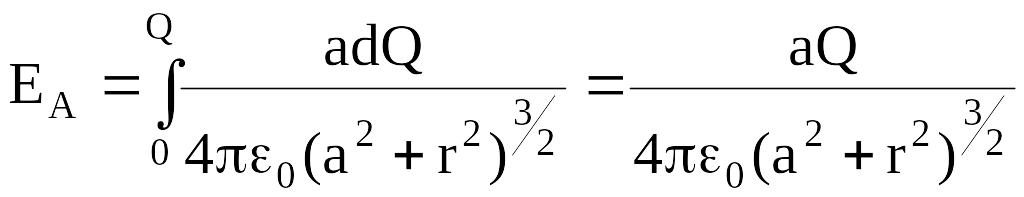где Q − заряд кольца, . Тогда

.

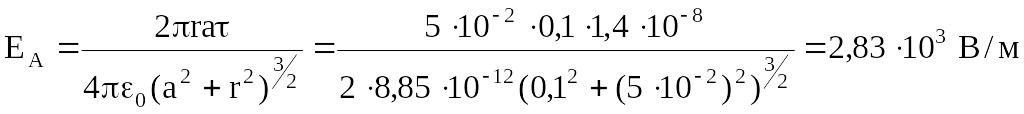Пример 23. Конденсатор емкостью С₁=3 мкФ был заряжен до разности потенциалов U₁=40 В. После отключения от источника тока конденсатор соединили параллельно с другим незаряженным конденсатором емкостью С₂=5 мкФ. Какая энергия W израсходуется на образование искры в момент присоединения второго конденсатора?

Решение: Энергия, израсходованная на образование искры, −

, (1)

где – энергия, которой обладал первый конденсатор до присоединения к нему второго конденсатора; – энергия, которую имеет батарея, составленная из двух конденсаторов.

Энергия заряженного конденсатора определяется по формуле

, (2)

где С – емкость конденсатора или батареи конденсаторов.

Выразив в формуле (1) энергии и по формуле (2) и приняв во внимание, что общая емкость параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов, получим

, (3)

где U₂ – разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора остался прежним, выразим разность потенциалов U₂ следующим образом:

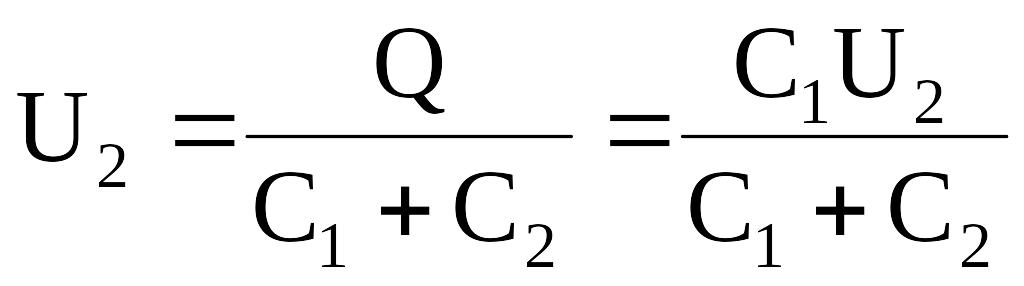. (4)

Подставив выражение U₂ в (3), найдем

,

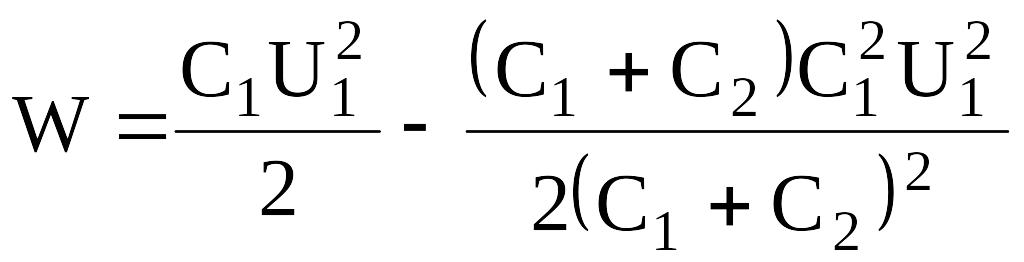или

.

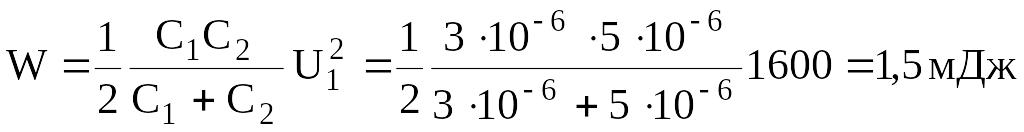Пример 24. Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение t=2 с по линейному закону от I₀=0 до I=6 А. Определить теплоту, выделившуюся в этом проводнике за первую секунду(Q₁), за вторую секунду (Q₂), а также найти отношение .

Решение. Закон Джоуля-Ленца в виде справедлив для постоянного тока (I=const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала и записывается в виде

. (1)

В данном случае сила тока является некоторой функцией времени

, (2)

где – коэффициент пропорциональности, характеризующий скорость изменения силы тока:

.

С учетом (2) формула (1) примет вид

. (3)

Для определения теплоты, выделившейся за конечный интервал времени t, выражение (3) надо проинтегрировать в пределах от t₁ до t₂:

.

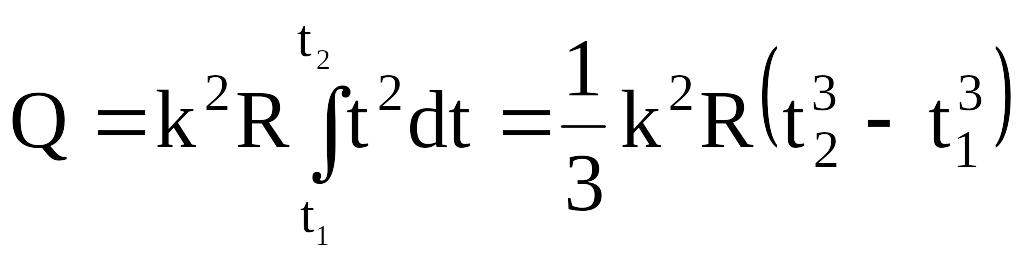Произведем вычисления:

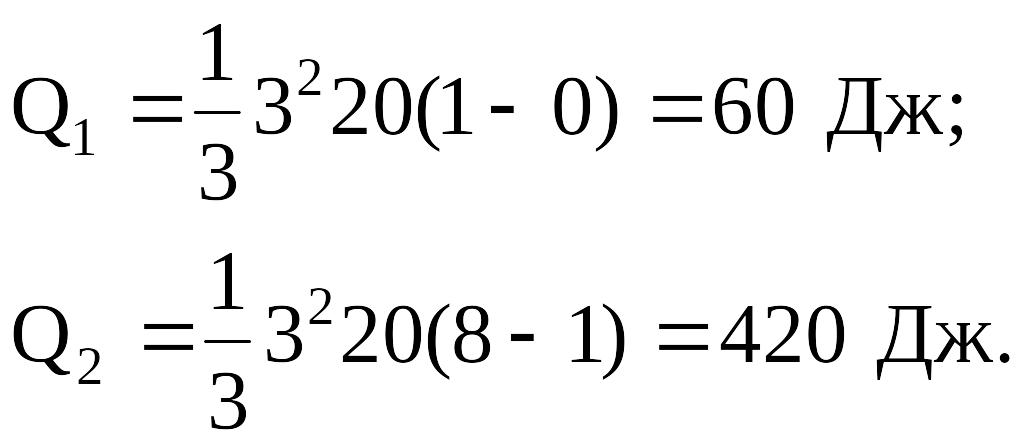
Следовательно, .

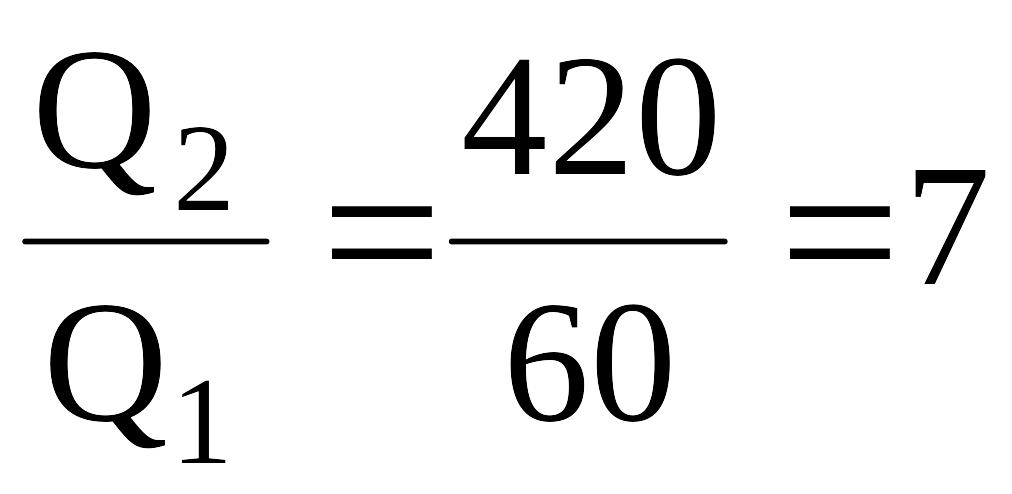Пример 25. Если вольтметр соединить последовательно с сопротивлением R=10 кОм, то при напряжении U₀=120 В он покажет U₁=50 В. Если соединить его последовательно с неизвестным сопротивлением R_х, то при том же напряжении вольтметр покажет U₂=10 В. Определить это сопротивление.

Решение. Данная цепь представляет собой последовательное соединение двух элементов: вольтметра и сопротивления. При последовательном соединении сила тока одинакова на всех участках цепи. Рассматриваемая цепь является однородной:

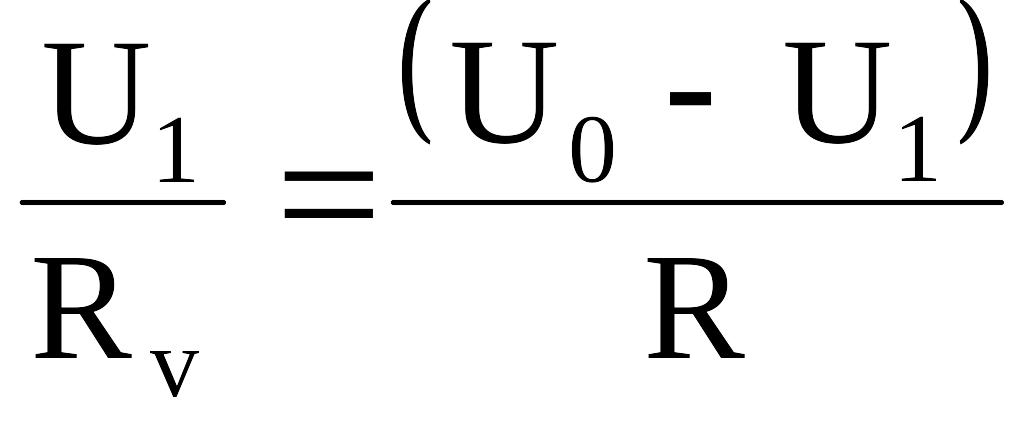, (1)

где U₁ и R_V − напряжение на вольтметре и его сопротивление; U₀-U₁=U_R – напряжение сопротивления R (рис. 17).

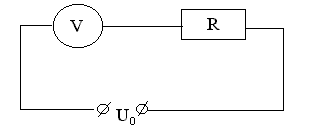
Для случая, когда включено неизвестное сопротивление,

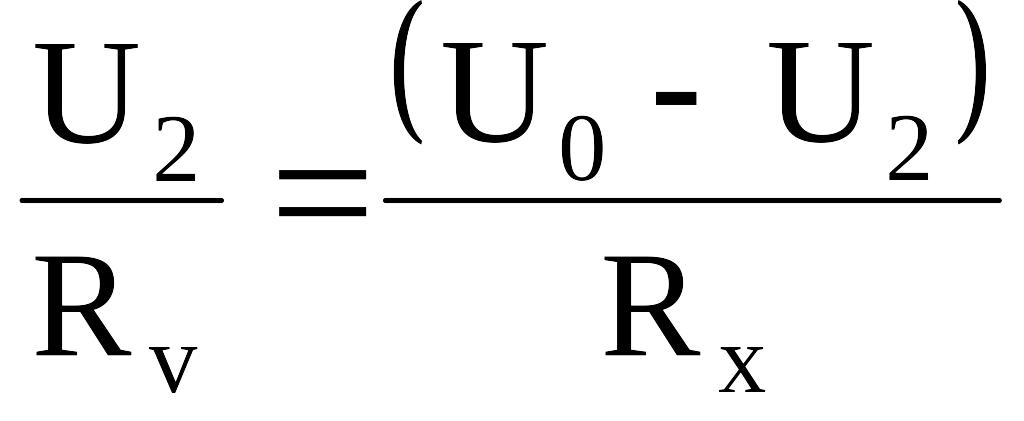. (2)

Исключив из (1) и (2) величину R_V, получим