- •Часть 1
- •Кинематика
- •Динамика материальной точки и тела, движущегося поступательно
- •Механика твёрдого тела
- •Механические колебания
- •Молекулярная физика
- •Физические основы термодинамики
- •Электростатика. Постоянный ток.
- •Закон сохранения заряда:
- •Напряженность и потенциал электростатического поля:
- •Теорема Остроградского-Гаусса. Поток вектора напряженности через любую замкнутую поверхность, охватывающую заряды q1, q2, …, qn, –
- •Объемная плотность энергии (энергия электрического поля, приходящаяся на единицу объема):
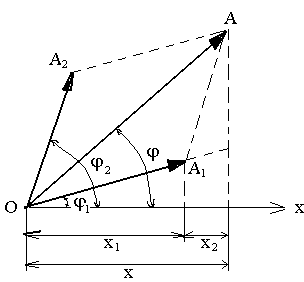
- •Согласно теореме косинусов, получим:
- •Решение. Воздух, являясь смесью идеальных газов, тоже представляет собой идеальный газ, и к нему можно применить уравние Менделеева–Клапейрона:
- •Решение. В основном уравнении молекулярно- кинетической теории –
- •Решение. Вычислим значения молярных теплоемкостей водорода, учитывая, что молекулы водорода – двухатомные, а число I степеней свободы равно пяти:
- •Используя условие задачи и уравнение для изобарического процесса
- •Решение. Поскольку совершается адиабатический процесс, для решения используем уравнение адиабаты в виде
- •Решение. Термический кпд тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу:
- •По формуле
- •Контрольные задания
- •Часть 2
- •Электромагнетизм.
- •Оптика. Атомная и ядерная физика
- •Контрольные задания
- •2. Некоторые внесистемные величины:
- •4. Молярные массы (м, 10-3 кг/моль) газов:
Объемная плотность энергии (энергия электрического поля, приходящаяся на единицу объема):
![]() ,
,
где Е – напряженность электрического поля в среде с диэлектрической проницаемостью ; D – электрическое смещение.
Сила постоянного тока –
![]()
где q – количество электричества, прошедшего через поперечное сечение проводника за время t.
Плотность электрического тока есть векторная величина, равная отношению силы тока к площади S поперечного сечения проводника:
![]() ,
,
где
![]() - единичный вектор, по направлению
совпадающий с движением положительных
носителей заряда.
- единичный вектор, по направлению
совпадающий с движением положительных
носителей заряда.
Сопротивление однородного проводника –
![]() ,
,
где - удельное сопротивление вещества проводника; – его длина.
Проводимость G проводника и удельная проводимость вещества определяются так:
![]() .
.
Зависимость удельного сопротивления от температуры –
=0 (1+t),
где и 0 – значения удельного сопротивления соответственно при t и 00С, где t – температура (по шкале Цельсия); - температурный коэффициент сопротивления.
Сопротивление соединения проводников рассчитывается следующим образом:
при последовательном соединении –
![]() ;
;
при параллельном соединении –
![]() ,
,
где Ri – сопротивление i-го проводника; n – число проводников.
Закон Ома:
для однородного участка цепи (12=0) –
![]() ;
;
для неоднородного участка цепи –
![]() ;
;
для замкнутой цепи –
![]() ,
,
где
![]() - разность потенциалов на концах участка
цепи; 12
– ЭДС источника тока, входящего в
участок; U
– напряжение на участке цепи; R
- сопротивление цепи (участка цепи);
- ЭДС всех источников тока цепи.
- разность потенциалов на концах участка
цепи; 12
– ЭДС источника тока, входящего в
участок; U
– напряжение на участке цепи; R
- сопротивление цепи (участка цепи);
- ЭДС всех источников тока цепи.
Правила Кирхгофа. Первое правило: алгебраическая сумма сил токов, сходящихся в узле, равна нулю, т.е.
![]() ,
,
где n – число токов, сходящихся в узле.
Второе правило: в замкнутом контуре алгебраическая сумма напряжений на всех участках контура равна алгебраической сумме величин электродвижущих сил, т.е.
![]() =
=![]() ,
,
где Ii – сила тока на i-ом участке; Ri – активное сопротивление на i-ом участке; I – ЭДС источников тока на i-ом участке; n – число участков, содержащих активное сопротивление; k – число участков, содержащих источник тока.
Работа, совершаемая электростатическим полем и сторонними силами на участке цепи постоянного тока за время t, –
![]() .
.
Мощность тока –
![]() .
.
Закон Джоуля-Ленца –
![]() ,
,
где Q – количество теплоты, выделяющейся на участке цепи за время t.
Закон Джоуля-Ленца справедлив при условии, если участок цепи неподвижен и в нем не происходят химические превращения.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид x = A + Bt + Ct3, где А =2 м, В = 7м/с; С = -0,5м/с3. Найти координату x, скорость v и ускорение a точки в момент времени t, равный 2 с.
Решение. Координату x найдем, подставив в уравнение движения числовые значения коэффициентов А,В,С и времени t:
x=(2+7∙2-0,5∙23)=12 м.
Мгновенная скорость есть первая производная от координат по времени:
v
=
![]() =
B
+3Ct2.
=
B
+3Ct2.
Ускорение точки найдем, взяв первую производную от скорости по вре- мени:
a
=
![]() =
6Ct2.
=
6Ct2.
В момент времени t=2с
v =(7-3∙0,5∙22) = 1м/с;
a = 6 · 0,5 ·2 = 6 м/с2.
Пример 2. Тело брошено со скоростью v0 = 10 м/с под углом α = 400 к горизонту. Пренебрегая сопротивлением воздуха, найти:
1) высоту h подъема тела; 2) дальность S полета тела (по горизонтали);
3)время движения тела.
Решение. Перемещение тела можно разложить на два: горизонтальное вдоль оси x и вертикальное вдоль оси y (см. рисунок). Применяя закон независимости движений, имеем
h
=
![]() ;
(1)
;
(1)
S = vox · 2t, (2)
где t – время подъема; 2t – время полета.
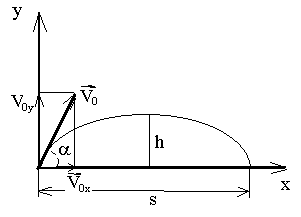
Из рисунка видно, что v0y =v0sinα; v0x = v0cosα . В верхней точке подъема vy = 0, и из уравнения vy = v0y – gt получаем, что v0sin α = gt. Отсюда время подъема равно
t
=![]() c.
c.
Подставив значение t в (1), получим высоту, на которую поднимется тело:
h=
![]() м.
м.
Подставив значение t в (2), найдем дальность полета:
S = v0 cosα 2t = 10·0,77·1,3 = 10м.
Время полета 2t = 2 · 0,64 = 1,3 с.
Пример 3. Диск радиусом R =5 см вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением
ω = 2At + 5Bt4, где А = 2 рад/с2, В = 1 рад/с5.
Найти для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов диска.
Решение.
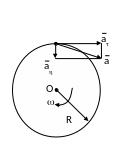
Полное ускорение может быть найдено
как геометрическая сумма тангенциального
ускорения
![]() ,
направленного по касательной к
траектории, и нормального ускорения
an,
направленного к центру кривизны
траектории, см. рисунок.
,
направленного по касательной к
траектории, и нормального ускорения
an,
направленного к центру кривизны
траектории, см. рисунок.
![]() .
.
|
Так
как векторы
где ε – угловое ускорение тела; ω – угловая скорость тела.
|
По условию задачи
ω = 2 Аt + 5 Bt4.
Следовательно,
![]() м/с2;
м/с2;
![]() м/с2.
м/с2.
Полное ускорение
![]() м/с2.
м/с2.
Угол поворота диска равен φ = 2πN (где N –число оборотов), но угловая скорость составляет
![]() .
.
Следовательно,
![]() .
.
Тогда число оборотов диска –
![]() .
.
Пример 4. Маховик вращается с постоянной частотой n0=10 c-1. При торможении он начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой n = 6c-1. Найти угловое ускорение ε маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N=50 оборотов.
Решение.
Угловое ускорение маховика связано с
начальной
![]() и конечной ω угловыми скоростями
соотношением
и конечной ω угловыми скоростями
соотношением
![]() ;
откуда
;
откуда
![]()
Но так как φ = 2 π N, ω = 2 π n, то
![]() рад/с2.
рад/с2.
Знак «минус» указывает на то, что маховик вращается замедленно.
Для определения продолжительности торможения используем формулу, связывающую угол поворота со средней угловой скоростью вращения и временем: φ = ωсрt. По условию задачи угловая скорость линейно зависит от времени, и поэтому ср можно выразить так:
![]() ,
,
тогда
![]() .
Откуда
.
Откуда
![]() с.
с.
Пример
5.
К
нити подвешен груз массой m=1
кг. Найти силу натяжения нити
![]() ,
если нить с грузом: 1) поднимать с
ускорением a=5
м/с2;
2) опускать с тем же ускорением.
,
если нить с грузом: 1) поднимать с
ускорением a=5
м/с2;
2) опускать с тем же ускорением.
Р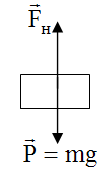 ешение.
ешение.
На
поднимаемый груз, действуют сила тяжести
mg
(вниз) и сила натяжения нити FH
(вверх), см. рисунок. Применив второй
закон Ньютона, получим, что ma=FH-mg.
Отсюда
![]() H.
H.
На
опускаемый груз также действуют сила
тяжести mg
(вниз) и сила натяжения нити FH
(вверх).
Применив второй закон Ньютона, получим,
что
![]() .
Отсюда
.
Отсюда
![]() H.
H.
Пример 6. По плоскости с углом наклона 300 к горизонту скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения k = 0,15.
Решение
У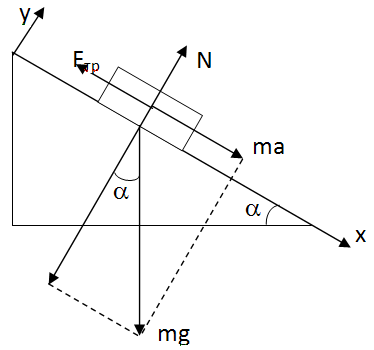 равнение
движения тела в векторной форме (второй
закон Ньютона):
равнение
движения тела в векторной форме (второй
закон Ньютона):
![]() .
.
В проекциях на оси x и y это уравнение примет вид
![]() ;
(1)
;
(1)
![]() .
(2)
.
(2)
И з
уравнения (2)
з
уравнения (2)
![]() ,
см. рисунок. Сила трения
,
см. рисунок. Сила трения
![]() .
.
Тогда,
подставив
![]() в уравнение (1), получим выражение
в уравнение (1), получим выражение
mgsinα-kmgcosα=ma,
отсюда a=g(sinα-kcosα).
Скорость
тела
![]() ,
но v0=0;
поэтому
,
но v0=0;
поэтому
![]() м/с.
м/с.
Пример 7. Шар массой m1, движущийся горизонтально с некоторой скоростью v1, столкнулся с неподвижным шаром массой m2. Шары – абсолютно упругие, удар прямой. Какую долю своей кинетической энергии первый шар передал второму?
Решение. Доля энергии, переданной первым шаром второму, выразится соотношением
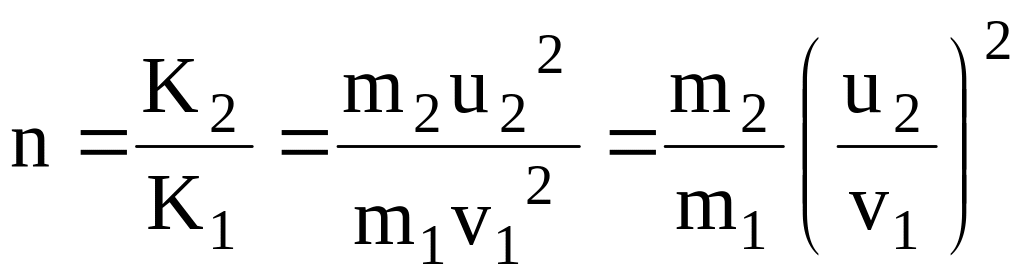 ,
(1)
,
(1)
где K1 – кинетическая энергия первого шара до удара; u2 и K2 – скорость и кинетическая энергия второго шара после удара.
При ударе абсолютно упругих тел одновременно выполняются два закона сохранения: импульса и механической энергии. По закону сохранения импульса, с учетом того, что второй шар до удара покоился, имеем
![]() .
.
По закону сохранения механической энергии –
![]() .
.
Решая совместно два последних уравнения, найдём, что
![]() .
.
Подставив выражение в равенство (1), получим
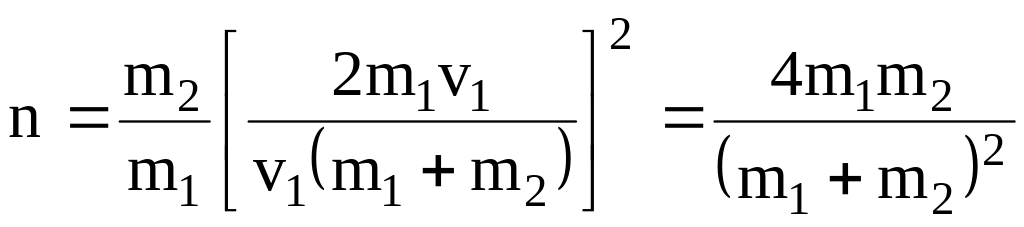 .
.
Из этого соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.
Пример
8.
Сплошной
шар массой 1 кг и радиусом 0,05 м вращается
вокруг оси, проходящей через его центр.
В точке, наиболее удалённой от оси
вращения, на шар действует сила,
касательная к поверхности. Угол поворота
шара меняется по закону
![]() .
Определить величину действующей силы,
тормозящий момент, время равнозамедленного
движения.
.
Определить величину действующей силы,
тормозящий момент, время равнозамедленного
движения.
Решение. Согласно основному закону динамики вращательного движения вращающийся момент равен , где J – момент инерции шара; ε – угловое ускорение. Момент инерции шара:
![]() .
.
Угловое
ускорение –
![]() .
.
С ледовательно,
ледовательно,
![]() .
.
![]()
![]() ,
где
,
где
![]() -
радиус – вектор, проведённый из этой
точки в точку
приложения силы. Модуль момента
-
радиус – вектор, проведённый из этой
точки в точку
приложения силы. Модуль момента
силы,
как видно из рисунка,
![]() .
Отсюда
.
Отсюда
![]() .
.
В момент остановки шара ω=0,
![]()
Пример 9. Найти линейное ускорение шара, скатывающегося без скольжения с наклонной плоскости. Угол наклона плоскости =300, начальная скорость v0=0.
Решение. При скатывании шара с наклонной плоскости высотой h его потенциальная энергия уменьшается, переходя в кинетическую поступательного и
вращательного движения:
![]() ,
(1)
,
(1)
где
J
– момент инерции шара. Так как
![]() и
и
![]() ,
где R
– радиус шара, то уравнение (1) можно
записать так:
,
где R
– радиус шара, то уравнение (1) можно
записать так:
![]() ,
,
т.е.
![]() .
.
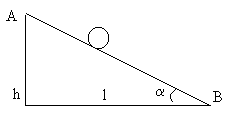
Из
рисунка видно, что h=lsinα;
тогда
![]() ;
;
![]() .
(2)
.
(2)
Так как движение тела происходит под действием постоянной силы, то оно равноускоренное с v0=0 (из условия задачи); поэтому
![]() .
(3)
.
(3)
Подставив (3) в уравнение (2), получим:
![]() м/с2.
м/с2.
Пример
10.
Маховик
в виде диска массой m=50
кг и радиусом R
= 20 см был раскручен до частоты вращения
![]() .
Вследствие трения маховик остановился.
Найти момент M
сил трения, считая его постоянным для
двух случаев: 1) маховик остановился
через t=50
с; 2) маховик до полной остановки сделал
N=200
об.
.
Вследствие трения маховик остановился.
Найти момент M
сил трения, считая его постоянным для
двух случаев: 1) маховик остановился
через t=50
с; 2) маховик до полной остановки сделал
N=200
об.
Решение. По основному закону динамики вращательного движения изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента:
![]() ,
,
где
J
–момент инерции маховика;
и
- начальная и конечная угловые скорости.
Так как ω2=0
и
![]() ,
то Mt=-Jω,
откуда
,
то Mt=-Jω,
откуда
![]() .
(1)
.
(1)
Момент инерции диска относительно его геометрической оси равен
![]() .
.
Подставив это выражение в формулу (1), найдём, что
![]() .
(2)
.
(2)
Выразив
угловую скорость ω1
через частоту вращения
![]() ,
получим
,
получим
![]() ,
произведя вычисления по формуле (2),
найдём, что
,
произведя вычисления по формуле (2),
найдём, что
![]() .
.
В условии задачи дано число оборотов маховика до остановки, т.е. его угловое перемещение:
![]() рад.
рад.
Запишем формулу, выражающую связь работы с изменением кинетической энергии:
![]() ,
или ω2=0.
,
или ω2=0.
Она примет вид
![]() .
(3)
.
(3)
Работа при вращательном движении определяется по формуле . Подставив выражение работы и момента инерции диска в формулу (3), получим
![]() .
.
Отсюда
![]() =
–1 (Нм) .
=
–1 (Нм) .
Знак «минус» показывает, что момент силы трения оказывает тормозящее действие.
Пример
11.
Человек
стоит в центре круга Жуковского,
вращающегося по инерции вокруг неподвижной
оси с частотой
![]() .
В вытянутых руках он держит по гире
массой m=5кг
каждая. Расстояние от каждой гири до
оси вращения
.
В вытянутых руках он держит по гире
массой m=5кг
каждая. Расстояние от каждой гири до
оси вращения
![]() Суммарный момент инерции человека и
скамьи относительно оси вращения I0=2
кгсм2.
Определить частоту n2
вращения скамьи с человеком. Какую
работу совершит человек, если прижмёт
гири к себе так, что расстояние от каждой
гири до оси станет равным
2=20cм?
Суммарный момент инерции человека и
скамьи относительно оси вращения I0=2
кгсм2.
Определить частоту n2
вращения скамьи с человеком. Какую
работу совершит человек, если прижмёт
гири к себе так, что расстояние от каждой
гири до оси станет равным
2=20cм?
Решение. По условию задачи момент внешних сил относительно вертикальной оси вращения равен нулю, поэтому момент импульса системы сохраняется:
I1ω1= I2 ω2,
где
![]() – соответственно момент инерции всей
системы до и после сближения; m-
масса каждой гири. Угловая скорость
ω=2πn.
Подставив
в уравнение, получим искомую частоту
вращения:
– соответственно момент инерции всей
системы до и после сближения; m-
масса каждой гири. Угловая скорость
ω=2πn.
Подставив
в уравнение, получим искомую частоту
вращения:
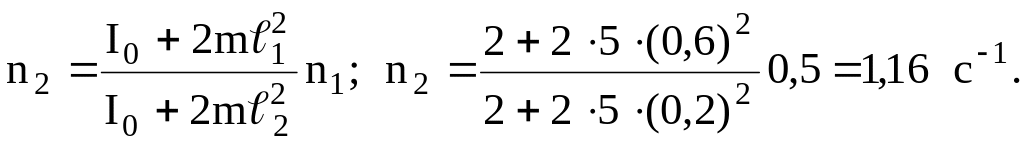
Работа, совершаемая человеком, равна изменению кинетической энергии системы:
![]() .
.
Пример 12. Материальная точка массой m=10 г совершает гармонические колебания частотой = 0,2 Гц. Амплитуда колебаний равна 5 см. Определить: а) максимальную силу, действующую на точку; б) полную энергию колеблющейся точки.
Решение. Уравнение гармонического колебания: х= A cos (ω0t+ φ).
Тогда скорость и ускорение колеблющейся точки находятся так :
![]() ;
;
![]()
Согласно второму закону Ньютона сила, действующая на точку, –
![]() при
при
![]() .
.
Поэтому искомое максимальное значение силы (с учетом того, что ω0= 2π) будет равно
![]() .
.
Полная энергия колеблющейся точки –
![]() мкДж.
мкДж.
Пример
13.
Складываются два колебания одинакового
направления, выражаемые уравнениями
![]() и
и
![]() ,
где А1=1см,
А2=2см,
τ1=
,
где А1=1см,
А2=2см,
τ1=![]() с,
с,
![]() с,
с,
![]() .
.
Определить начальные фазы φ01, φ02 составляющих колебаний и амплитуду результирующего колебания.
Решение. Уравнение гармонического колебания имеет вид
x = Acos(ωt+φ).
x1=A1cos(ωt+ωτ1), x2 =A2cos(ωt+ ωτ2).
Тогда:
![]()
Для определения амплитуды результирующего колебания представим векторную диаграмму, см. рисунок.