4. Линия

Кинематическое определение линии может быть следующим:

линия - это множество всех последовательных положений движущейся точки.

Не вникая в классификацию всех существующих линий, выделим те, с спорыми в дальнейшем чаще всего придётся иметь дело:

• прямые (движущаяся точка не изменяет направления своего движения);

• ломаные (звенья ломаных - отрезки прямых);

• замкнутые (движущаяся точка периодически возвращается в исходное положение);

- разомкнутые (движущаяся точка не возвращается в исходное положение);

• кривые (движущаяся точка изменяет направление своего движения);

• плоские (все точки таких линий принадлежат одной плоскости);

• пространственные (все точки их не принадлежат одной плоскости). Кроме этих важнейших линий имеются и другие разновидности линий

алгебраические, трансцендентные, графические и т.д.).

Прямую линию можно задать двумя точками.

Как задавать одну точку и изображать её на комплексном чертеже, мы уже знаем. Задав так же вторую точку и соединив их отрезком, получим прямую, проекция которой на чертеже будет выглядеть так, как показано на рис.4, где отрезок АВ задает направление прямой (напомним, что сама прямая в пространстве бесконечна).

В зависимости от расположения той или иной прямой по отношению к плоскостям проекций различают прямые:

• общего положения;

• частного положения.

Прямая общего положения - не параллельна и не перпендикулярна ни одной из плоскостей проекций. Примером такой прямой является изображенный отрезок прямой АВ.

Прямые частного положения бывают следующими:

• прямые уровня;

• проецирующие прямые.

Первые из них параллельны одной из плоскостей проекций, а вторые перпендикулярны одной из этих плоскостей. Этим и определяются их названия:

горизонталь - прямая, параллельная горизонтальной плоскости проекций (прямая горизонтального уровня).

фронталь - прямая, параллельная фронтальной плоскости проек­ций (прямая фронтального уровня).

профильная прямая - прямая, параллельная профильной плоскости проекций (прямая профильного уровня).

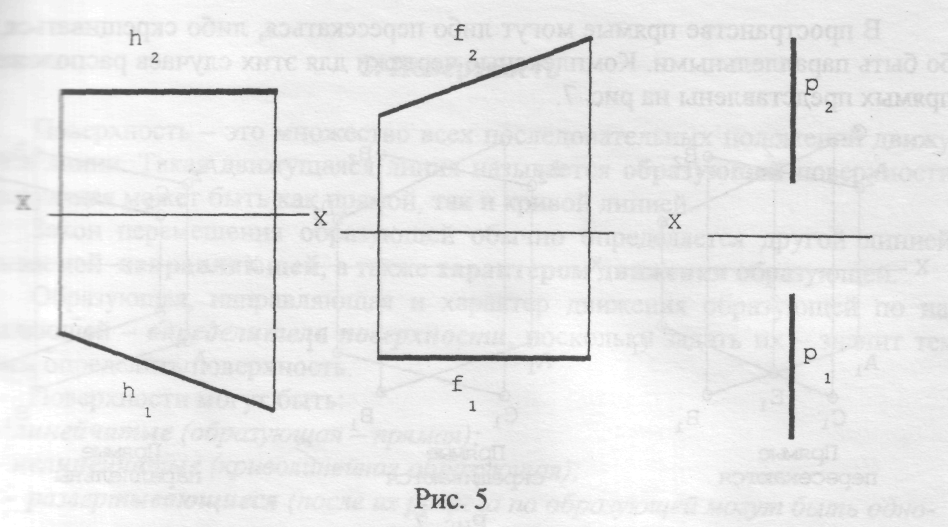
На чертеже они выглядят так как показано на рис. 5, где:

h₂ – фронтальная проекция горизонтали;

h₁ – горизонтальная проекция горизонтали;

f₂ - фронтальная проекция фронтали;

f₁ – горизонтальная проекция фронтали;

p₁, p₂ – соответствующие проекции профильной прямой.

Поскольку проецирующая прямая перпендикулярна к какой-либо из плоскостей проекций, проекция прямой на ту плоскость проекций, к которой она перпендикулярна, представляет собой точку (главная проекция). Среди проецирующих прямых (рис. 6) различают:

• фронтально-проецирующие (рис. 6а);

• горизонтально-проецирующие (рис. 66);

• профильно-проецирующие (рис. 6в).

Нужно заметить, что проецирующие прямые одновременно являются и прямыми уровня. Фронтально-проецирующая прямая, например, - одновременно и горизонталь, и профильная прямая, поскольку она параллельна и горизонтальной, и профильной плоскостям проекций. По этим же причинам горизонтально-проецирующая прямая - фронталь и профильная прямая, а профильно-проецирующая прямая - горизонталь и фронталь. То есть, проецирующие прямые одновременно являются дважды прямыми уровня.

В пространстве прямые могут либо пересекаться, либо скрещиваться, либо быть параллельными. Комплексные чертежи для этих случаев расположения прямых представлены на рис. 7.

Кривая линия чаще всего может быть задана своими проекциями (рис. 8)

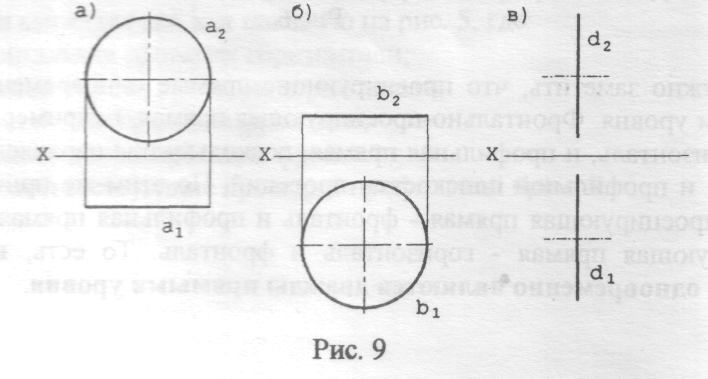
Наибольший же интерес представляет изображение окружностей, располагающихся в плоскостях, параллельных одной из основных плоскостей проекций. На рис. 9 представлены двухпроекционные комплексные чертежи для ок­ружностей, плоскости которых параллельны фронтальной (рис. 9а), горизонтальной (рис. 9б) и профильной (рис. 9в) плоскостям проекций.