2. Свойства прямоугольного проецирования

Сформулируем эти свойства.

1. Точка проецируется в точку.

2. Прямая проецируется в прямую (в общем случае).

3. Если точка принадлежит прямой, то и проекция точки принадлежит проекции прямой.

4. Если прямые параллельны, то их проекции параллельны.

5. Отношение отрезков прямой равно отношению проекций этих отрезков.

6. Отношение отрезков параллельных прямых равно отношению проекций этих отрезков.

7. Проекция геометрической фигуры по величине и форме не изменяется при параллельном перемещении плоскости проекций.

8. Проекция отрезка не может быть больше самого отрезка. Доказательство всех этих свойств можно найти в литературе. Еще одно важное свойство будет сформулировано ниже.

3. Комплексный чертеж. Точка

Проекционные изображения, используемые в технической документации, должны обладать следующими свойствами:

• быть наглядными;

• обладать простотой графического выполнения;

• быть обратимыми, то есть такими, чтобы по ним можно было

представить сам предмет и в дальнейшем его изготовить.

Наличие одной проекции создает неопределенность изображения. Поэтому в практике однопроекционные изображения дополняют. Одним из таких дополнений являются комплексные изображения. Они получаются, если предмет с помощью прямоугольного проецирования проецируют на три взаимно перпендикулярных плоскости проекции. Этот способ впервые был предложен, систематизирован и описан французским ученым Г.Монжем, поэтому его иногда называют методом Монжа.

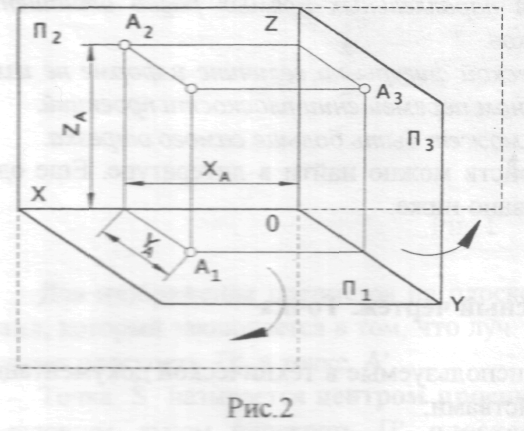
Три взаимно перпендикулярные плоскости, на которые производят проецирование какого-либо предмета или точки, дают три изображения, а также некоторую систему координат ОХУZ, где положение любой точки определяется однозначно, тремя её проекциями: А (Х_А, Y_A, Z_A).

Обычно рассматривают предмет, расположенный в пространстве трех плоскостей, образующих так называемый "правый" угол.

Вообще говоря, три плоскости П₁-П₂-П₃ делят пространство на 8 частей (октантов). Здесь показан один октант, где все координаты точки А (Х_А, У_А, Z_A) - положительны.

Плоскости называют:

П₁ - горизонтальная плоскость проекций,

П₂ - фронтальная плоскость проекций, П₃ - профильная плоскость проекций.

В связи с этим проекции любой точки на эти плоскости снабжаются соответствующим индексом -1,2 или 3 (рис.2).

Чтобы изображение предмета, спроецированное на три плоскости проекций, изобразить на одной плоскости, мысленно производят разрез по оси ОY и поворачивают плоскость П₁ вокруг оси ОХ, а плоскость П₃ - вокруг оси ОZ для совмещения с плоскостью П₂, получая изображение показанное на рис. 3.

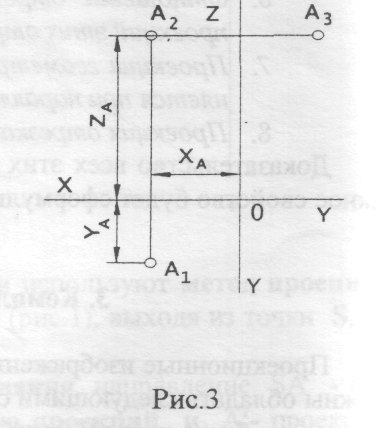
Линии А₁А₂ и А₂А₃ называют линиями проекционной связи (или просто линиями связи). У А₁А₂ ┴ X и А₂А₃ ┴ Z, поскольку проецирование прямоугольное.

Основные свойства трсхпроекционного комплексного чертежа, приведенного на рис.3:

- две проекции точки принадлежат одной линии связи;

- линия связи перпендикулярна к соответствующей оси проекций;

- две проекции тючки определяют ее третью проекцию.

Таким образом, Комплексный чертеж - это изображение на одной плоскости нескольких взаимных прямоугольных проекций предмета, полученное после определенного совмещения плоскостей проекции с плоскостью чертежа.

Двухпроекционный комплексный чертеж состоит из изображений предметов на двух, плоскостях проекций, совмещенных с плоскостью чертежа. Им удобно пользоваться, поскольку две любых проекции предмета или точки всегда содержат все три их координаты, однозначно определяющих положение предмета или точки в пространстве. Другими словами, и в этом случае чертеж будет обратимым. Следовательно, имея проекции какого-то предмета, можно однозначно представить его в натуре.

Чтобы закончить все о точке, отметим, что

точки, лежащие на одном проецирующем луче, называются конкурирующими точками (это, например, точки А и К на рис. 1). Это обстоятельство лежит в основе метода конкурирующих точек, используемого для определения видимости проекций линий и плоских фигур.