9. Связь криволинейного интеграла 2 рода по замкнутому контуру с двойным интегралом по области, ограниченной этим контуром (формула Грина)
Пусть
- простая область и пусть функции
и
непрерывны вместе со своими частными
производными
и
в замкнутой области
.
Тогда имеет место формула Грина
.
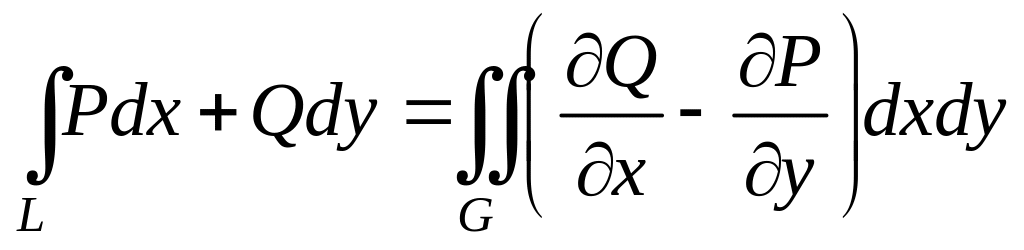Умения
4. Связь криволинейного интеграла 2-го рода по замкнутому контуру с двойным интегралом по области, ограниченной этим контуром.
Свести криволинейный интеграл 2 рода к двойному.
Решение:
Воспользуемся формулой Грина-Остроградского:
.
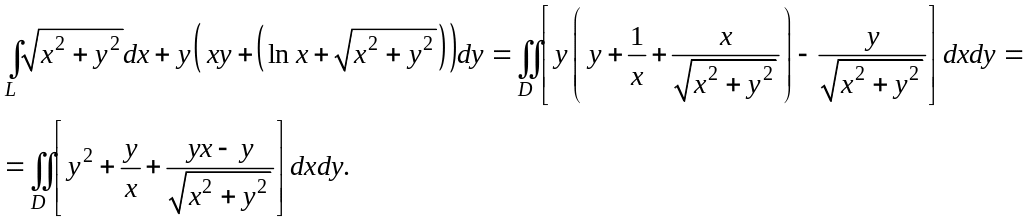
Ответ:
21. Условия независимости криволинейного интеграла второго рода от пути интегрирования
Понятия
6. Интеграл называется независимым от пути интегрирования, когда его значение не зависит от пути обхода кривой.
Из двух возможных направлений обхода замкнутого контура кривой, назовем положительным то направление обхода, при котором область, лежащая внутри этого контура, остается по левую сторону по отношению к точке, совершающей обход.
Утверждения
11. Три условия независимости криволинейного интеграла 2 рода от пути интегрирования
1. Для того чтобы криволинейный интеграл 2-го рода не зависел от пути интегрирования, необходимо и достаточно, чтобы криволинейный интеграл по любому замкнутому контуру был равен нулю.
2. Если функции
и
,
кривая
и область
удовлетворяют условия функции Грина,
тогда для того чтобы криволинейный
интеграл 2-го рода не зависел от пути
интегрирования, необходимо, а в случае
односвязной области
,
достаточно чтобы для всех точек
выполнялось равенство
.
3. Для того чтобы криволинейный интеграл 2-рода не зависел от пути интегрирования, необходимо и достаточно, чтобы подынтегральное выражение представляло полный дифференциал функции.
22. Вычисление криволинейного интеграла второго рода в случае, когда интеграл не зависит от пути интегрирования
Умения
5. Вычисление криволинейного интеграла 2-го рода в случае, когда интеграл не зависит от пути интегрирования.
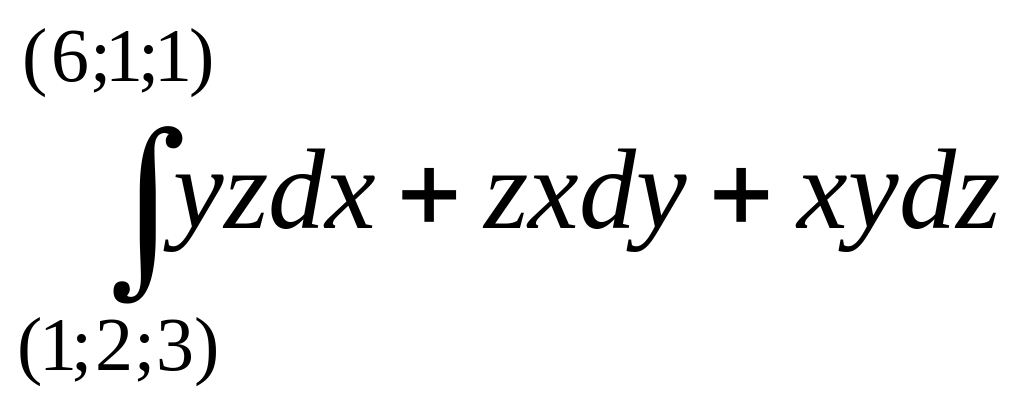
Решение:
Подынтегральная функция является полным
дифференциалом функции
,
следовательно, она не зависит от пути
интегрирования и интеграл равен:
.
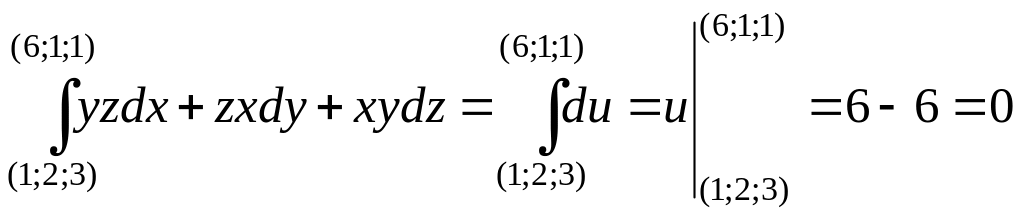Ответ: 0.
III. Приложения криволинейных интегралов
23. Полный дифференциал функции
Умения
13. Нахождение функции по ее полному дифференциалу:
Найти функцию
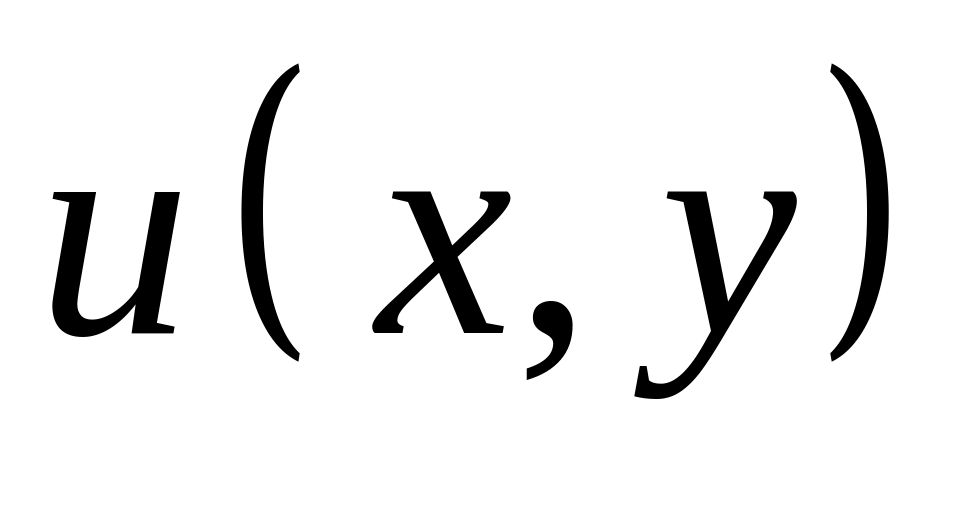по ее полному дифференциалу
.
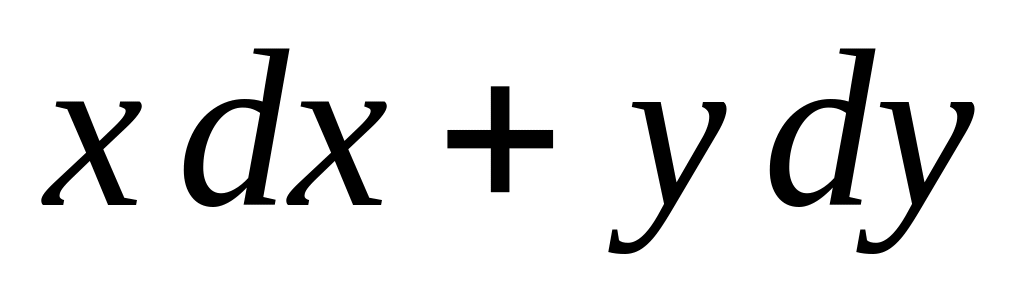Решение:
Определим полным дифференциалом какой функции является данное выражение.
,
,
откуда
,
но тогда
,
,
где С – некоторая константа, тогда
.
Ответ: , где С – константа.
Если
,
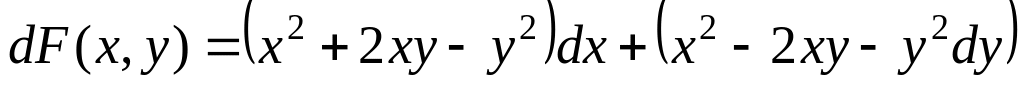то значение
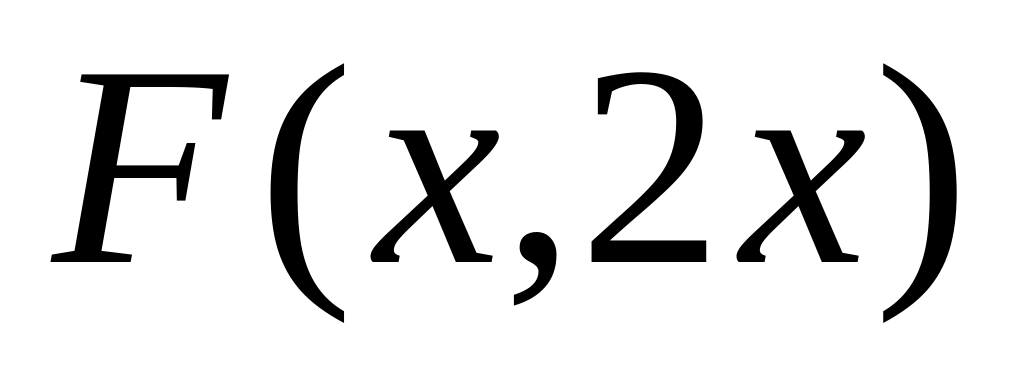равно
Решение:
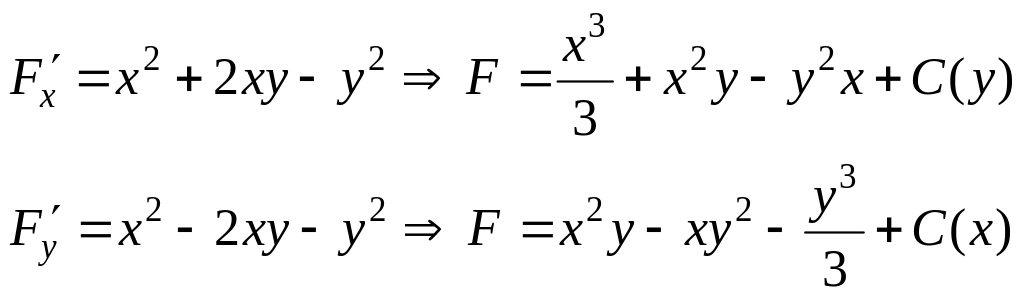следовательно,
Ответ:
,
где С – константа.
24. Нахождение площади плоской фигуры Умения
12. Интегрирование полных дифференциалов.
Найти криволинейный интеграл
.
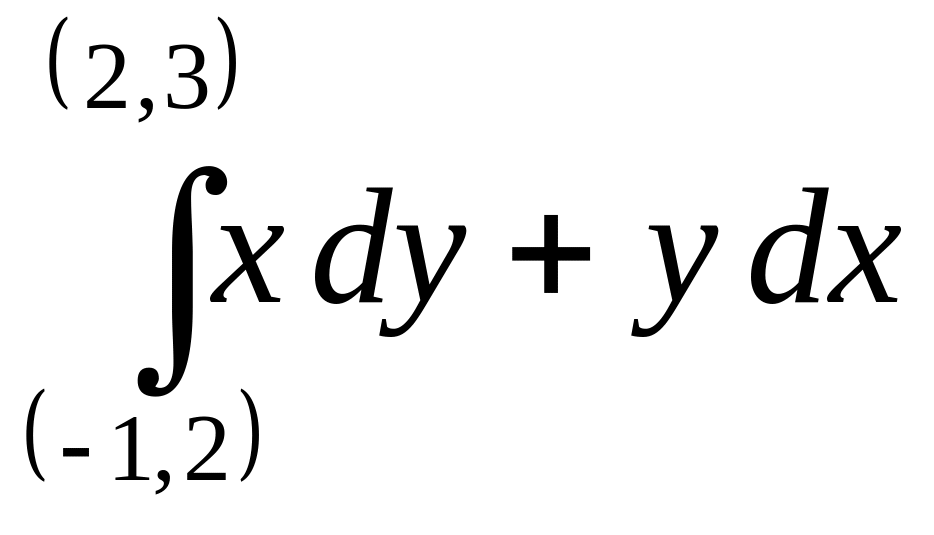Решение:
Сначала проверим, является ли данное
выражение под интегралом дифференциалом
некоторой функции.
,
откуда получаем, что данный интеграл
не зависит от пути интегрирования.
Если
,
то
,
откуда получаем, что
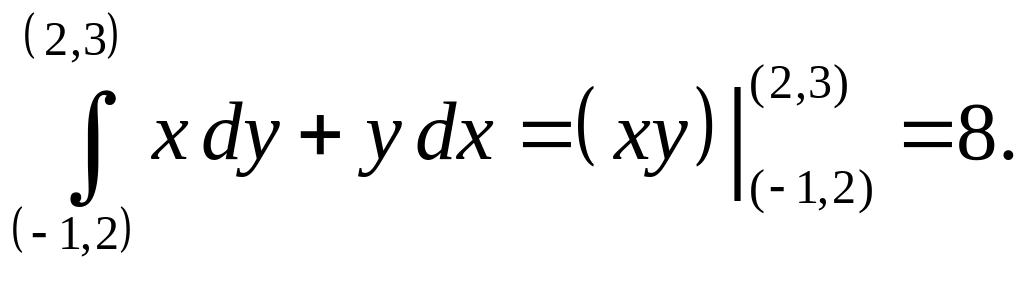
Ответ: 8.
Найти криволинейный интеграл
.
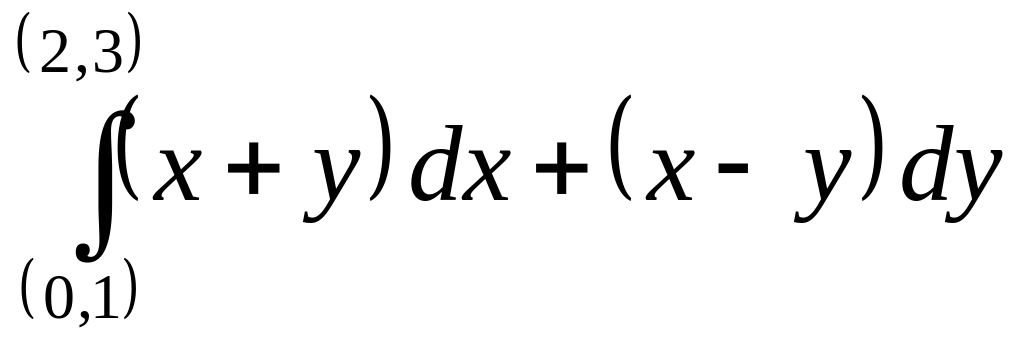Решение:
Сначала проверим, является ли данное
выражение под интегралом дифференциалом
некоторой функции.
,
откуда получаем, что данный интеграл
не зависит от пути интегрирования. Тогда
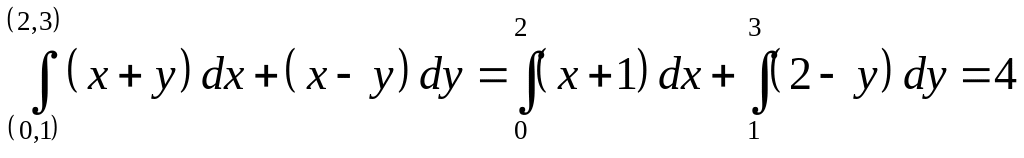
Ответ: 4.