С Т А Т И К А КОРАБЛЯ

МОДУЛЬ 5.8

3.16 Изменение посадки и остойчивости судна

при переносе, приеме и расходовании груза.

Понятие о нейтральной плоскости.

Перенос, прием и расходование грузов являются повседневными операциями в процессе эксплуатации судна. Такие операции приводят к изменению посадки (средней осадки, углов крена и дифферента) и остойчивости судна. Как правило, это изменение с достаточной для практики точностью можно оценить по формулам начальной остойчивости. Пересчет диаграмм статической и динамической остойчивости проводят лишь в случаях, связанных главным образом с обеспечением безопасности плавания .

Для простоты и наглядности рассмотрим вопрос в рамках теории начальной остойчивости.

1. Перенос груза

Пусть на судне некоторый груз P массой m перенесен так, что ЦТ этого груза переместился из точки с координатами x₀, y_­0, z₀ в точку с координатами x₁, y_­1, z₁. Тогда масса всего судна не изменится, но изменится положение его ЦТ. Разлагая фактическое перемещение ЦТ груза на три взаимно перпендикулярных перемещения, параллельные координатным осям, рассматриваем продольное перемещение l_x = x₁ — x₀ поперечное перемещение l_y = y₁ — y₀ и вертикальное перемещение l_z = z₁ — z₀.

Перемещение ЦТ судна можно найти с помощью теоремы теоретической механики о статических моментах, согласно которой

; ; (1)

Благодаря этому перемещению появятся две дополнительные пары сил. Одна из них будет действовать в ДП, вызывая дифферент. Плечо ее будет равно . Другая же будет действовать в поперечной плоскости, параллельной плоскости мидель-шпангоута, вызывая крен. Плечо ее будет равно (рис. 1). Моменты этих пар равны:

дифферентующий

;

кренящий

.

Рис. 1. Кренящая пара сил при переносе груза

Подставляя в эти формулы выражения (1), получим

(2)

Будем считать, что углы наклонения судна достаточно малы, так что ; ; . Это возможно в случае, когда сила тяжести переносимого груза P достаточно мала или малы перемещения l_x и l_y его ЦТ. Тогда формулы (2) принимают вид:

(3)

Согласно условиям равновесия действие этих моментов уравновесится действием восстанавливающих моментов. Определим последние по метацентрическим формулам остойчивости :

; . (4)

Отсюда угол дифферента, возникающий вследствие переноса груза, равен

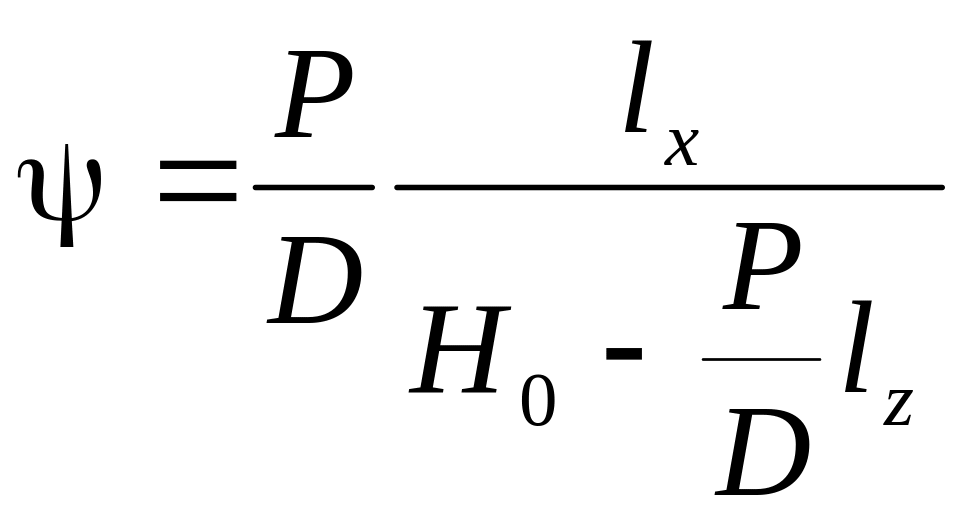, (5)

а угол крена

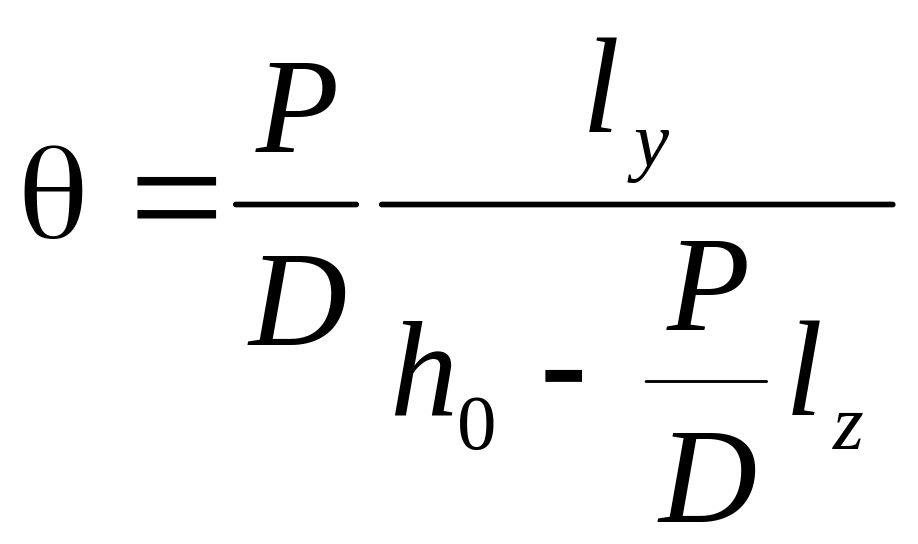. (6)

Выражения для метацентрических высот, измененные из-за влияния переноса груза, будут следующие:

; (7)

, (8)

где поправки к метацентрическим высотам оказываются одинаковыми;

.

Для большинства судов продольная метацентрическая высота много больше поперечной. Поэтому в практических расчетах поправкой почти всегда можно пренебречь по сравнению с и положить . Тогда, подставив (7) и (8) в формулы (5) и (6), окончательно найдем

; (9)

Если груз переносится в нос, то , , а значит и , т. е. судно получает дифферент на нос. Если же груз переносится в корму, то , , , т. е. судно дифферентует на корму. В случае переноса груза на правый борт и , а в случае переноса на левый и .