С т а т и к а корабля модуль 5.7

3.13. Динамическая остойчивость. Плечо динамической остойчивости

Работа, произведенная при наклонении судна , будет зависеть от изменения вертикального расстояния между центром тяжести и центром величины , т.е. работа будет производиться при подъеме веса D над центром величины. Она будет равна

T=Dd , (1)

где d - изменение расстояния по высоте между ЦТ и ЦВ, или иначе, плечо динамической остойчивости.

С другой стороны, работу восстанавливающего момента можно определить как

(2)

Приравняем (1) и (2) . Тогда получим

и

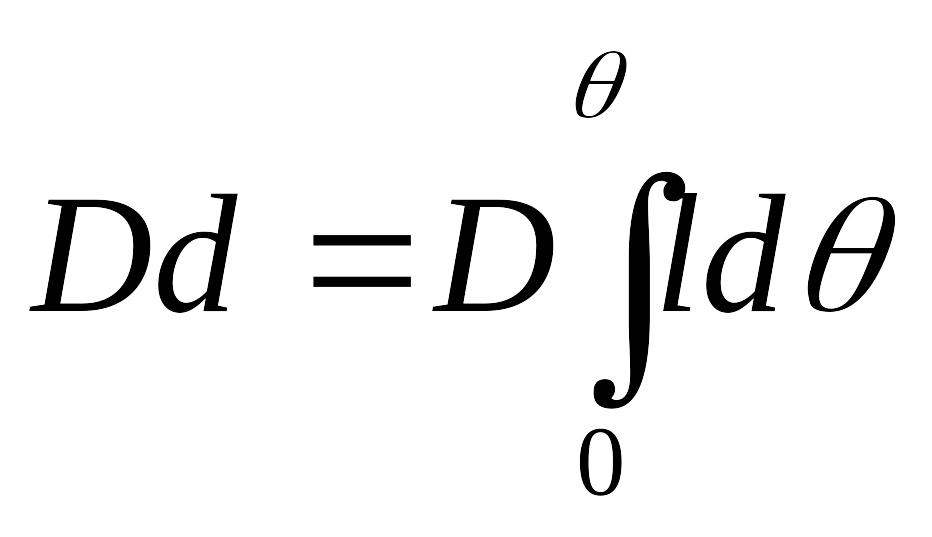
, (3)

т.е. плечо динамической остойчивости равно определенному интегралу от плеча статической остойчивости.

Из формулы (3) следует, что

(4)

и

. (5)

Величину d можно получить также графически (рис.1 ), если от точки К отложить по линии величину а. Тогда расстояние будет характеризовать изменение расстояния по высоте между ЦТ и ЦВ, т. е.

По построению ,

где .

Окончательно:

. (6)

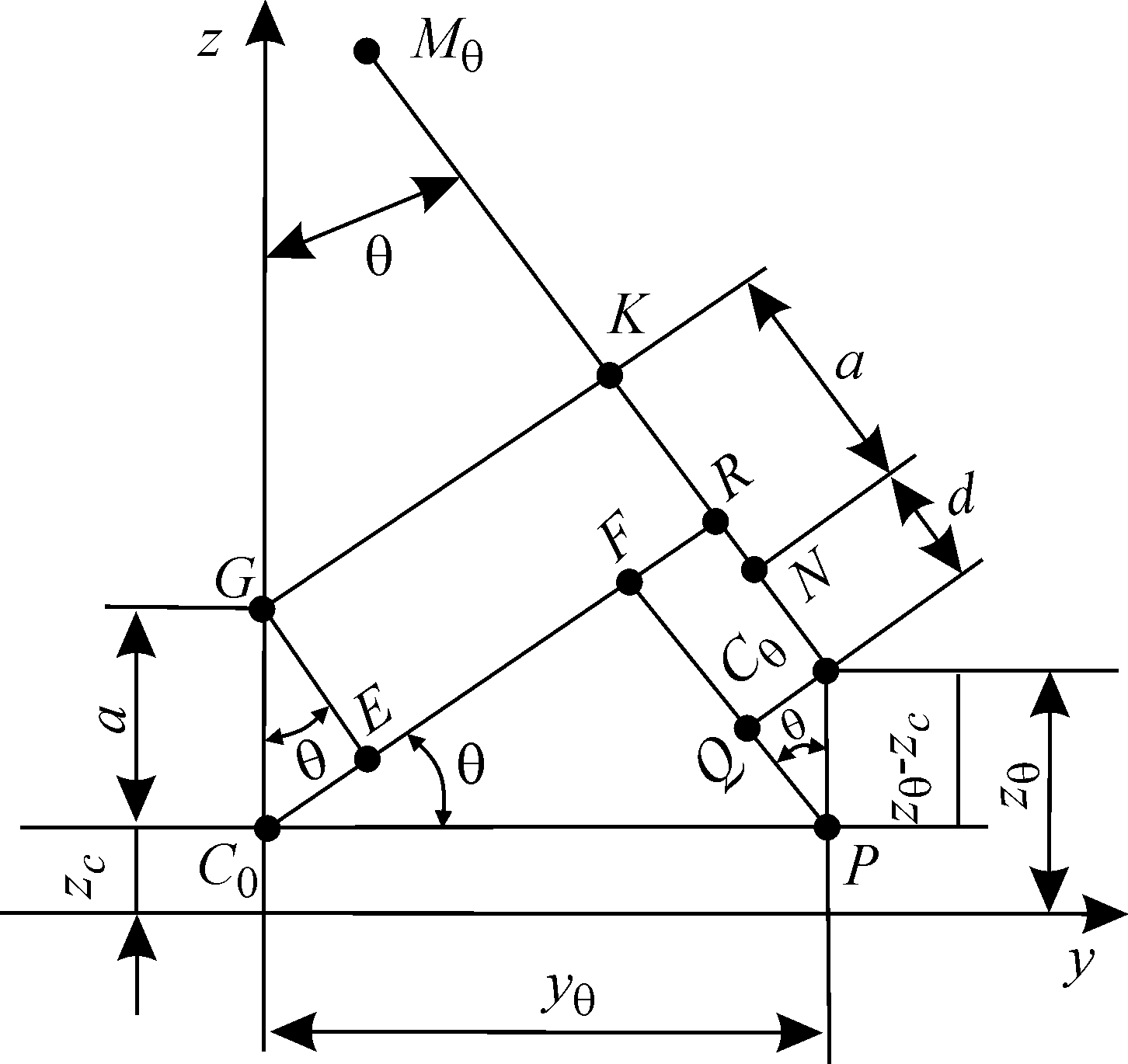
Рис.1

Если построить кривую d (θ), получится диаграмма динамической остойчивости, связанная с диаграммой статической остойчивости интегральной зависимостью (рис.2). Если на диаграмме динамической остойчивости провести при угле θ касательную к кривой d и отложитъ по горизонтали 1 рад, получится плечо статической остойчивости l, соответствующее углу θ (рис.3)

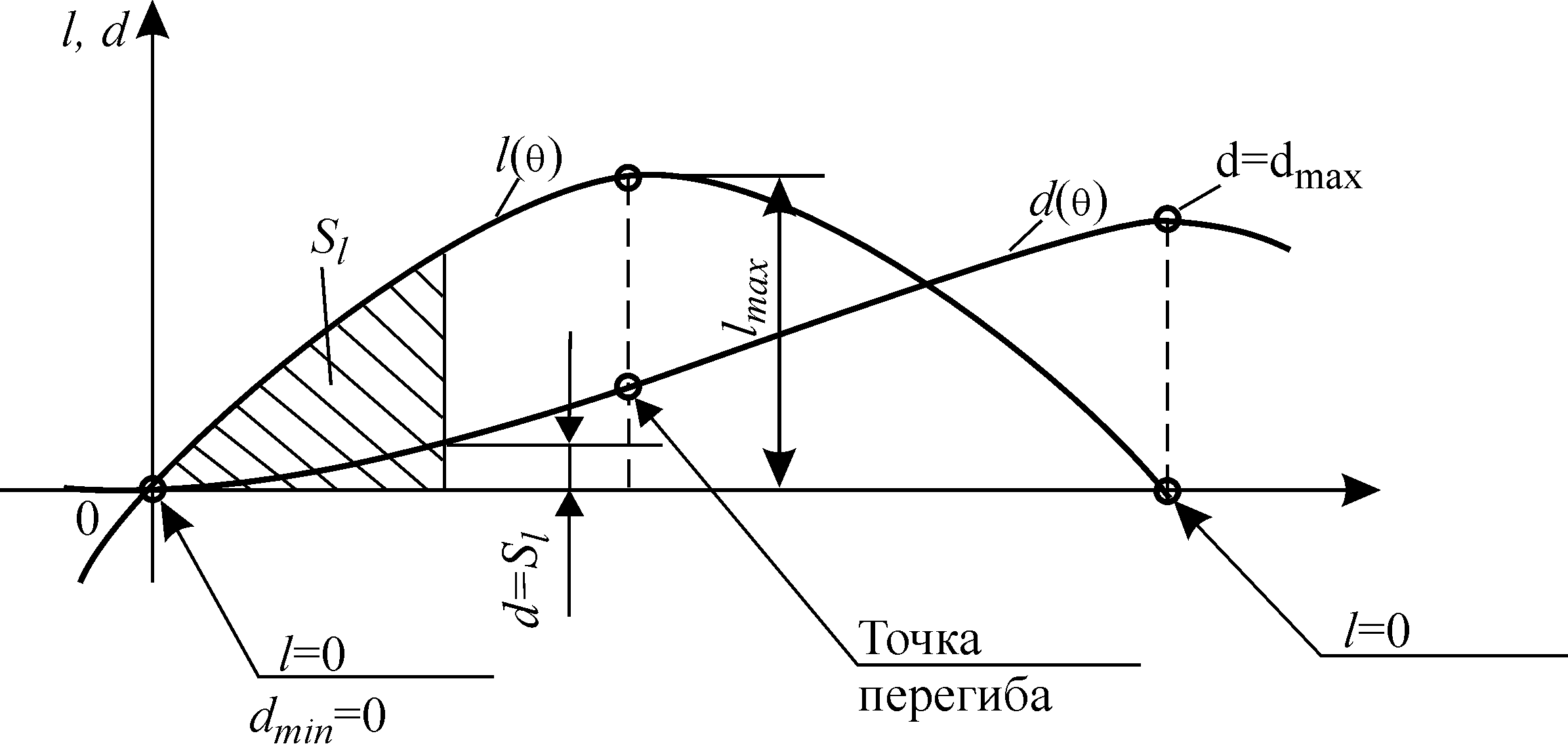
Рис.2.Диаграммы динамической и статической остойчивости при поло-жительной h₀

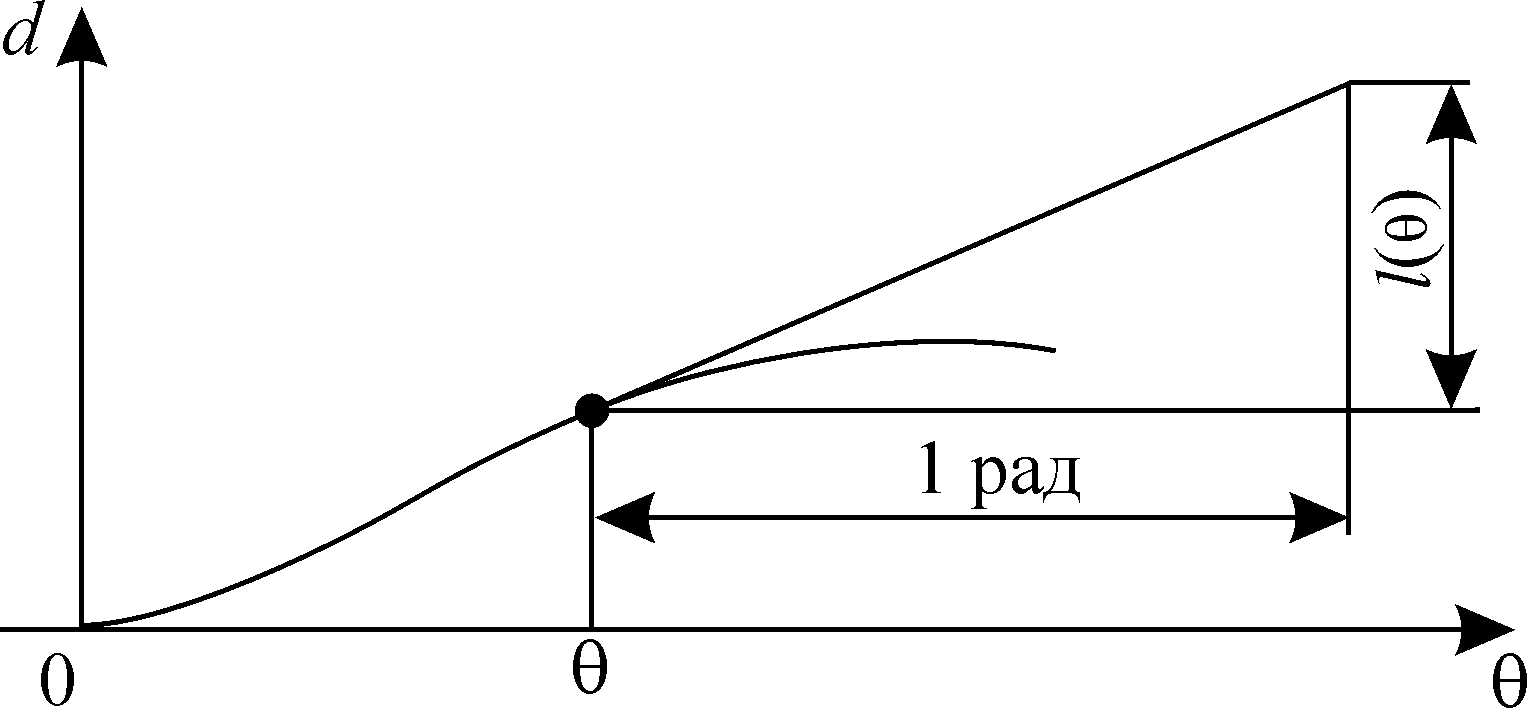
Рис.3. Определение 1(θ) по диаграмме динамической остойчивости

3.14 Изменение посадки и остойчивости судна при переносе, приеме и расходовании груза. Понятие о нейтральной плоскости.

Перенос, прием и расходование грузов являются повседневными операциями в процессе эксплуатации судна. Такие операции приводят к изменению посадки (средней осадки, углов крена и дифферента) и остойчивости судна.

1. Перенос груза

Пусть на судне некоторый груз P массой m перенесен так, что ЦТ этого груза переместился из точки с координатами x₀, y_­0, z₀ в точку с координатами x₁, y_­1, z₁. Тогда масса всего судна не изменится, но изменится положение его ЦТ. При этом рассматриваем продольное перемещение l_x = x₁ — x₀ поперечное перемещение l_y = y₁ — y₀ и вертикальное перемещение l_z = z₁ — z₀.

Перемещение ЦТ судна можно найти с помощью теоремы о статических моментах, согласно которой

; ; (7)

Благодаря этому перемещению появятся две дополнительные пары сил. Одна из них будет действовать в ДП, вызывая дифферент. Другая же будет действовать в поперечной плоскости, параллельной плоскости мидель-шпангоута, вызывая крен. равно (рис. 4).

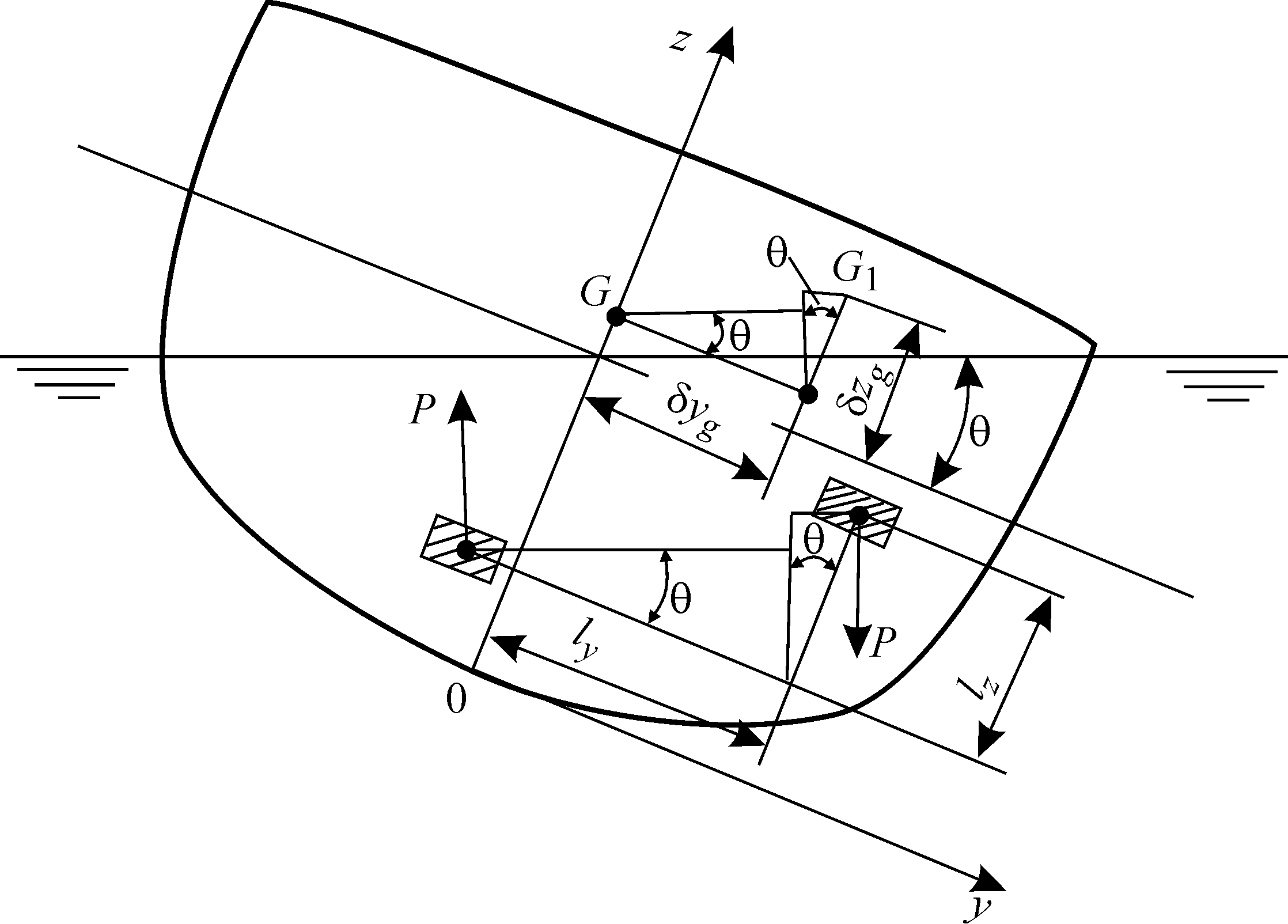
Рис. 4. Кренящая пара сил при переносе груза

Моменты этих пар равны:

(8)

Согласно условиям равновесия действие этих моментов уравновесится действием восстанавливающих моментов. Определим последние по метацентрическим формулам остойчивости :

; . (9)

Отсюда угол дифферента, возникающий вследствие переноса груза, равен

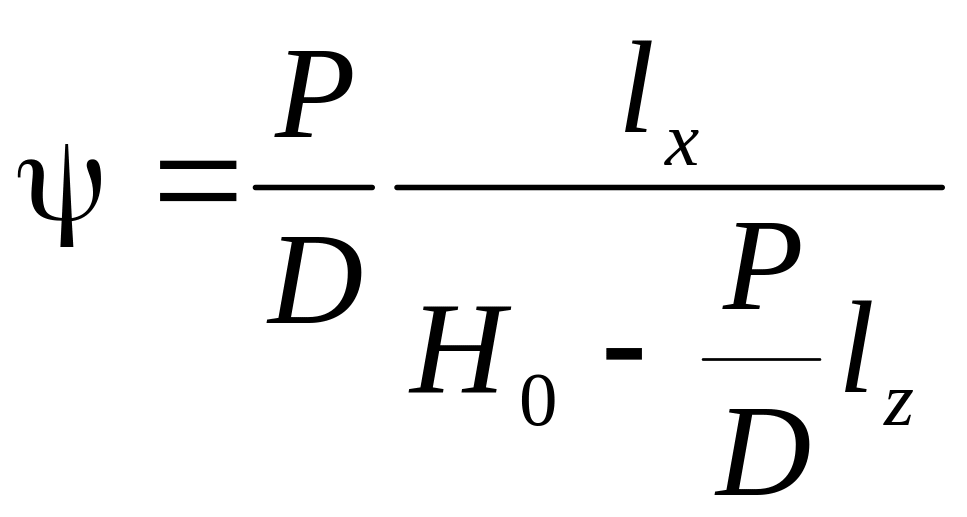, (10)

а угол крена

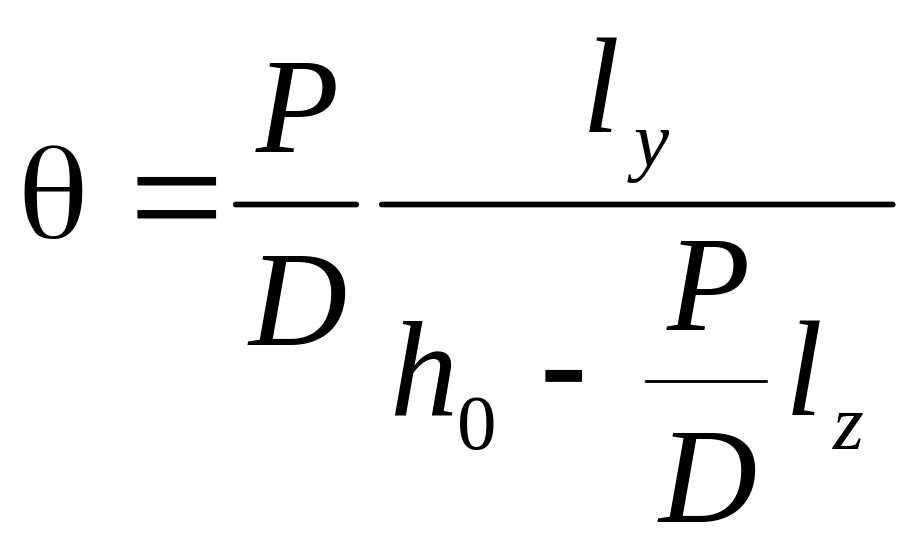. (11)

Выражения для метацентрических высот, измененные из-за влияния переноса груза, будут следующие:

; (12)

, (13)

где поправки к метацентрическим высотам оказываются одинаковыми;

. (14)

Для большинства судов продольная метацентрическая высота много больше поперечной. Поэтому в практических расчетах поправкой почти всегда можно пренебречь по сравнению с и положить . Тогда, подставив (12) и (14) в формулы (10) и (11), окончательно найдем

; (15)

Если груз переносится в нос, то , , а значит и , т. е. судно получает дифферент на нос. Если же груз переносится в корму, то , , , т. е. судно дифферентует на корму. В случае переноса груза на правый борт и , а в случае переноса на левый и .