2. Wariancja I odchylenie standardowe
Wariancją dla zbioru danych x1, x2, ..., xN dla populacji nazywamy wyrażenie:
gdzie : μ oznacza średnią dla populacji,
N – liczebność populacji.
Dla próbki o liczebności n wariancję otrzymujemy z wzoru:
gdzie
jest średnią arytmetyczną z próby.
Wzór powyższy na obliczanie wariancji przedstawia się także w następującej postaci, wygodniejszej w obliczeniach:
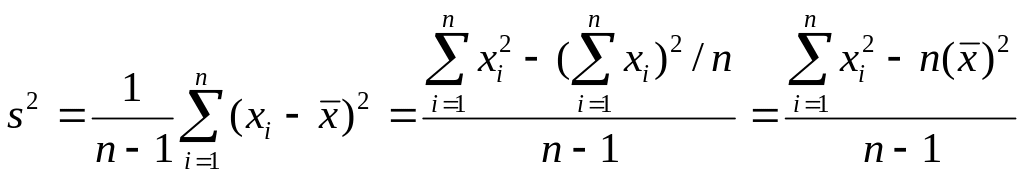
W przypadku gdy będziemy korzystać z danych pogrupowanych (szeregu rozdzielczego), odpowiednie wzory na wariancję przyjmą postać:
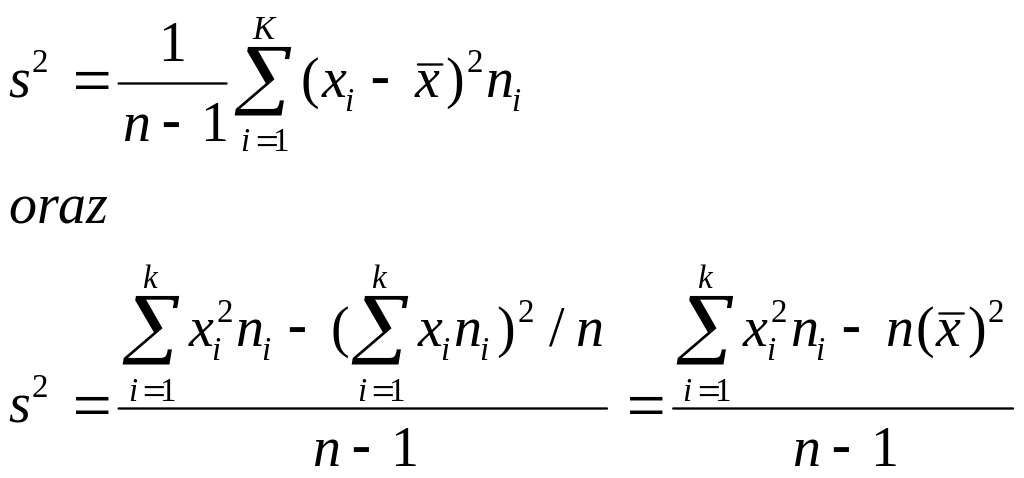
Jako miara zróżnicowana używa się też dodatniego pierwiastka kwadratowego z wariancji, który określa się mianem odchylenia standardowego:
Odchylenie standardowe ma takie samo miano jak badana cecha, a jego własności wywodzą się bezpośrednio z własności wariancji.
3. Współczynnik zmienności
Współczynnik zmienności to iloraz odchylenia standardowego i średniej w danym rozkładzie:
Współczynnik zmienności wyraża się często procentowo: V x 100%, aby określić, jaki procent poziomu średniej stanowi odchylenie standardowe w rozkładzie. Im wyższy jest ten procent, tym większe jest zróżnicowanie tym cecha jest bardziej zróżnicowana..
Przykład IV.
W przedsiębiorstwie produkcyjnym kontrola jakości wykryła u dwóch robotników następującą liczbę braków w 9 partiach liczących po 100 elementów:
Nr partii |
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
Robot. A |
3 |
4 |
2 |
4 |
1 |
2 |
3 |
2 |
5 |
Robot. B |
5 |
3 |
8 |
4 |
2 |
3 |
4 |
6 |
3 |
Obliczyć, który z robotników nie spełnił warunków jakości przyjęcia wyprodukowanych partii produktów, jeśli odbiorca towarów przyjął, aby mediana liczby braków nie była większa niż 3,5 , średnia nie większa niż 4, a zmienność nie przekraczała 45%.
Rozwiązanie:
Obliczamy najpierw średnie arytmetyczne braków dla robotników: A i B, z wzoru:
,
tj.
Obliczamy mediany dla robotników A i B:
a) porządkujemy wartości braków robotnika A według wielkości: 1, 2, 2, 2, 3, 3, 4, 4, 5. Wartość środkowa wyznacza medianę dla robotnika A, tj. MA = 3;
b) porządkujemy wartości braków robotnika B według wielkości: 2, 3, 3, 3, 4, 4, 5, 6, 8.
Wartość środkowa wyznacza medianę dla robotnika A, tj. MA = 4.
Obliczamy wariancję braków dla poszczególnych robotników wg wzoru:
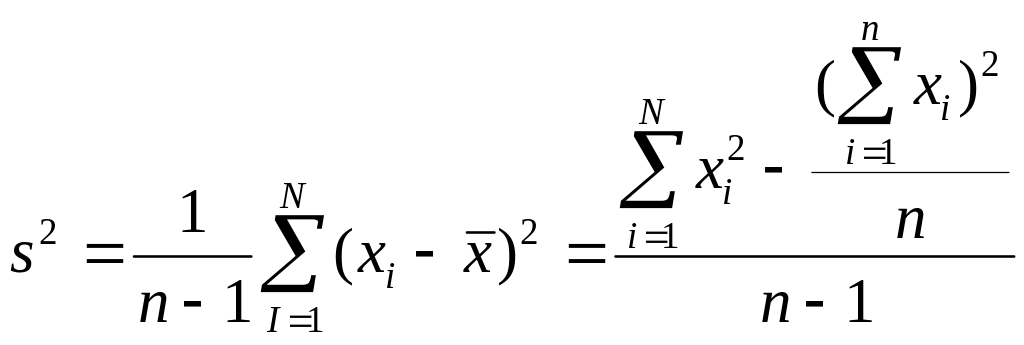Korzystamy z drugiej części wzoru
Otrzymujemy: dla robotnika A i B:
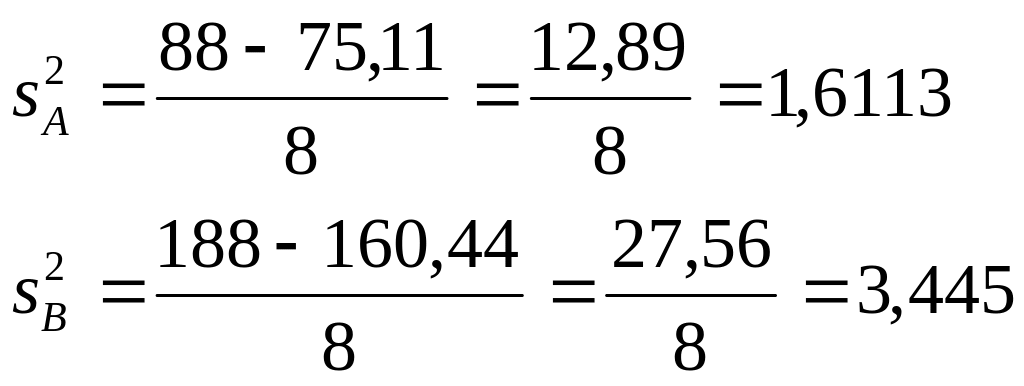
Obliczamy odchylenie standardowe braków:
dla robotnika A: sA=0,782;
dla robotnika B: sA=1,856;
Obliczamy współczynniki zmienności wg wzoru:
;
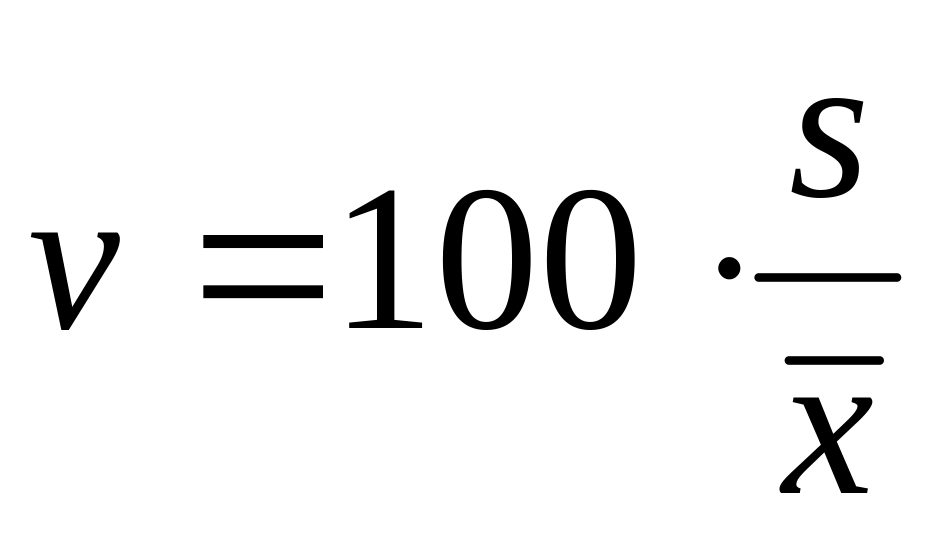vA=27,1%; vB=79,6%;
Odpowiedź: Robotnik B nie spełnił żadnego warunku jakości produktu.
Asymetria I koncentracja
6.1. Asymetria I jej miary
6.2. Koncentracja I jej mierzenie