Podstawowe rozkłady zmiennych losowych

Podane niżej rozkłady teoretyczne zmiennej losowej będą wykorzystane w dalszych wykładach:

1. rozkład normalny (tablice)

2. rozkład t-Studenta (tablice)

3. rozkład binominalny

1. Rozkład normalny

.

Rozkład normalny, najczęściej używany i odgrywający ważną rolę w statystyce, został wyprowadzony po raz pierwszy w 1733 r. przez A. de Moivre'a jako graniczna forma rozkładu dwumianowego. Ponownie rozkład ten został odkryty przez A. Laplace'a (1812) i C. F. Gaussa (1809) i stał się znany jako normalny lub gaussowski rozkład błędów. Przez wiele lat sądzono, że rozkład normalny najczęściej występuje w rzeczywistości, stąd jego nazwa normalny. Obecnie wiadomo, że jest to jeden z możliwych rozkładów i niewiele zjawisk ekonomicznych i społecznych można opisać przy pomocy tego rozkładu, jednakże znaczenie jego w statystyce, co zresztą zobaczymy dalej, jest bardzo duże.

Pomimo, że prawie każdy statystyk miał wiele okazji spotkać się z rozkładem normalnym, to jednak warto tu przypomnieć niektóre informacje, które będą potrzebne w dalszych rozważaniach. Rozkład normalny dotyczy ciągłych zmiennych losowych, a jego funkcja gęstości wyraża się przy pomocy następującego wzoru:

gdzie: m - wartość oczekiwana zmiennej (średnia),

s - odchylenie standardowe zmiennej,

exp(z) = e^z, gdzie e jest podstawą logarytmów naturalnych (e = 2,71828...).

W praktyce często wykorzystuje się dystrybuantę rozkładu normalnego, która przyjmuje postać:

widzimy więc, że rozkład normalny zależy od dwóch parametrów: µ tj. wartości oczekiwanej (średniej) zmiennej losowej X oraz σ - odchylenia standardowego (zwane jest również odchyleniem średnim). Rozkład normalny o wartości oczekiwanej µ i odchyleniu standardowym σ oznacza się przez .

Rys. 1. Wartość dystrybuanty rozkładu normalnego Φ(u₁) dla kwantyla u₁

Standaryzacja rozkładu normalnego

W praktyce bardzo ważne znaczenie odgrywa standaryzowany rozkład normalny, tj. taki rozkład normalny, w którym m = 0 oraz s = 1. Standaryzacja rozkładu normalnego polega na odjęciu od zmiennej X wartości średniej m i podzieleniu przez odchylenie standardowe , tzn. jeśli zmienna losowa ma rozkład normalny, to zmienna standaryzowana ma rozkład N(0, 1). Standaryzację rozkładu normalnego przeprowadza się w tym celu, aby można było obliczyć wartości dystrybuanty (lub funkcji gęstości) ze specjalnych tablic statystycznych. Dystrybuantę standaryzowanej zmiennej losowej normalnej oznacza się zwykle przez F(u) (rys. 1), a gęstość przez y(u).

Warto jeszcze zwrócić uwagę na następujące związki, z których często korzysta się w praktyce

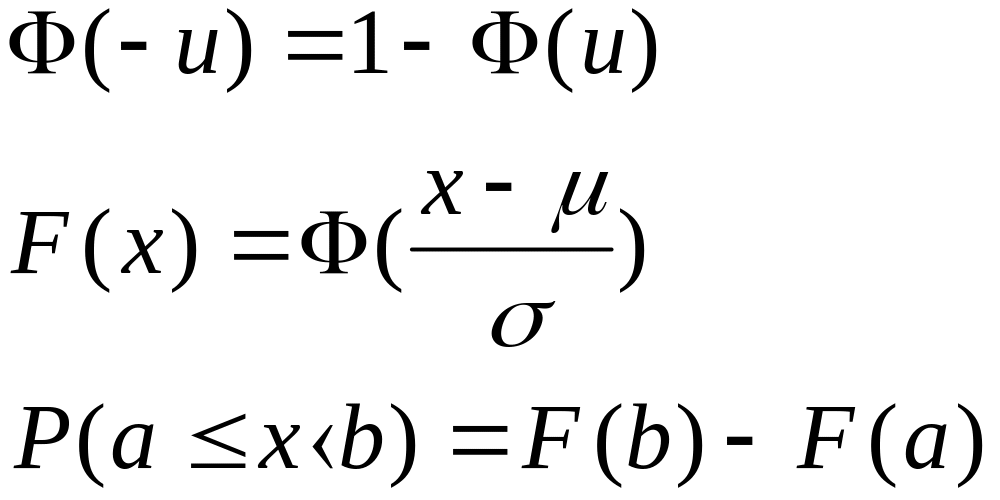
Niezbędne będzie jeszcze pojęcie kwantyla rzędu p zmiennej N(0,1) oraz zmiennej N(m, s), a także wykazanie zależności między tymi kwantylami (rys. 2).

Rys. 2. Kwantyle rozkładu normalnego

Kwantylem rzędu p zmiennej losowej U (tj. zmiennej losowej standaryzowanej) nazywamy taką liczbę, że

Między kwantylami zmiennej losowej U zachodzi następujący związek:

Znając kwantyl rzędu p zmiennej losowej U, tj. u_p można obliczyć kwantyl rzędu p zmiennej losowej X o rozkładzie z następu­jącej zależności:

.

Ponieważ wartość dystrybuanty (lub funkcji gęstości) standa­ryzowanego rozkładu normalnego, tj. wartości F(u) (lub y(u)), publikowane są w specjalnych tablicach statystycznych (por. R Zieliński: Tablice statystyczne, PWN, Warszawa 1972, s 106 i wydania późniejsze), a nawet zamieszczane są prawie w każdym podręczniku rachunku prawdopodobieństwa i statysty­ki matematycznej, więc wartości dystrybuanty zmiennej losowej można szybko odczytać z tablic, po przeprowadzeniu standaryzacji zmiennej X. Umożliwia to obliczenie także innych zależności między charakterystykami zmiennej N(m, s) oraz zmiennej N(0,1), co jak, zobaczymy dalej, ma bardzo ważne znaczenie w statystyce, a szczególnie w zastosowaniach metody reprezentacyjnej oraz wnioskowaniu statystycznym.

Przykład I. Wydajność pracy w fabryce jest zmienną losową o rozkładzie normalnym z wartością oczekiwaną 12 ton/godz. (m = 12) i odchyleniem standardowym 2 tony/godz. (s = 2), tj. N (12; 2). Obliczyć prawdopodobieństwo, że wydajność pracy jest:

a) mniejsza niż 15 ton/godz,

b) jest zawarta w przedziale od 8 do 16 ton/godz,

c) większa niż 19 ton/godz.

Rozwiązanie:

1. Zapisujemy punkt a) w zapisie prawdopodobieństwa i standaryzujemy, aby skorzystać z tablic rozkładu normalnego i znaleźć szukane prawdopodobieństwo: . Prawdopodobieństwo to wynosi więc 0,9332.

2. Punkt b) zapisujemy w wyrażeniach prawdopodobieństwa, standaryzujemy oraz znajdujemy odpowiednie wartości w tablicach rozkładu normalnego: . Skorzystaliśmy tu z faktu, że a dla x = -2 mamy . Szukane prawdopodobieństwo wynosi: 0,9545.

3. Podobnie, jak w poprzednich punktach zapisujemy w wyrażeniach prawdopodobieństwa i korzystamy z warunku, że 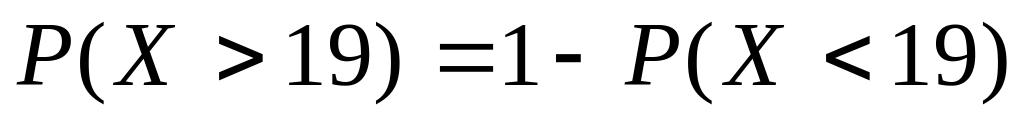, stąd otrzymamy: Szukane prawdopodobieństwo wynosi: 0,00023.

Rozkład dwumianowy (binominalny), schemat Bernoulliego

Zmienna losowa o rozkładzie dwumianowym określana jest w tzw. schemacie Bernoulliego. Rozpatruje się doświadczenie, którego rezultatem może być zdarzenie A (sukces) lub zdarzenie przeciwne A’ (porażka). Prawdopodobieństwo sukcesu w pojedynczym doświadczeniu wynosi p, a porażki 1-p. Doświadczenie powyższe powtarza się niezależnie,

tzn. przy zachowaniu stałego prawdopodobieństwa sukcesu, n razy. Zmienną losową definiujemy jako liczbę uzyskanych sukcesów, tzn. . Jest widoczne, że zmienna losowa X jest typu skokowego i przyjmuje wartości k = 1, 2, …, n. Prawdopodobieństwo tego, że zmienna losowa X przyjmie wartość k (k = 1, 2, …, n.) wyraża się wzorem:

(1)

gdzie jest liczbą kombinacji k-elementowych ze zbioru n-elementowego.

Rozkład zmiennej losowej określony funkcją prawdopodobieństwa wyrażającą się powyższym wzorem jest rozkładem dwumianowym z parametrami n i p. Wartość oczekiwana i odchylenie standardowe wynoszą odpowiednio : E(X) = np oraz .