Задача 5

РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ

Условие задачи

Для плоской стальной рамы задана нагрузка. Схемы рам приведены в таблице 5.1, исходные значения указаны в таблице 5.2.

требуется подобрать двутавровое сечение рамы.

Краткие теоретические сведения

В данной задаче рассматриваем плоскую раму, имеющую одну важную особенность: количество опорных связей превышает количество уравнений статического равновесия рамы (т. е. уравнений статики).

Как известно, для геометрической неизменяемости плоской рамы требуются три опорные связи. Рама может иметь либо одно жёсткое защемление, либо три шарнирные опирания, где возникают три опорные реакции, величины которых можно найти из уравнений статического равновесия (уравнений статики). Поэтому раму с тремя опорными связями называют статически определимой.

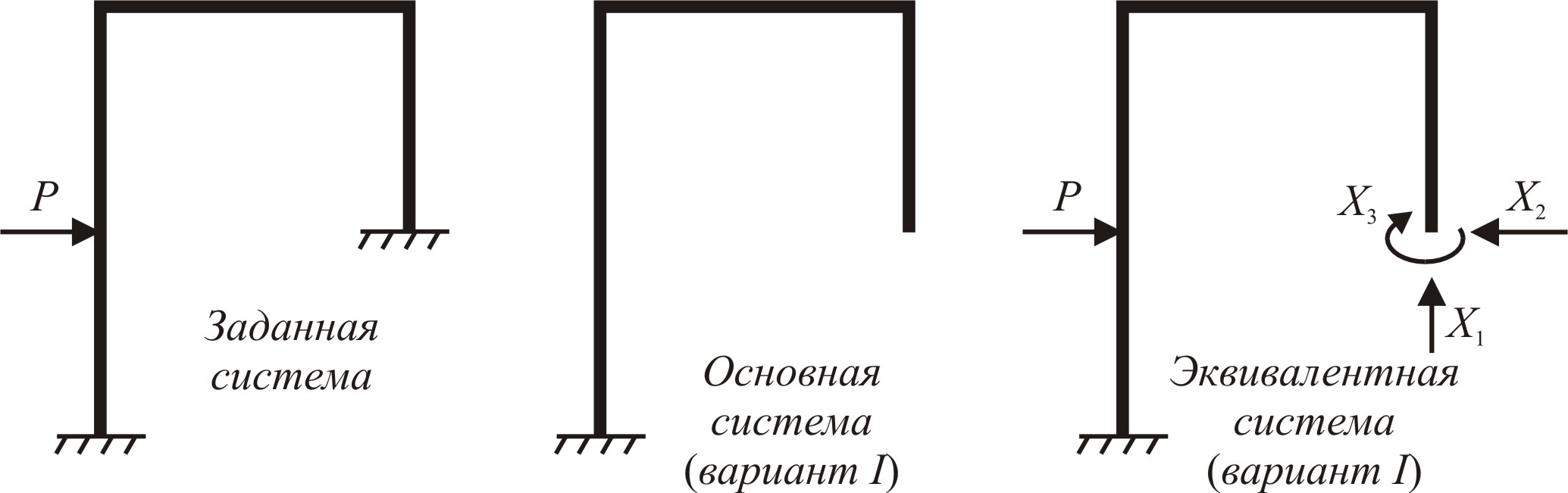
Если рама не имеет достаточной жёсткости, то приходится вводить дополнительные опоры (т. е. дополнительные связи), позволяющие достичь необходимой жёсткости. Так, рама на рис. 7.1, а имеет одно дополнительное жёсткое защемление, значит, имеет три дополнительные связи (три дополнительные опорные реакции). В раме с дополнительными связями значения всех реакций уже невозможно найти по уравнениям статики, поэтому она называется статически неопределимой. Расчёт плоской статически неопределимой рамы и выполняется в данной задаче.

Количество дополнительных связей есть степень статической неопределимости, обозначим её буквой С. Дополнительные связи часто называют «лишними» (с точки зрения статики). Нахождение величин «лишних» связей называют раскрытием статической неопределимости. Это первый пункт расчёта статически неопределимой рамы.

Для раскрытия статической неопределимости рам составляют столько дополнительных уравнений, сколько имеется дополнительных опорных связей. Для получения дополнительных уравнений используют наряду с другими метод сил, согласно которому удаляют все «лишние» связи и вместо них ставят неизвестные усилия X₁, X₂, …, X_с (среди них могут быть и силы, и моменты).

При использовании метода сил сначала нужно найти степень статической неопределимости С. Здесь можно пользоваться простой формулой

С = К_R – 3, (5.1)

где К_R – количество опорных связей в заданной раме; 3 – количество уравнений статического равновесия плоской рамы. Но заметим, что если рама имеет замкнутые контуры или встроенные шарниры, степень статической неопределимости вычисляется по другой формуле.

Удаляя «лишние» связи, превращаем заданную раму в статически определимую, которую принято называть основной системой (рис. 5.1, б). При выборе основной системы нужно помнить о том, что в соответствии с общими требованиями механики основная система не должна быть мгновенно изменяемой. Приложив к основной системе заданную внешнюю нагрузку и неизвестные усилия X₁, X₂, …, X_с отброшенных связей, получаем эквивалентную систему, в которой перемещения и напряжения такие же, как в заданной, а значит, она эквивалентна заданной (рис. 5.1, в).

а б в

Рис. 5.1

Далее составляют дополнительные уравнения, которые являются каноническими уравнениями метода сил: для n раз статически неопределимых систем они имеют вид

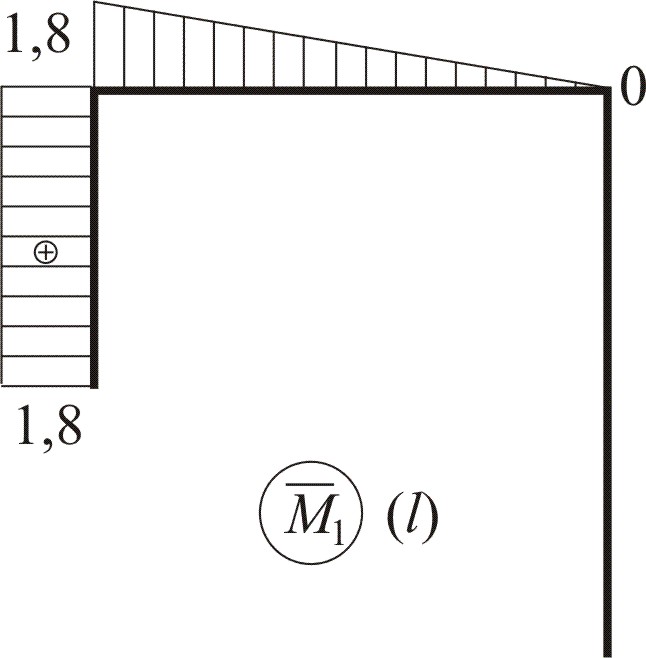
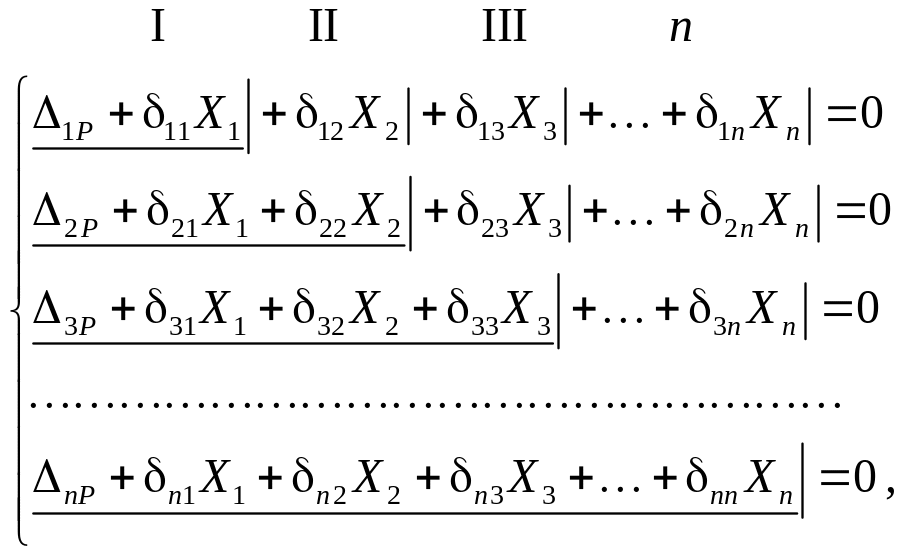(5.2)

где чертой и индексом I показано уравнение для решения один раз статически неопределимой системы, чертой и индексом II – уравнения для решения дважды неопределимой системы и т. д. Коэффициенты δ₁₁, ₁₂, …, δ_nn представляют собой единичные перемещения, это перемещения от действия единичных сил в основной системе. Свободные члены _1P, _2P, …, _nP есть грузовые перемещения ̶ перемещения в основной системе от внешней нагрузки. Вычисления перемещений в рамах производят методом Мора или способом Верещагина. Здесь при расчёте рам использован способ Верещагина.

Необходимо понимать физический смысл канонических уравнений (5.2) метода сил: каждое уравнение записывает равенство нулю перемещения на каждой дополнительной опоре, поэтому в левой части уравнений для учёта заданной внешней нагрузки и неизвестных усилий X₁, X₂, …, X_с отброшенных связей стоит сумма перемещений от внешней нагрузки и от каждого дополнительного усилия X₁, X₂, …, X_n.

Решив систему уравнений (5.2), получим значения усилий X₁, X₂, …, X_n, и таким образом раскроем статическую неопределимость рамы. Укажем последовательность пунктов в раскрытии неопределимости:

1. Выбор основной системы.

2. Построение эпюр грузовых и единичных моментов.

3. Перемножение эпюр и решение канонических уравнений.

Затем производят необходимые расчёты на прочность и жёсткость.

Решение задачи 5

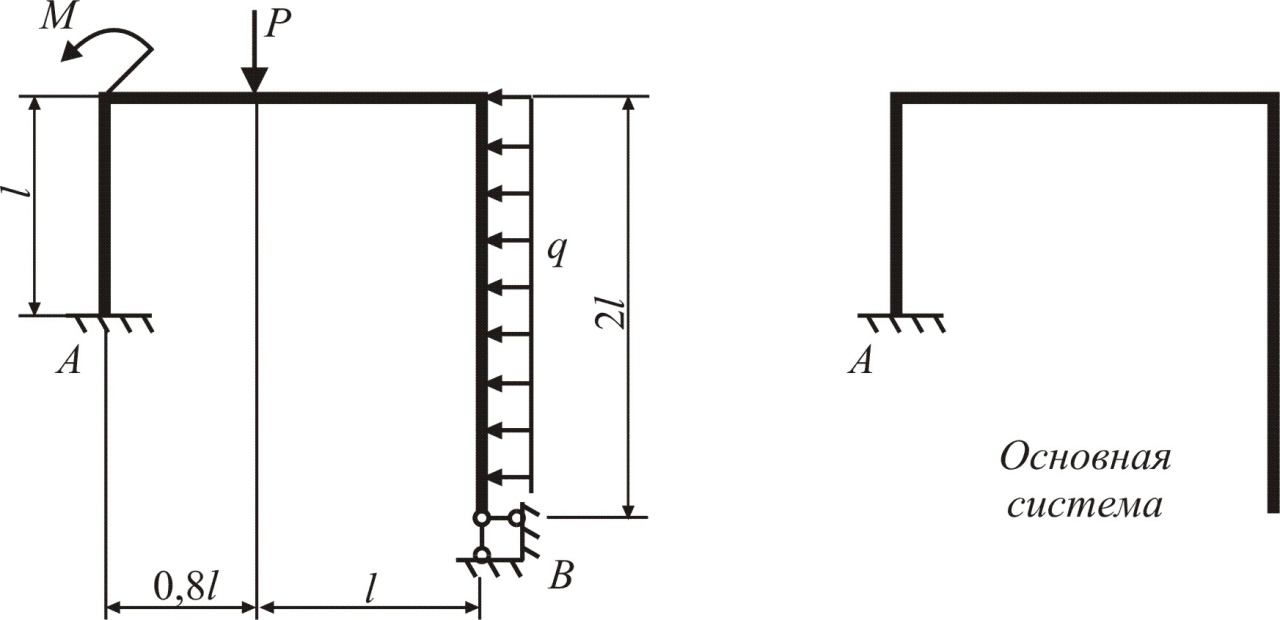
Подобрать двутавровое сечение плоской рамы (рис. 5.2, а) при следующих значениях: М = 1,7ql², P = 1,2ql, q = 32 кн/м, l = 1,2 м.

1. Выбор основной системы

Для определения степени статической неопределимости подсчитаем количество реакций в раме: в заделке А имеем три реакции и в шарнирно-неподвижной опоре В – две, итого пять реакций. Тогда по формуле (5.1)

С = К_R – 3= 5 – 3 = 2.

Значит, система дважды статически неопределимая, имеет две лишние связи.

Освобождаем раму от двух связей таким образом, чтобы получить статически определимую, геометрически неизменяемую раму – основную систему. Из схемы рамы видно, что за «лишние» неизвестные удобнее всего принять опорные реакции Х₁ и Х₂ в шарнире В (рис. 5.2, в).

При наложении на основную систему всех внешних нагрузок и неизвестных сил Х₁ и Х₂ получается статически эквивалентная система (рис. 5.2, в). Так как рассматриваемая рама дважды неопределима, то канонические уравнения метода сил (5.2) принимают вид:

(5.3)

а		б
в		г
д		е

Рис. 5.2

Для вычисления коэффициентов канонических уравнений ₁₁, ₁₂ = ₂₁, ₂₂, _1Р, _2Р необходимо предварительно построить эпюры моментов от внешних нагрузок (эпюру грузовых моментов М_Р) и от единичных сил  = 1 и  = 1 (эпюры единичных моментов и ).

2. Построение эпюр грузовых и единичных моментов

Запишем грузовые моменты по участкам, используя эквивалентную систему (рис. 5.2, в) и учитывая в записи только внешнюю нагрузку. Напомним правило знаков момента: если наблюдатель, помещённый внутрь рамы, видит растянутые волокна стержня на каком-то участке, то на этом участке изгибающий момент положительный; если он видит сжатые волокна, то изгибающий момент отрицателен.

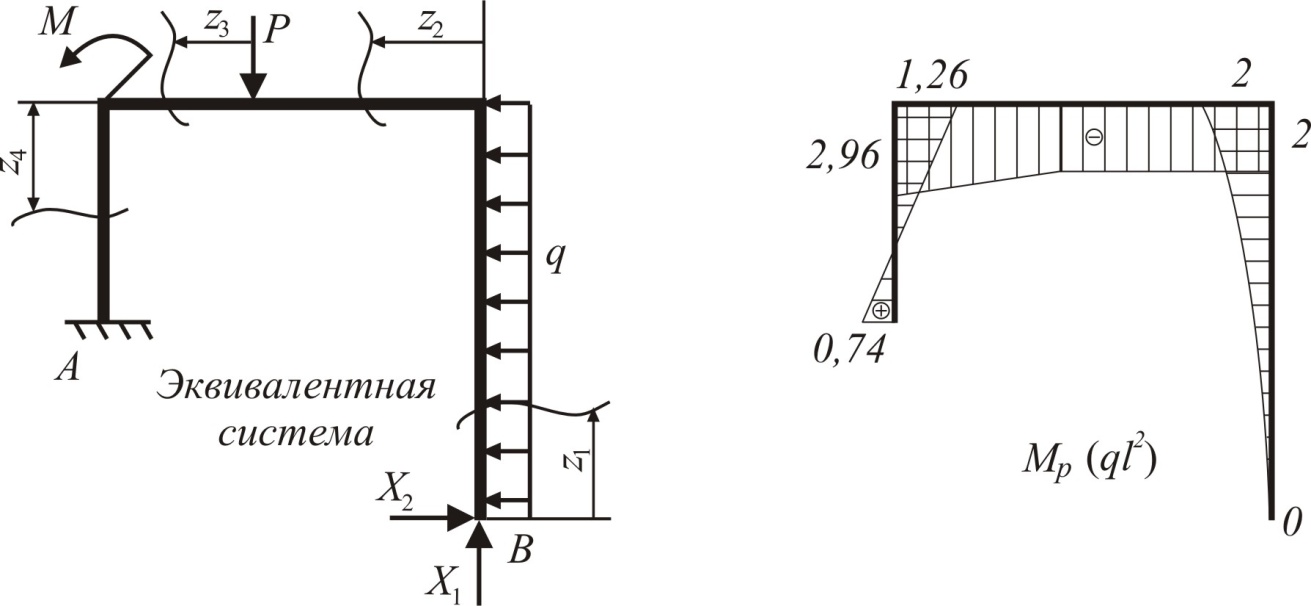
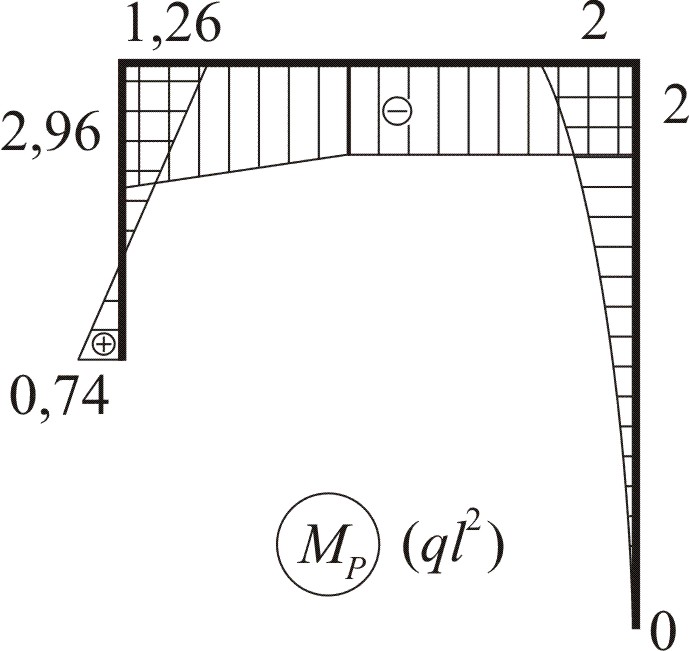
Разобьём эквивалентную систему на характерные участки (их четыре) и покажем текущие координаты z_i. Получаем

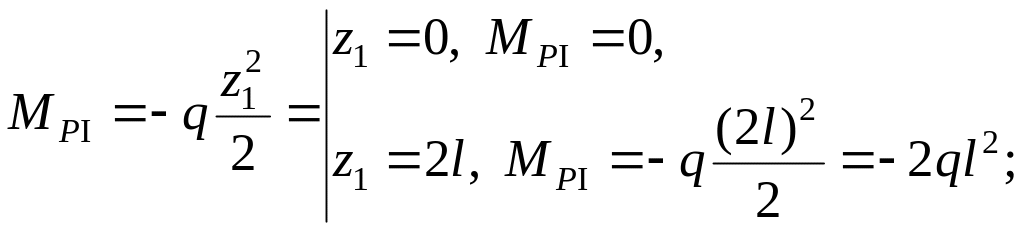
M_PII = –q2l · l = –2ql²;

По этим значениям построим эпюру грузовых моментов M_P (рис. 5.2, г).

Используя также эквивалентную систему (рис. 5.2, в) и те же текущие координаты z_i, найдём единичные моменты и от единичных сил = 1 и = 1:

По этим значениям построены эпюры единичных моментов и на рис. 5.2, д, е.

3. Перемножение эпюр и решение канонических уравнений

Коэффициенты уравнения (5.3) находим способом Верещагина: для единичных коэффициентов перемножаем эпюры единичных моментов и по формуле для грузовых коэффициентов _1Р и _2Р перемножаем эпюры единичных моментов и на эпюру грузовых по формуле

Для перемножения можно использовать формулы табл. П.7 Приложения. В нашем случае, вычисляя площадь фигуры одной эпюры и значения моментов под её центром тяжести из другой соответствующей эпюры, получаем значения коэффициентов:

Подставим найденные коэффициенты в канонические уравнения (5.3):

Упростим уравнения, сократив их на l³ и жёсткость EJ:

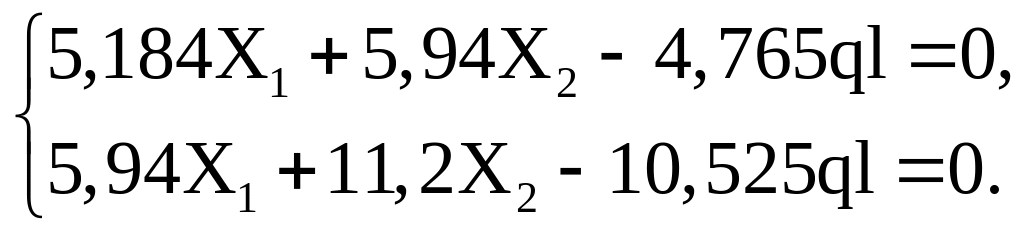
Выразим из первого уравнения X₁ через X₂:

X₁ = (–5,94X₂ + 4,765ql) = –1,146X₂ + 0,919ql

и подставим получившееся выражение во второе уравнение и найдём значение X₂:

5,94(–1,146X₂ + 0,919ql) + 11,2X₂ –10,525ql = 0,

–6,807X₂ + 5,46ql + 11,2X₂ –10,525ql = 0,

4,393X₂ –5,065ql = 0,

X₂ = = 1,153ql.

Тогда X₁ = –1,146 · 1,153ql + 0,919ql = –0,402ql.