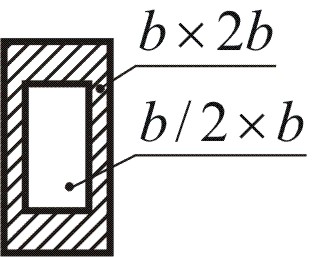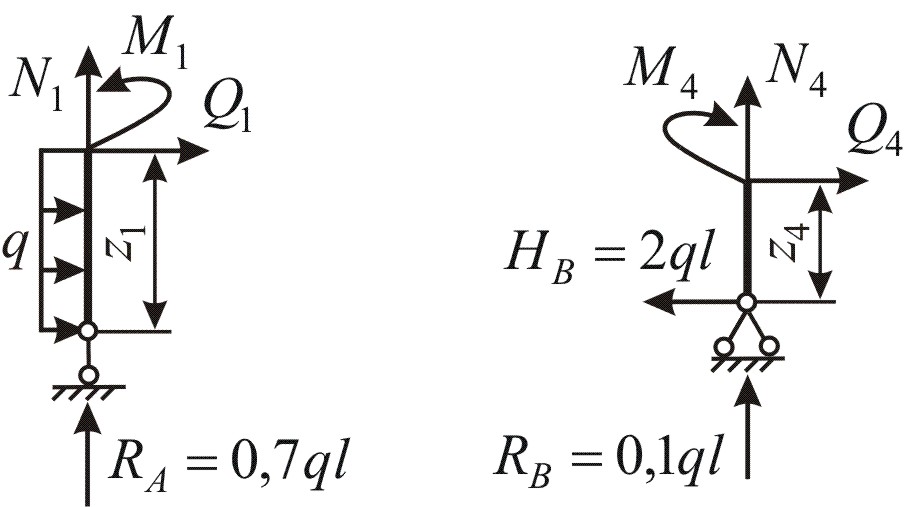Задача 4

Расчёт плоской рамы

Условие задачи

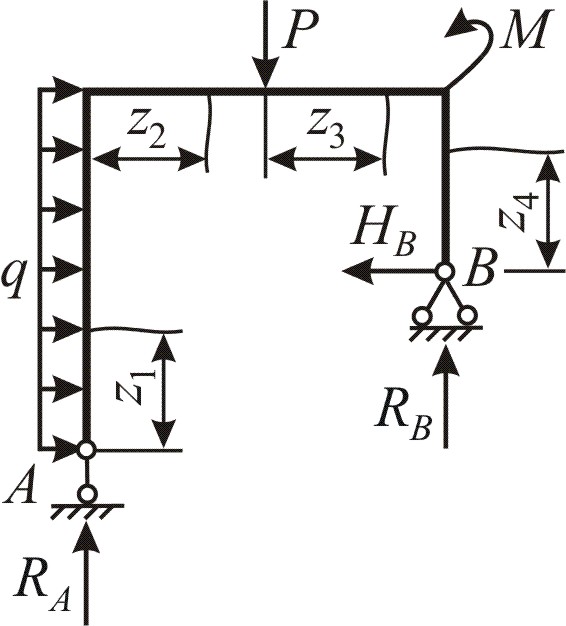
Для плоской стальной рамы известна нагрузка: рама нагружена распределённой нагрузкой, сосредоточенной силой и моментом. Схемы приведены рамы в таблице 4.1. Числовые значения и вид сечения указаны в таблице 4.2.

требуется: 1. Подобрать размеры поперечного сечения.

2. Вычислить горизонтальное, вертикальное и угловое перемещения сечения .

Краткие теоретические основы решения

Рамой называют конструкцию, которая состоит из жёстко соединённых стержней (рис. 5.1, а). Чаще соединение выполняют под прямым углом, и размеры сечения всех стержней одинаковы. Стержни могут быть прямолинейными и криволинейными. Здесь рассмотрим расчёт плоской рамы с прямолинейными стержнями. Для расчёта составляют расчётную схему плоской рамы – это геометрический контур реальной рамной конструкции, на котором каждый стержень изображается в виде прямого бруса, показана последовательность соединения стержней и внешняя нагрузка.

Каждый стержень может быть нагружен распределённой нагрузкой, сосредоточенными силами и моментами. Если эта нагрузка лежит в плоскости рамы, то имеем плоскую раму. В своей плоскости такая рама должна иметь опоры (это опирание или соединение с другими конструкциями). На расчётной схеме изображают заделку, если опора препятствует как линейным, так и угловым перемещениям. Когда реальная опора препятствует только одному перемещению, то на схеме ставят шарнирно-подвижную опору. В случае опоры, препятствующей двум линейным перемещениям в плоскости рамы, на расчётной схеме изображают шарнирно-неподвижную опору. В опорах возникают опорные реакции. В заделке – вертикальная и горизонтальная силы и изгибающий момент; в шарнирно-подвижной опоре одна сила; в шарнирно-неподвижной – две взаимно перпендикулярные силы. Причём число опорных реакций не должно быть менее трёх, иначе рама станет геометрически изменяемой, т. е. рама получит смещения и не будет уравновешенной системой. Так, рама, изображённая на рис. 4.1, а, имеет шарнирно-подвижную и шарнирно-неподвижную опоры, общее количество опорных реакций равно трём, и рама геометрически неизменяемая.

Значения опорных реакций необходимы для решения задачи. Опорные реакции и внешние воздействия располагаются в плоскости рамы и создают плоскую систему сил, поэтому для вычисления опорных реакций составляем три уравнения равновесия:

(4.1)

оставляя неиспользованное уравнение для проверки реакций.

Как известно, для расчётов на прочность и жёсткость необходимо знать внутренние усилия, которые определяются известным методом сечений по правилу РОЗУ: Разрезать, Отбросить, Заменить, Уравновесить. Необходимо выполнить разрез в текущем сечении рамы, рассмотреть отсечённые части и составить уравнения равновесия отсечённой части по уравнениям равновесия в виде:

(4.2)

А		б
В	г

Рис. 4.1

Как показывают условия равновесия отсечённых частей (рис. 4.1, б, г), равновесие соблюдается, если в сечении возникают продольная сила N, поперечная сила Q и изгибающий момент M строго определённого значения и направления. Таким образом, в поперечных сечениях плоской рамы возникают три вида внутренних усилий: продольная сила, поперечная сила и изгибающий момент. Поэтому для плоских рам строят три эпюры – эпюры N, Q, M. Это весьма трудоёмкий пункт расчёта рам. Чтобы успешно выполнить построение эпюр, нужно помнить принципы построения эпюр продольных сил N при растяжении-сжатии, эпюр поперечных сил Q и изгибающих моментов M при плоском изгибе балок.

Так как в сечениях плоских рам возникают одновременно продольные силы , поперечные силы Q и изгибающие моменты M = M_x, то наблюдается сложное сопротивление: совокупность осевого растяжения-сжатия и плоского изгиба. Тогда нормальные напряжения σ определяются суммой напряжений от осевого растяжения-сжатия и плоского изгиба; и касательные напряжения τ, возникают от поперечной силы. Эти напряжения вычисляют по формулам

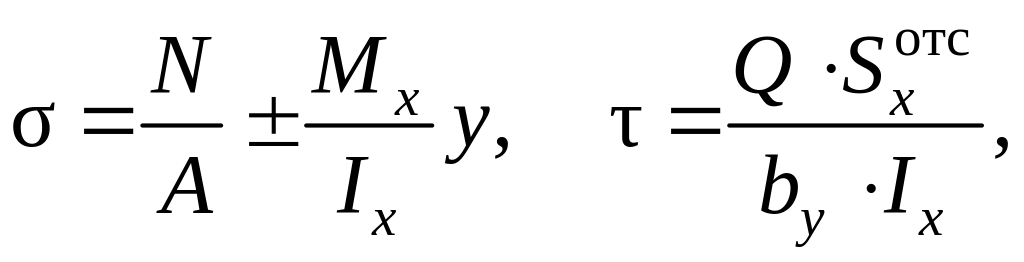
где А – площадь сечения, I_x – осевой момент инерции сечения; – статический момент инерции отсеченной части сечения; b_y – ширина слоя сечения.

Но слагаемое N/А часто составляет малую часть от всего нормального напряжения σ. Рассуждая с этой точки зрения, иногда говорят, что стержни плоской рамы работают в основном на изгиб. При выполнении проектного расчёта плоских рам, чтобы не усложнять подбор размеров сечения, размеры определяют из условия прочности по нормальным напряжениям изгиба

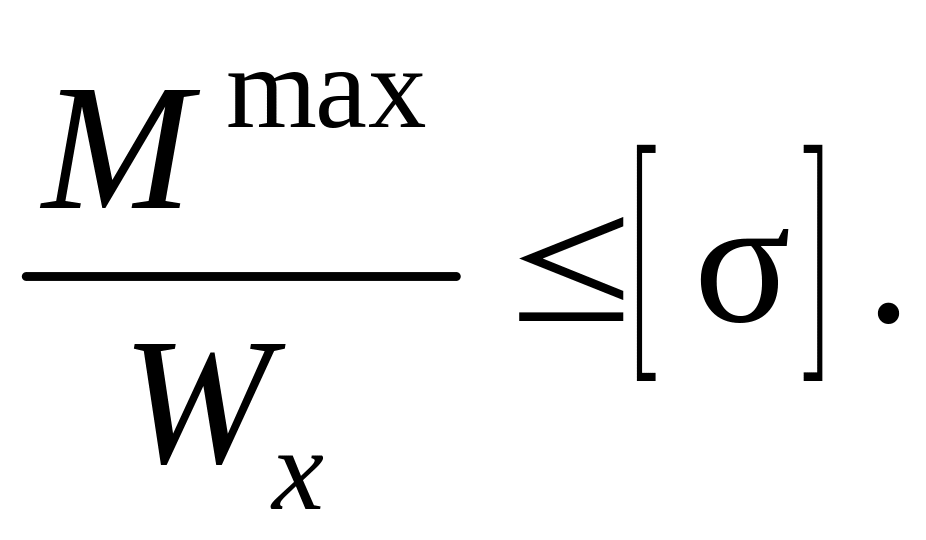(4.3)

Условие (4.3) составляют для опасного сечения рамы, которое нужно установить по эпюре изгибающих моментов M.

После подбора сечения выполняют проверку прочности с учётом сложного сопротивления. Эту проверку начинают с вычисления записанных выше нормальных σ и касательных напряжений τ, потом выявляют опасное сечение и опасную точку этого сечения, вид напряжённого состояния в опасной точке, выбирают и проверяют необходимое условие прочности для сложного сопротивления.

Возможны следующие условия прочности:

1. В случае совместного изгиба и продольной силы в опасном сечении условие прочности имеет вид

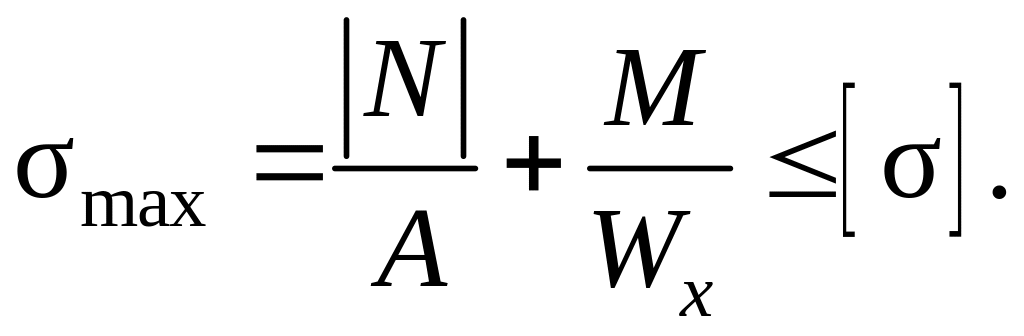(4.4)

Здесь нужно помнить, что условие (4.4) используется при отсутствии касательных напряжений или при их малом значении.

2. При совместном наличии в опасной точке сечения нормальных и касательных напряжений, соизмеримых по величине, условие прочности записываем по теориям прочности. Например, по III теории прочности

(4.5)

Пример решения задачи 4

Дано l = 2 м, q = 12 кН/м, отношения P/q = 0,8; M/ql² = 0,6; форма сечения – коробчатое сечение b  h при соотношении всех сторон 2 (рис. 4.1, а, в).

1. Построение эпюр продольных сил, поперечных сил и изгибаю-щих моментов

Определим опорные реакции, составив уравнения (4.1)

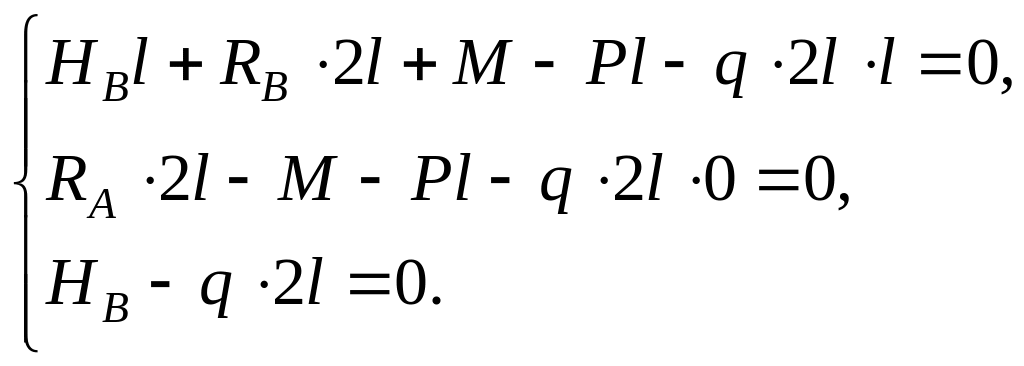
Получаем

Проверим реакции неиспользованным уравнением ∑пр y ≡ 0:

Для построения эпюр продольных сил N, поперечных сил Q и изгибающих моментов M используем метод сечений. Разделяем раму на грузовые участки. В рамах границами участков являются также узлы. Поэтому имеем четыре силовых участка. Абсциссы z текущих сечений для всех участков показаны на рис. 4.1, б. Правила знаков продольных сил N, поперечных сил Q и изгибающих моментов M такие, как при растяжении-сжатии и при плоском изгибе балок.

Рассматривая равновесие отсечённой части, наблюдатель находится внутри рамы лицом к стержню.

1-й участок: 0 ≤ z₁ ≥ 2l. Составляя уравнения (4.2) для отсечённой части 1-го участка, изображённой на рис. 4.1, г, получаем

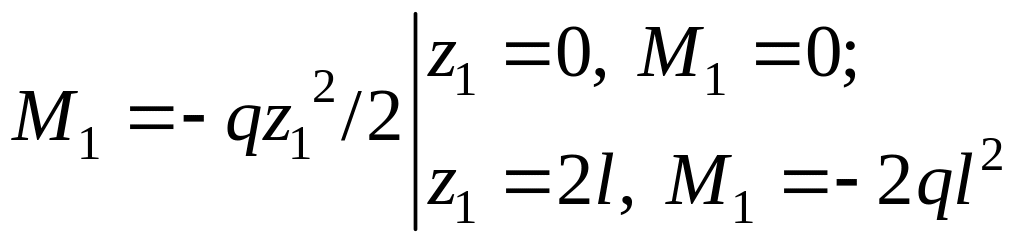, сжатые волокна справа;

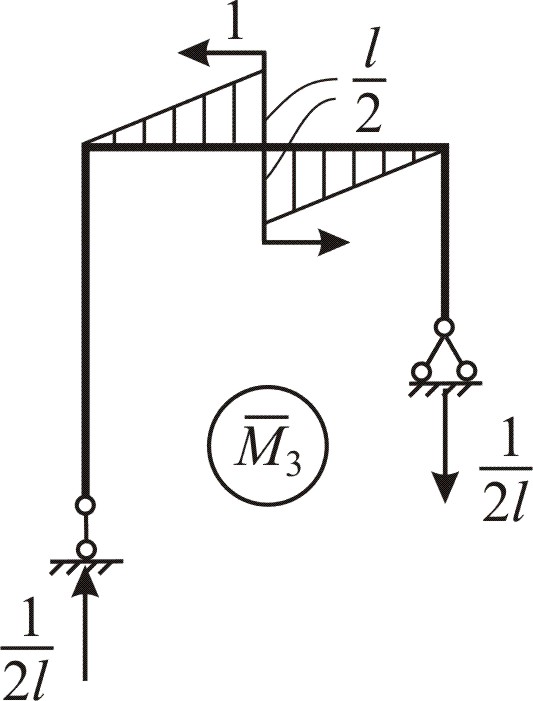
2-й участок: 0 ≤ z₂ ≥ (см. рис. 5.1, б).

сжатые волокна снизу;

А	б
В	г
д	е

Рис. 4.2

3-й участок: 0 ≤ z₃ ≥ l (см. рис. 4.1, б).

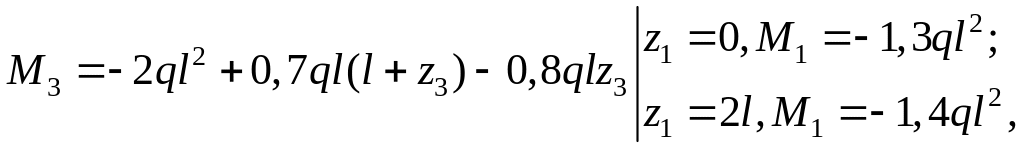- сжатые волокна снизу.

4-й участок: 0 ≤ z₄ ≥ l. Начало координаты z₄ для удобства выбираем на опоре В. Для отсечённой части 4-го участка, изображённой на рис. 4.1, г, получаем

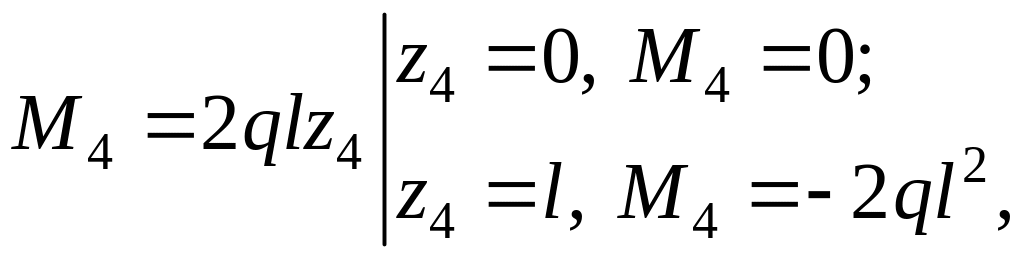сжатые волокна справа.

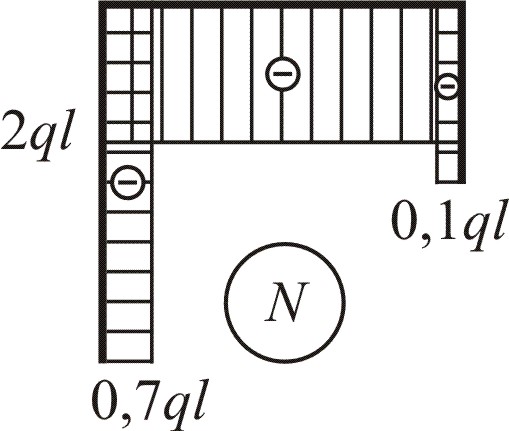
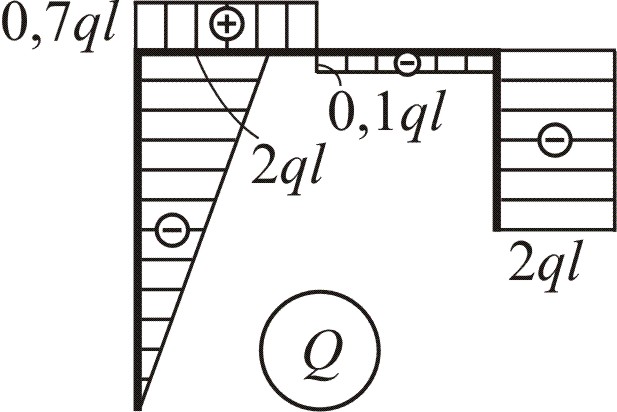
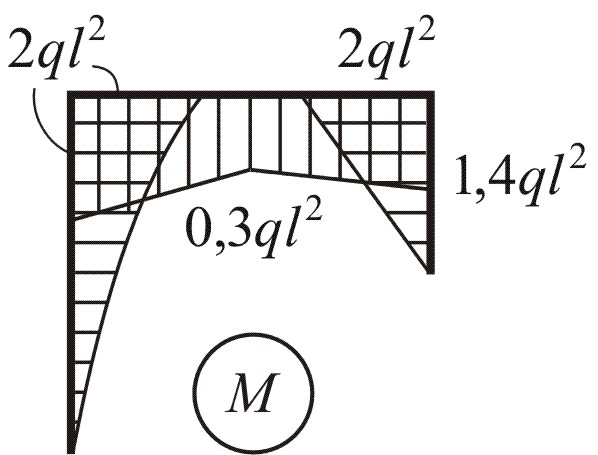
Откладывая полученные значения на схемах рамы, строим эпюры N, Q, M (рис. 4.2, а, б, в). Положительные значения ординат сил будем откладывать снаружи рамы, отрицательные – внутри. Эпюры изгибающих моментов строим на сжатых волокнах.

На 1-м участке эпюра N представляет собой прямоугольник с отрицательной ординатой N = – 0,7qa. Её откладываем справа от оси первого участка. Эпюра Q ограничена наклонной линией, проходящей через начало координат. Все ординаты отрицательные, откладываем их справа от оси рамы. Выражение М – квадратная парабола. Так как на эпюре Q наклонная линия не пересекает ось стержня, то на эпюре М будет кривая без перегиба. Строим эпюру М справа от оси первого участка.

На 2-м участке имеем отрицательные постоянные значения N и Q, поэтому на эпюрах откладываем значения вниз от оси рамы и строим прямоугольники; эпюра М ограничена наклонной прямой.

На 3 и 4-м участках характер эпюр сохраняется таким же, как и на втором участке. В точке приложения силы Р на эпюре Q имеется скачок, на эпюре М – излом навстречу силе.

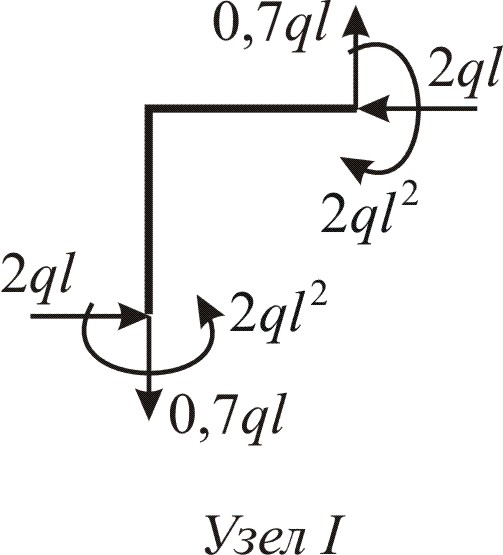
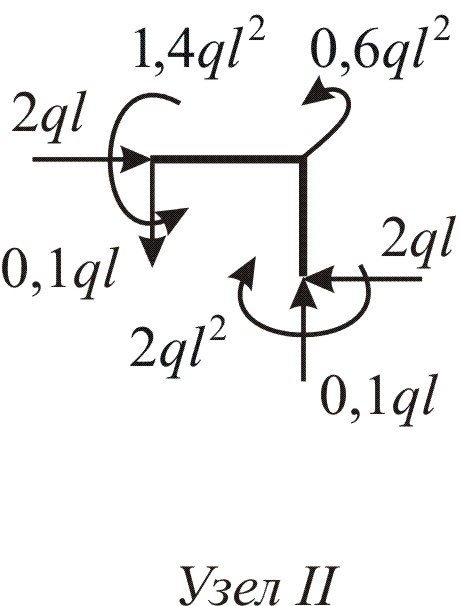
Правила контроля эпюр Q и М в рамах те же, что для балок. К обычным правилам контроля добавляется ещё одно: все узлы рамы должны находиться в равновесии под действием сил и изгибающих моментов. Используем это правило. Двумя бесконечно близкими сечениями вырежем узлы I и II (рис. 4.1, а), изобразим их отдельно, приложив в сечениях соответствующие внутренние усилия (рис. 4.3), значения которых берём из эпюр N, Q, M (рис. 4.2). Далее составляем уравнения равновесия по (4.2):

а – Узел I	б – Узел II

Рис. 4.3

Убеждаемся, что узел I находится в равновесии. Аналогично проверяется равновесие узла II (рис. 6.3, б).