3. Перехід до еквівалентної конгруенції, старший коефіцієнт якої дорівнює 1.

Знайдемо ціле число 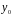таке, що 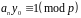. Оскільки 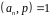, то конгруенція має єдиний розв'язок 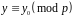, де – абсолютно найменший або найменший невід'ємний лишок класу 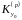за модулем . Число можна отримати також іншим способом: оскільки , то, в силу критерію взаємної простоти, існують цілі числа і 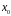такі, що 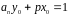. Тоді . Оскільки 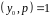, то, помноживши обидві частини конгруенції (3) на , отримуємо еквівалентну конгруенцію:

,

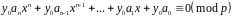в якій .

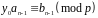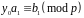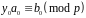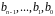Нехай , , …, , де – абсолютно найменші або найменші невід'ємні лишки за модулем . Замінивши в останній конгруенції коефіцієнти , …, , 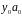на , а 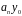на 1, отримуємо еквівалентну конгруенцію

.

Приклад 5. Замінити конгруенцію

,

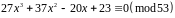на еквівалентну конгруенцію, старший коефіцієнт якої дорівнює 1.

Розв’язання. Розв’яжемо конгруенцію

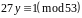
і знайдемо 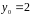. Дана конгруенція еквівалентна конгруенції

,

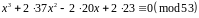тобто конгруенції

.

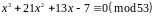3. Число розв’язків конгруенції -го степеня за простим модулем

При розв’язуванні конгруенцій (3) застосовуються теореми:

Теорема 1 (Безу-Горнера). Для будь-якого многочлен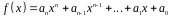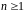а , , і числа 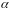, такого, що 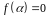, справедливо:

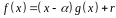
де , , , , .

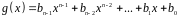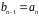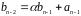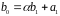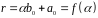Теорема 2 (про число розв’язків конгруенції -го степеня за простим модулем) Конгруенція -го степеня за простим модулем із старшим коефіцієнтом, що не ділиться на , може мати не більше ніж коренів.

Наслідок 1. Якщо деякі числа 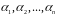становлять розв'язок конгруенції -го степеня, то ця конгруенція еквівалентна конгруенції

.

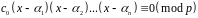Приклад 1. Розв’язати конгруенцію

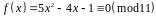
способом підбору абсолютно найменших лишків.

Розв’язання. Запишемо повну систему абсолютно найменших лишків за модулем :

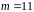0, 1, 2, 3, 4, 5, –5, –4, –3 ,–2, –1.

Підставимо числа цієї системи в дану конгруенцію. Будемо мати:

;

;

;

.

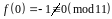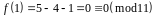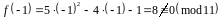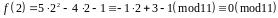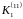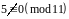Таким чином, лишки 0 і 2 задовольняють конгруенцію, отже, класи і є розв'язками даної конгруенції. В силу теореми 2, оскільки старший коефіцієнт , то конгруенція має не більше ніж 2 корені, тобто інших розв'язків дана конгруенція не має.

Приклад 2. Число 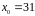є розв'язком конгруенції

.

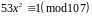Знайти всі розв'язки цієї конгруенції.

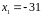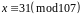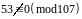Розв’язання. Очевидно, що разом із числом дану конгруенцію задовольняє число . Тому розв'язками даної конгруенції є і . Оскільки старший коефіцієнт , то конгруенція має не більше ніж 2 корені. Отже, розв'язками даної конгруенції є класи 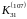і .

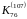Означення. Конгруенція

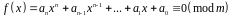
називається тотожною, якщо всі її коефіцієнти конгруентні нулю за модулем .

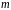Наслідок 2. Якщо конгруенція -го степеня за простим модулем

має більше ніж коренів, то вона є тотожною.

Теорема 3. (Вільсона). Якщо – просте число, то

.

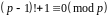Приклад 3. 1) , ;

2) , ;

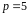3) , .

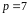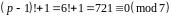Теорема 4. Якщо число – складене, то

.

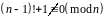Зауваження. Неважко показати, що якщо – складене число, 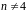, то .

Приклад 4. 1) , ;

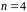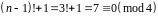2) , .

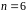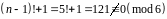Теореми 3 і 4 показують, що необхідною і достатньою умовами того, щоб число 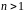було простим, є подільність 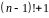на .