Если округлить результат до двух знаков, то

и

.

Используя формулы (24) и (25) и результаты примера 1, получим

;

;

< ;

Формула Симпсона. Предположим, что . Разделим отрезок на равных частей, тогда

, (26)

где ; ; ;

Заменим функцию на каждом из отрезков длиной по формуле Стирлинга второго порядка. Проводя рассуждения, аналогичные сделанным при выводе формуле трапеций, получим квадратурную формулу Симпсона

(27)

с остаточным членом

(28)

Оценка остаточной погрешности формулы Симпсона примет вид

, (29)

где

Вычислительная погрешность формулы Симпсона равна

(30)

Из выражения для остаточного члена формулы Симпсона следует, что она точна для многочленов третьей степени.

Пример 3. Вычислить по формуле Симпсона с точностью .

Применяя алгоритм решения задачи II, представим суммарную погрешность в виде суммы трех слагаемых

Выберем из условия

Так как = то

и, следовательно,

Таким образом, , и

Составим таблицу значений функций с пятью знаками после запятой

	0.000	0.125	0.250	0.375	0.500	0.625	0.750
	1.000	0.88889	0.800	0.72727	0.66667	0.61538	0.57143

	0.875	1.000
	0.53333	0.500

И спользуя формулу (27), получаем:

Округляя полученный результат, получим

Правило Рунге практической оценки погрешности квадратурных формул.

Пусть и интеграл (1) вычисляется по формуле прямоугольников. Наличие у производных и позволяет при выводе формулы прямоугольников (7)-(13) получить следующее полезное соотношение

(31)

где (32)

• постоянная, не зависящая от . Величина называется главной частью погрешности формулы прямоугольников.

Если , то справедливо аналогичное соотношение и для формулы трапеций

(33)

где (34)

не зависит от .

При условии можно получить аналогичные (31) и (33) соотношения для формулы Симпсона (35)

где - не зависящая от постоянная.

Обозначим через приближенное значение интеграла (1), найденное по одной из трех формул (12), (20), (27), и объединим соотношения (31), (33), (35) в одно

(36)

где не зависит от , для формул прямоугольников и трапеций, для формулы Симпсона. Предполагается, что . Запишем соотношение (36) для

(37)

вычтем из (37) (36) и получим

или

или

и, следовательно, с точностью до имеем

(38)

Вычисление приближенной оценки погрешности квадратурной формулы по формуле (38) называется правилом Рунге.

Уточнение приближенного решения по Ричардсону.

Вычитая из умноженного на равенства (36) равенство (37), получаем:

(39)

откуда (40)

Число (41)

называется уточненным по Ричардсону приближенным значением интеграла .

Согласно (40) (42)

Таким образом, с помощью приближенных значений интегралов найденных по соответствующим квадратурным формулам с шагом и , можно, во-первых, оценить погрешность более точного значения интеграла по правилу Рунге (38) и, во-вторых, вычислить по формуле (41) приближенное значение интеграла , имеющее погрешность более высокого порядка относительно , чем .

Вычисление интегралов с заданной степенью точности с помощью правила Рунге.

При применении алгоритма решения задачи II выбор шага интегрирования связан с решением неравенств либо (14), либо (22), либо (29), решение которых связано с нахождением что на практике не всегда возможно. Применение правила Рунге позволяет избежать этих трудностей.

Алгоритм вычисления интеграла с заданной степенью точности с автоматическим выбором шага.

1 шаг. Пусть – заданная функция, – интервал интегрирования, -допустимая точность.

2. шаг. Положить где для формул прямоугольников и трапеций, для формулы Симпсона;

; и кратно 2 или 4;

3 шаг. Вычислим

4 шаг. Положим и вычислим

5 шаг. Определим

6 шаг. Если , то положим и остановимся, иначе положим и перейдем к шагу 3.

Пример 4. Вычислить по формуле прямоугольников с точностью .

1 шаг. ; ; .

2 шаг. Положим , так как должно быть четным;

2. шаг. Составим таблицу значений функции в точках с тремя знаками после запятой.

	0,125	0,375	0,625	0,875
	0,985	0,877	0,719	0,566

4 шаг. Положим вычислим

.

5 шаг. Определим

6 шаг. Так как то положим .

Сравнение полученных результатов с точным значением интеграла показывает, что

,

следовательно, имеет 2 верных знака, а верных знака, что и следует из выражения (42).

Итак,

Пример 5. Вычислить по формуле Симпсона с точностью .

1. шаг. Положим 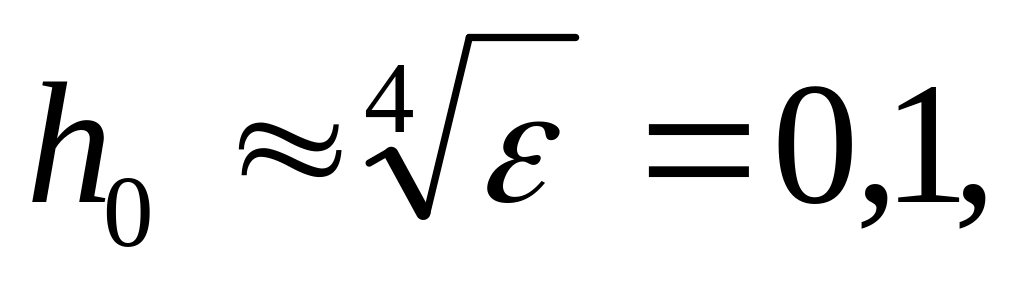тогда но так как должно быть кратным 4, то выберем ;

2. шаг. Составим таблицу значений функции в точках с шестью знаками после запятой.

	0,0	0,125	0,25	0,375	0,5
	1,000000	0,984615	0,941176	0,876712	0,8

	0,625	0,75	0,875	1,0
	0,719101	0,64	0,566372	0,500

Вычислим

4 шаг. Положим вычислим

.

5 шаг. Определим

6 шаг. Так как то вычислим и положим

ЗАДАЧА Г.

Вычислить интеграл по формуле прямоугольников с точностью 0,01.

1. 2. 3. 4.

5. 6. 7. 8.

9. .

Вычислить интеграл по формуле трапеций с точностью 0,01.

10. 11. 12. 13.

14. 15. 16. 17.

Вычислить интеграл по формуле Симпсона с точностью

18. 19. 20. 21.

22. 23. 24. 25. .