
- •Експериментальна частина
- •Хід виконання роботи
- •Обробка результатів вимірювання
- •Опис експериментальної установки.
- •Хід виконання роботи
- •Обробка результатів вимірювання
- •Контрольні питання
- •Опис роботи лабораторної установки
- •Хід виконання роботи
- •Обробка результатів вимірювання
- •Контрольні питання
- •Хід виконання роботи
- •Завдання 1
- •Вимірювання
- •Обробка результатів вимірювання
- •Завдання 2
- •Вимірювання
- •Обробка результатів вимірювання
- •Завдання 3
- •Контрольні питання
- •Градуювання шкали спектрометра по лінійчатому спектру неона й вивчення спектра атома водню Мета роботи
- •Прилади та обладнання
- •Коротка теорія
- •Опис експериментальної установки
- •Хід виконання роботи
- •Обробка результатів вимірювання
- •Контрольні питання
- •Додаток § 7. Теплове випромінювання та його рівноважність
- •§ 8. Закони теплового випромінювання
- •2. Закон Cтефана - Больцмана.
- •§ 9. Оптична пірометрія
- •§ 10. Явище фотоефекта.
- •§ 11. Розрахунок воднеподібних атомів
- •1. Квантовий розрахунок воднеподібних атомів.
- •2. Розрахунок воднеподібних атомів за Бором.
§ 8. Закони теплового випромінювання
1. Закон Кірхгофа. Дослідним шляхом Кірхгоф установив, що відношення випромінювальної здатності тіл до їх поглинальної здатності при температурі Т на частоті не залежить від природи тіла й визначається універсальною функцією частоти й температури тіла
![]() ,
(1)
,
(1)
де
![]() випромінювальна
здатність АЧТ. Функцію
називають також універсальною функцією
Кірхгофа. Залежність функції Кірхгофа
від частоти представлена на Мал.41.
випромінювальна
здатність АЧТ. Функцію
називають також універсальною функцією
Кірхгофа. Залежність функції Кірхгофа
від частоти представлена на Мал.41.
М.Планк в 1900 р встановив (див. нижче) явний вид функції Кірхгофа
 ,
(2)
,
(2)
д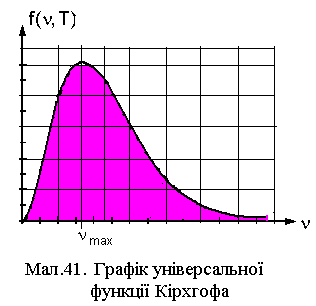 е
е
![]()
стала Планка,
стала Планка,
![]()
швидкість поширення світла у вакуумі,
швидкість поширення світла у вакуумі,
![]()
стала Больцмана.
стала Больцмана.
Знаючи поглинальну здатність тіла, із (1) можна одержати вираз для випромінювальної здатності
![]() ,
,
а потім і енергетичну світність тіла
![]() .
.
Розподіл поглинальної здатності по частоті тіла можна одержати експериментально, а інтегрування провести чисельними методами.
2. Закон Cтефана - Больцмана.
Абсолютно чорне тіло. Закон Cтефана - Больцмана для абсолютно чорного тіла енергетичну світність R* як функцію температури так
![]() ,
(3)
,
(3)
де
![]()
стала Стефана-Больцмана. Цей закон
експериментально установив в 1879 році
Й.Стефан, а теоретичне обґрунтування у
1884 році дав Л.Больцман.
стала Стефана-Больцмана. Цей закон
експериментально установив в 1879 році
Й.Стефан, а теоретичне обґрунтування у
1884 році дав Л.Больцман.
Сірі
тіла.
У
природі практично усі тіла мають
поглинальну здатність
![]() і їх називають сірими. Існують сірі
тіла, поглинальна здатність яких у
широкому діапазоні частот є сталою
величиною
і їх називають сірими. Існують сірі
тіла, поглинальна здатність яких у
широкому діапазоні частот є сталою
величиною
![]() .
Для таких тіл випромінювальна здатність
пропорційна випромінювальній здатності
абсолютно чорного тіла
.
Для таких тіл випромінювальна здатність
пропорційна випромінювальній здатності
абсолютно чорного тіла
![]() ,
(4)
,
(4)
а їх енергетична світність може бути записана у вигляді
![]() .
.
4.
Закон зміщення Віна.
Він довів, що положення максимуму
![]() універсальної функції Кірхгофа
універсальної функції Кірхгофа
![]() задовольняє співвідношенню
задовольняє співвідношенню
T = b, (5)
де
Т
температура тіла,
![]()
стала Віна. Це означає, що при підвищенні
температури тіла максимум його теплового
випромінювання зміщується в бік менших
довжин хвилі (величина
зменшується) і навпаки.
стала Віна. Це означає, що при підвищенні
температури тіла максимум його теплового
випромінювання зміщується в бік менших
довжин хвилі (величина
зменшується) і навпаки.
5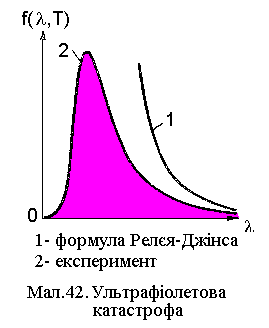 .
Формула Релея - Джінса.
З точки зору класичної фізики,
випромінювання АЧТ можна представити
як реалізацію сукупності просторових
стоячих електромагнітних хвиль в
обмеженому об’ємі з відповідними
частотами. Останні визначаються
граничними умовами. Число
.
Формула Релея - Джінса.
З точки зору класичної фізики,
випромінювання АЧТ можна представити
як реалізацію сукупності просторових
стоячих електромагнітних хвиль в
обмеженому об’ємі з відповідними
частотами. Останні визначаються
граничними умовами. Число
![]() таких стоячих хвиль на частоті
в одиничному об’ємі при двох можливих
поляризаціях дорівнює
таких стоячих хвиль на частоті
в одиничному об’ємі при двох можливих
поляризаціях дорівнює
![]() .
(6)
.
(6)
Вважаючи,
що на кожну коливальну ступінь свободи
приходиться енергія кТ, енергію в
інтервалі частот від
![]() можна записати у вигляді
можна записати у вигляді
![]() ,
(7)
,
(7)
Тепер випромінювальну здатність АЧТ можна одержати у вигляді
![]() .
.
або
![]() .
(8)
.
(8)
Вираз (8) є формулою Релея- Джінса. В
області великих частот (малих
довжин хвиль
)
енергетична світність за (8) прямує до
нескінченності, що різко розходиться
з експериментом (див.![]() ).
Цю розбіжність у класичній фізиці
названо ультрафіолетовою катастрофою.
).
Цю розбіжність у класичній фізиці
названо ультрафіолетовою катастрофою.
6.
Гіпотеза та формула Планка.
В 1900 році М.Планк висунув гіпотезу, що
енергія електромагнітного поля є
дискретною і складається з порцій
(квантів) енергії
![]() .
Пізніше було встановлено, що
.
Пізніше було встановлено, що
![]() ,
(9)
,
(9)
де стала
![]() ,
,
називається перекресленою або просто сталою Планка, або сталою Дірака, який увів її уперше. Повна енергія випромінювання на частоті кратна (9) і дорівнює
![]() .
(10)
.
(10)
З цієї точки зору Планк розглянув випромінювальну здатність абсолютно чорного тіла і одержав випромінювальну здатність АЧТ у виді
 .
(11)
.
(11)
Одержаний
вираз для
![]() називається формулою
Планка.
називається формулою
Планка.
Формула Планка точно узгоджується з експериментом у всьому
діапазоні
частот
.
З неї випливає закон Віна, а при умові
![]() маємо
маємо
![]() і формула Планка переходить у формулу
Релея-Джінса (8). За формулою Планка можна
розрахувати сталі Стефана-Больцмана
та сталу Віна.
і формула Планка переходить у формулу
Релея-Джінса (8). За формулою Планка можна
розрахувати сталі Стефана-Больцмана
та сталу Віна.
