2.2 Парная нелинейная регрессия

Мы достаточно подробно описали как способы вычисления параметров линейной регрессии, так и способы оценок качества моделей, которые можно построить с ее использованием. Однако далеко не все зависимости, в том числе зависимости, часто встречающиеся в экономических задачах, носят линейный характер. И возникает естественный вопрос – а как нам поступать в подобных случаях?

2.2.1 Распространение методов парной линейной регрессии на нелинейные задачи

Есть ряд характерных экономических задач, требующих нелинейных зависимостей для своего описания. Например, для описания зависимости спроса на товар от семейного дохода (кривые Энгеля) используются зависимости:

(2.10)

(2.11)¹⁹

В приведенных примерах зависимости объясняемой переменной Y от объясняющей переменной Х очевидно нелинейны. Однако обе эти зависимости содержат всего два параметра, подлежащих определению. А это дает нам шанс воспользоваться линейным регрессионным анализом. Действительно, первое из этих уравнений (2.10) нелинейно по Х, но линейно по искомым параметрам ₁ и ₂. Следовательно достаточно вместо объясняющей величины Х ввести новую объясняющую величину и мы получим хорошо нам знакомый вид зависимости: Y= ₁ + ₂ Z, и далее весь аппарат линейной регрессионной модели прекрасно работает.

Вполне очевидно, что подобный подход применим не только к зависимости типа (2.10), но ко всем зависимостям типа: Y= ₁ + ₂ f(X), где f(X) – функция, строго монотонная на интересующем нас интервале²⁰; достаточно перейти к новой объясняющей переменной Z= f(X), – и мы получим хорошо нам знакомую линейную модель Y= ₁ + ₂ Z.

Более того, предлагаемый подход можно расширить на боле сложные двухпараметрические модели, если допустить замену не только объясняющей, но и объясняемой переменной. Например, пусть предполагаемая зависимость между нашими переменными имеет вид:

Y= ₁ X + ₂ X^3.

Разделив обе части этого равенства на , получим следующую зависимость:

Если теперь сделать двойную замену переменных, заменив X² на Z, а на W, то получим для новых переменных линейную зависимость:

Случай, представленный формулой (2.11) выглядит более сложным, т.к. параметр зависимости ₂ входит в формулу нелинейным образом. Однако и в этом случае можно подобрать подходящую замену переменных. В самом деле, эта формула описывает зависимость с постоянной эластичностью, равной ₂. А зависимости постоянной эластичностью становятся линейными в логарифмическом масштабе. Следовательно, если осуществить двойную логарифмическую замену: W = lg(Y), Z = lg(X), а также ввести обозначение: ₀ = lg(₁), мы увидим, что нелинейная двухпараметрическая зависимость (2.11) превратится в хорошо нам знакомую линейную модель

W = ₀ + ₂ Z

Как мы видим, спектр применения модели линейной регрессии оказывается гораздо более широким, чем это кажется на первый взгляд.

Приведем в заключение таблицу наиболее часто встречающихся нелинейных зависимостей, которые определенными взаимно однозначными преобразованиями переменных могут быть приведены к линейной модели.

Исходная зависимость	Искомые параметры	Преобразованная зависимость	Введенные вспомогательные величины
	1, 2	W = 0 + 2 Z	W = lg(Y), Z = lg(X), 0 = lg(1)
	1, 2	Y= 1 + 2 Z
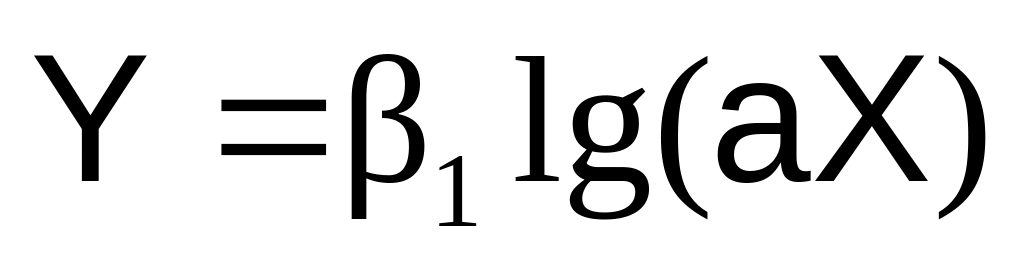
	1, a	Y= 2 + 1 Z	Z = lg(X), 2 = 1 lg(a)
Y= 1 X + 2 X3	1, 2	W = 1 + 2 Z	W = , Z = X2,
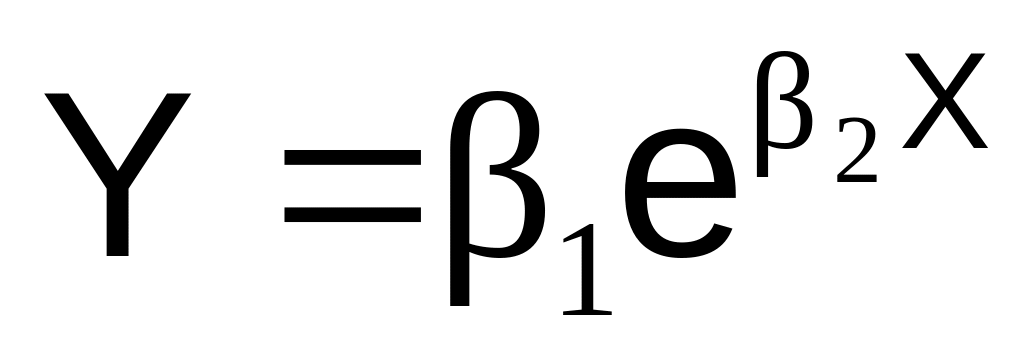
	1, 2	W = 0 + 2 X	W = ln(Y), 0 = ln(1)