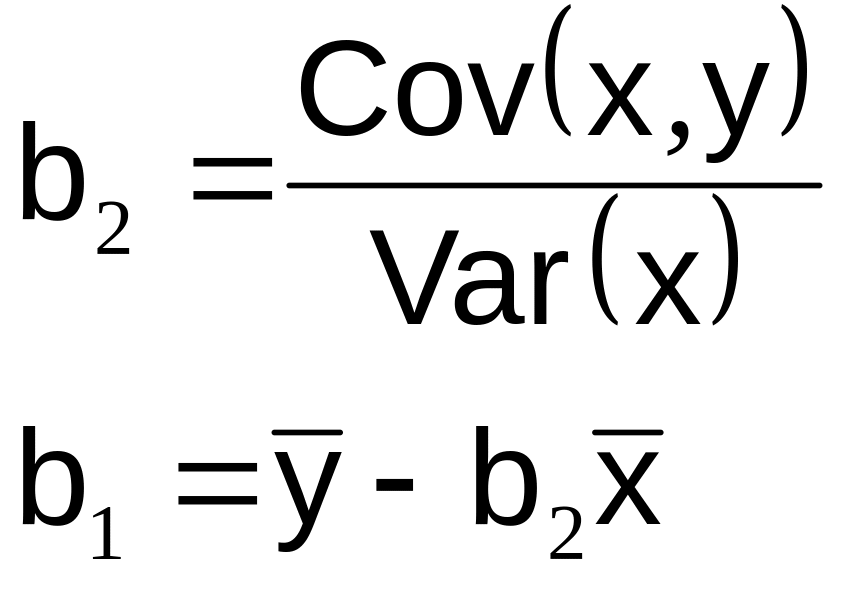2.1.2 Мера оценки отклонений – метод наименьших квадратов (мнк).

Итак, мы располагаем некоторой таблицей данных {x_i,y_i} (набором точек на плоскости P_i(x_i,y_i) ), наша цель провести на плоскости прямую таким образом, чтобы она была максимально близка к нашему набору точек.

Пусть уравнение такой прямой имеет вид: – здесь мы через обозначили значения на модельной прямой, мы пометили их знаком «^», чтобы отличать от полученных опытным путём значений y_i. Как только мы проведем любую прямую, у нас в каждой точке появятся отклонения (ошибки модели, их называют также ошибками аппроксимации) ε_i = y_i – , наша задача состоит теперь в том, чтобы так подобрать коэффициенты модели b₁ и b₂, чтобы минимизировать отклонения в совокупности. Проблема в том, как оценить всю совокупность отклонений.

Достаточно очевидно, что сумма отклонений не есть подходящая мера. Ведь достаточно провести горизонтальную прямую на уровне среднего значения , чтобы сумма отклонений стала равна нулю, однако такую прямую трудно считать хорошей моделью. Тут дело в том, что положительные и отрицательные отклонения при таком подходе взаимно гасят друг друга, а наша цель не допустить больших отклонений модели от опытных данных независимо от знака этих отклонений.

Чтобы уничтожить влияние знака, разумно суммировать не сами отклонения ε_i, а их квадраты, т.е. минимизировать не , а . Принятие такого критерия оптимальности искомой прямой носит название метода наименьших квадратов (МНК), как мы увидим в дальнейшем такой подход действительно дает оптимальные результаты, при соблюдении некоторых условий, которые в реальности достаточно часто действительно выполнены.

Итак, мы можем теперь четко сформулировать задачу. Пусть в результате некоторых опытов мы располагаем набором из n данных для двух величин: {x_i,y_i}. Найти такие два коэффициента b₁ и b₂, чтобы сумма квадратов отклонений величин от опытных значений y_i была минимальной

(2.2)

Обратим внимание, что в роли неизвестных тут у нас выступают именно параметры искомой прямой b₁ и b₂, ведь все значения {x_i,y_i} нам известны. Если мы подставим все величины, входящие в третью сумму в формуле (2.2), и выполним все арифметические действия, то увидим, что функция представляет собой просто многочлен второй степени относительно b₁ и b₂. Чтобы найти его минимум нужно просто вычислить его частные производные по b₁ и b₂ и приравнять их нулю. Когда мы это сделаем, то получим два уравнения с двумя неизвестными. Решение этих уравнений дает следующий результат:

(2.3)

Это и есть выражение для коэффициентов линейной регрессии, которые дает метод наименьших квадратов (МНК).

2.1.3 Практические вычисления для линейной модели.

Теперь мы располагаем всем необходимым для того, чтобы построить практическую схему вычислений. Нарисуем таблицу:

xi	yi	xi2	xi yi		εi
x1	y1	x12	x1 y1		ε1 = y1–
x2	y2	x22	x2 y2		ε2 =y2–
x3	y3	x32	x3 y3		ε3 =y3–
…	…	…	…	…	…
xn	yn	xn2	xn yn		εn =yn–

После заполнения столбцов x_i, y_i, вычисляем элементы двух следующих столбцов: x_i² и x_iy_i . Далее, по приведенным в таблице формулам вычисляем Var(x), Cov(x,y), затем b₁ и b₂, и после этого заполняем два последних столбца