2. Определение возмущающих сил

Связь между координатами в системах 0⁰⁰⁰⁰ и 0 записывается в виде:

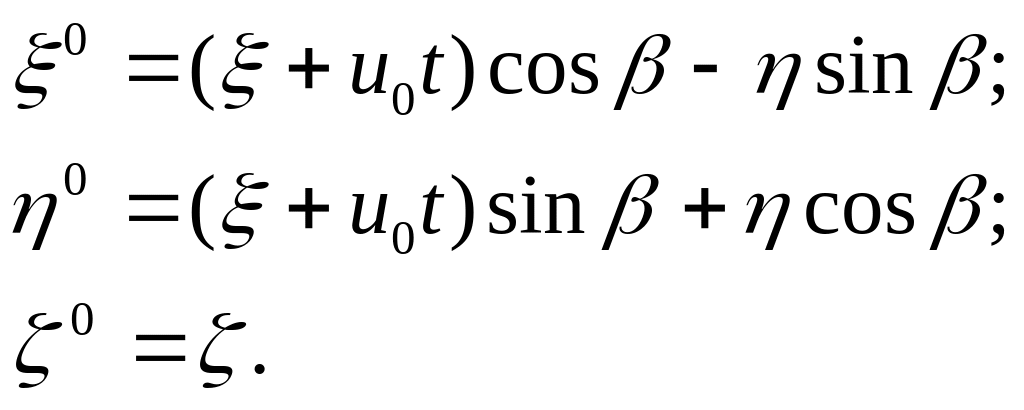(16)

Поэтому выражение для волновой поверхности в системе координат 0 можно переписать как

, (17)

а выражение для угла волнового склона -

, (18)

или

; (19)

. (20)

В этих выражениях введена кажущаяся частота волны

. (21)

В ней учитывается влияние скорости хода и курсового угла. Именно с такой частотой набегающее волнение и будет действовать на корабль.

Полунеподвижная система координат 0 и система координат Gxyz свя-заны между собою через перемещения корабля при качке. В рамках линейной теории характеристики волнения, в частности, величина k = , и характеристики качки корабля – малые первого порядка, поэтому с точностью до малых 2-го порядка можно считать, что . Тогда выражения (19) - (20) перепишутся в виде:

(22)

Выражения (22) дают возможность определять действующие на корабль возмущающие силы при набегании волнения под произвольным курсовым углом.

Рассмотрим корабль, стоящий лагом к волнению, причем волны будут набегать с правого борта. В этом случае и

(23)

Для корабля, ширина и осадка которого сравнимы с длиной волны, выра-жения и в пределах ширины В и осадки Т будут иметь конечное значение, а величины в пределах ширины и осадки будут переменными. Такой корабль называется кораблем конечных размеров.

Есл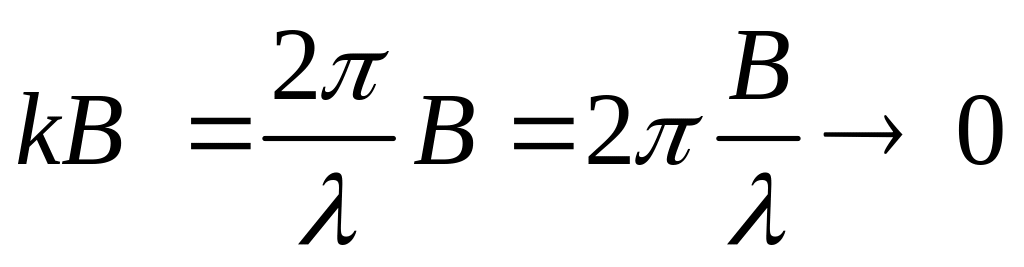и и , корабль называется кораблем бесконечно малых размеров (как мы видим, для такого корабля ширина и осадка малы по сравнению с длиной волны). При этом выражения (23) упростятся и будут иметь вид:

(24)

т.е. волновая поверхность в пределах ширины остается плоской.Корабль уподобляется частице воды и участвует в волновом движении как частица воды. Такой подход был предложен впервые Фрудом в 19-м веке.

Для корабля бесконечно малых размеров возмущающие силы легко выводятся с использованием принципа относительного движения.

Рассмотрим вначале вертикальную качку (рис. 2). корабль переместится от начального положения на величину со скоростью и ускорением , но за это время волновая поверхность переместится на расстояние cо скоростью и ускорением .

Соответственно все гидромеханические силы будут зависеть от относи-тельных параметров качки. Тогда уравнение качки на тихой воде можно записать в форме Лагранжа

. (25)

Перенесем часть членов в левую часть уравнения

. (26)

Если подставить из (24), а также и , получим уравнение вертикальной качки корабля беско-нечно малых размеров на волнении

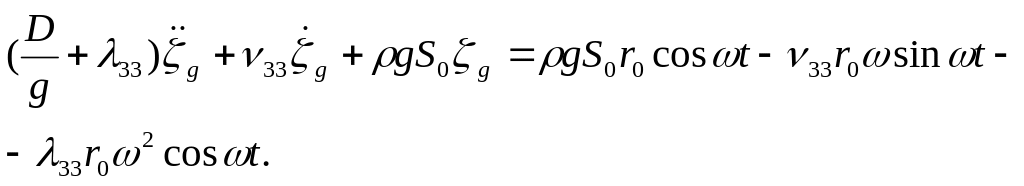(27)

В левой части уравнения стоят члены, описывающие качку на тихой воде, в правой - члены, зависящие от характеристик волнения - возмущающие силы. Если волн нет, в правой части будет 0.

Первая составляющая, пропорциональная перемещению имеет гидро-статическую природу. Она называется крыловской силой. Получить ее можно по гипотезе Крылова о том, что корабль своим присутствием не иcкажает набегающую волну, т.е. является как бы проницаемым. Эту силу также называют главной, так как для обычных кораблей на ее долю приходится до 80% суммарной возмущающей силы.

Вторая и третья составляющие называются дифракционными силами. Они учитывают искажение поля давлений в волне из-за присутствия корабля. Сила пропорциональна коэффициенту сопротивления (демпфирования) и называется демпфирующей частью дифракционной составляющей, а сила называется соответственно инерционной частью дифракционной составляющей.

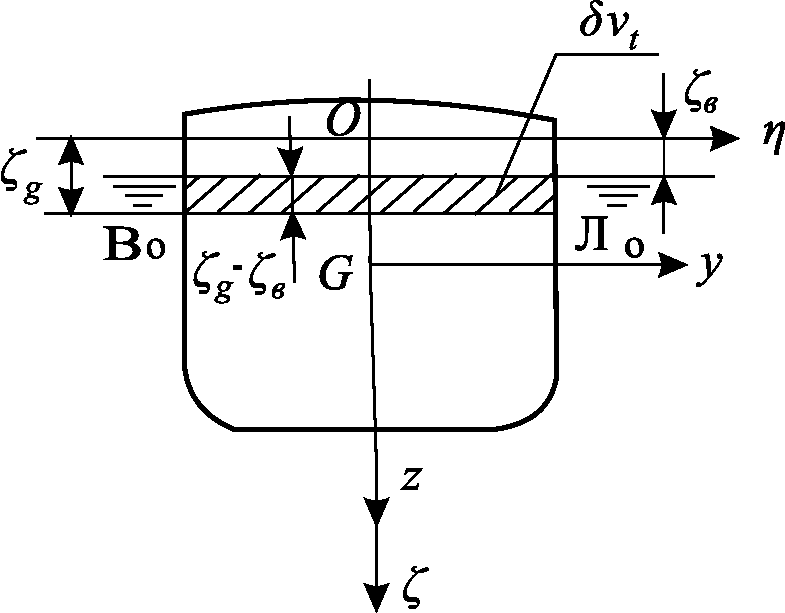
При выводе уравнений бортовой качки корабля проводим аналогичные рассуждения (рис. 3). Корабль наклоняется на угол с угловой скоростью и угловым ускорением . За это время волновая поверхность наклоняется на угол с угловой скоростью и угловым ускорением . Относительное перемещение корабля будет происходить на угол с угловой скоростью и угловым ускорением .

Уравнение Лагранжа для бортовой качки можно записать в виде:

. (28)

Перенесем часть членов уравнения в левую часть

. (29)

Рис. 2 Определение возмущающих сил при вертикальной качке

Подставим в (29) , и получим уравнение бортовой качки корабля бесконечно малых размеров

(30)

В правой части уравнения (30) стоят следующие составляющие возму-щающего момента:

- крыловская (главная) составляющая возмущающего момента;

- демпфирующая часть дифракционной составляющей;

- инерционная часть дифракционной составляющей.

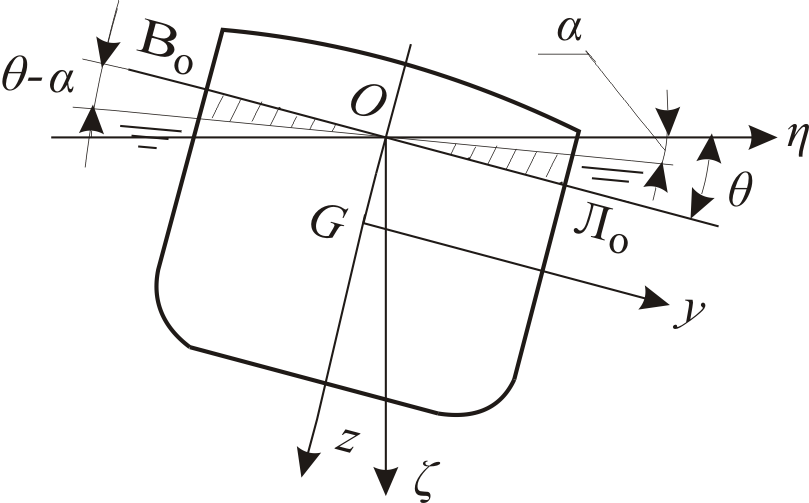
Рис. 3.Определение возмущающих моментов при бортовой качке