Министерство образования и науки Российской Федерации

Московский государственный машиностроительный университет «МАМИ»

Кафедра прикладной и вычислительной математики

имени Э.И. Григолюка

Балакирев Ю.Г.

Учебное пособие

по выполнению расчетно-графической работы по математике

Ряды Фурье. Уравнения математической физики.

2012

УДК 519.61

ББК 22.193

Рецензент:

к.ф.- м.н., проф. Е.А. Коган (Московский государственный машиностроительный университет «МАМИ»).

Балакирев Ю.Г. Ряды Фурье. Уравнения математической физики. Учебное пособие по выполнению расчетно-графической работы. – М.: МГМУ «МАМИ», 2012 – 24с.

В учебном пособии приведены решения типовых задач РГР по разделу математики «Ряды Фурье. Уравнения математической физики». Основное внимание уделяется развитию практических навыков получения решения дифференциальных уравнений математической физики в частных производных с использованием разложения функций в ряд Фурье. Изложенный материал должен служить студентам примером оформления РГР. Сложность решаемых уравнений соответствует сложности заданий в пособии [1].

М осковский Государственный машиностроительный университет «МАМИ», 2012

Введение

Данное пособие призвано помочь студенту выполнить расчетно-графическую работу по разделу высшей математики «Ряды Фурье. Уравнения математической физики», включенному в программу четвертого семестра технического университета. Необходимые теоретические сведения по этому разделу высшей математики, адаптированные для технических университетов, приведены в учебном пособии [1]. Для углубленного изучения теоретических основ этого раздела можно рекомендовать университетский курс уравнений математической физики [2]. Основное внимание в данном пособии обращается на последовательные рассуждения и соответствующие выкладки в процессе решения заданий. Кроме того, пособие служит примером оформления выполненной расчетно-графической работы по данному разделу математики.

Задание №1. Разложить функцию в ряд Фурье

Справка из теории рядов Фурье. Рядом Фурье по гармоническим функциям на симметричном относительно начала координат отрезке может быть представлена функция , удовлетворяющая условиям Дирихле (условия «гладкости»). В соответствии с этими условиями разлагаемая в ряд функция в пределах отрезка является кусочно-монотонной и ограниченной. Это означает, что конечным числом точек весь отрезок может быть разбит на интервалы , в пределах каждого из которых функция непрерывна и монотонна, т.е. не убывает или не возрастает. На границах выделенных интервалов функция может иметь разрывы первого рода, т.е. её пределы при стремлении аргумента справа и слева к каждой границе могут не совпадать, но они конечны.

Гармонические функции образуют полную сис­тему линейно независимых взаимно ортогональных функций на отрезке , т.е. при (везде, кроме последнего интеграла)

.

Ряд Фурье по выбранной системе гармонических функций имеет вид:

_(1.1)

Проверим ортогональность выбранных гармонических функций.

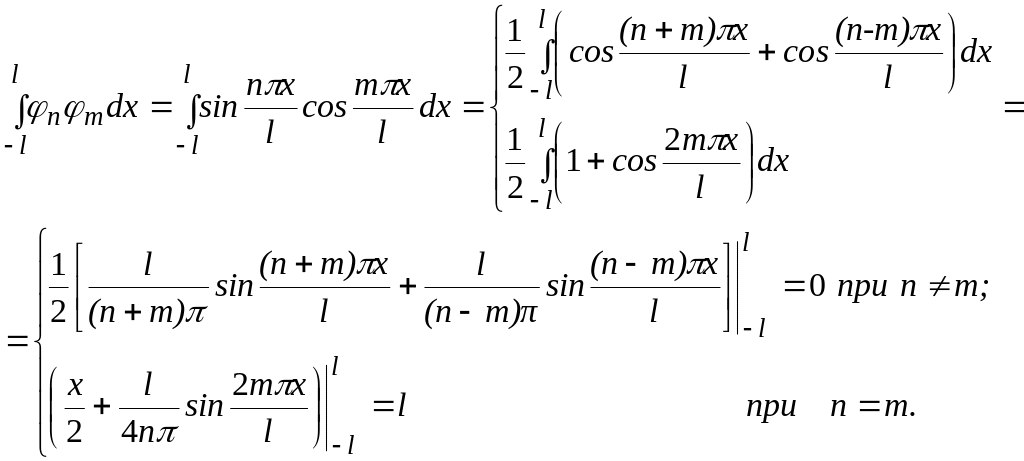
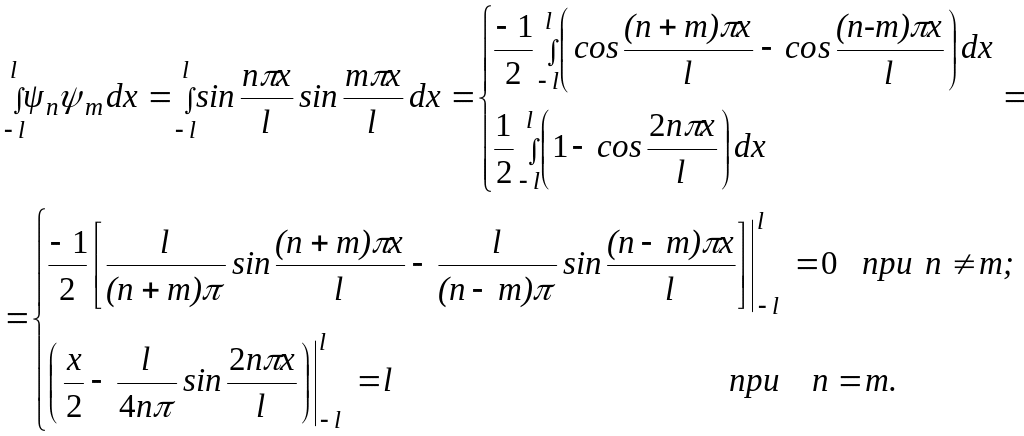
Выписанные условия ортогональности используемых функций (эти функции часто называют координатными или базисными функциями) значительно упрощают процедуру определения коэффициентов искомого ряда из соотношения (1.1). Последовательно умножая левую и правую части этого соотношения на каждую из координатных функций и выполняя интегрирование в пределах участка , получим систему линейных алгебраических уравнений для определения коэффициентов разложения функции в ряд.

Описанная процедура часто называется процедурой ортогонализации или процедурой проектирования уравнения (1.1). Нормой выбранных координатных функций являются величины

, ,

.

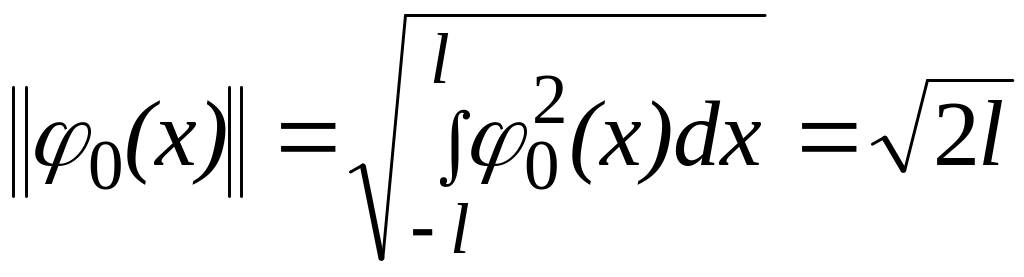Ортонормированной системой функций называется система, все функции которой взаимно ортогональны и имеют норму, равную единице. Ортонормированная система функций, полученная из выбранной выше системы ортогональных функций, имеет вид: .

С учетом условий ортогональности координатных функций в результате выполнения процедуры ортогонализации уравнения (1.1) к каждой координатной функции получим следующую систему алгебраических уравнений для вычисления коэффициентов разложения :

(1.2)

Итак, выражения для коэффициентов разложения заданной функции в ряд Фурье имеют вид:

(1.3)

Примечание. В учебном пособии [1] разложение функции в ряд Фурье записывается в виде:

(1.4)

Коэффициенты при координатных функциях в выражениях (1.1) и (1.4), естественно, совпадают. Появление двойки в знаменателе первого слагаемого требует увеличения вдвое числителя этого члена, т.е. , что делает одинаковыми множители при интегралах при вычислении . В этом и состоит идея использования формулы (1.4).

Если функция на отрезке является четной, то коэффициенты равны нулю, а в формулах для имеем в этом случае .

Если функция на отрезке является нечетной, то коэффициенты равны нулю, а в формулах для имеем в этом случае .

При распространении ряда Фурье на всю область значений аргумента получим периодическую функцию с периодом . Значения ряда Фурье при в точках непрерывности функции совпадает со значением этой функции, а в точках разрывов первого рода равны полусумме значений (пределов) функции справа и слева от границы.

Р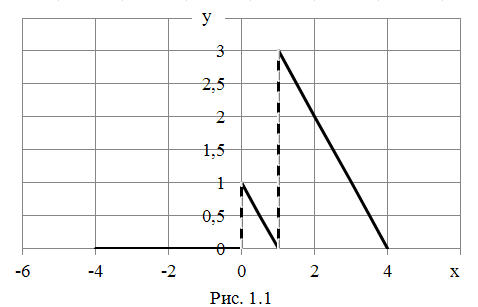 ешение. Заданная функция (рис. 1.1) удовлетворяет условиям Дирихле. На от­резке она ограничена, име-ет три уча­стка монотонно­сти: при она постоянна (не возрастает и не убывает); при и при она мо­нотонно убывает, а при и при имеет точки разрыва первого рода.

Заданная ни четная и ни нечетная функция, удовлетворяющая условиям Дирихле, на симметричном относительно начала координат участке длиной разлагается в ряд Фурье. Вычислим коэффициенты разложения функции в ряд Фурье по формулам (1.3).

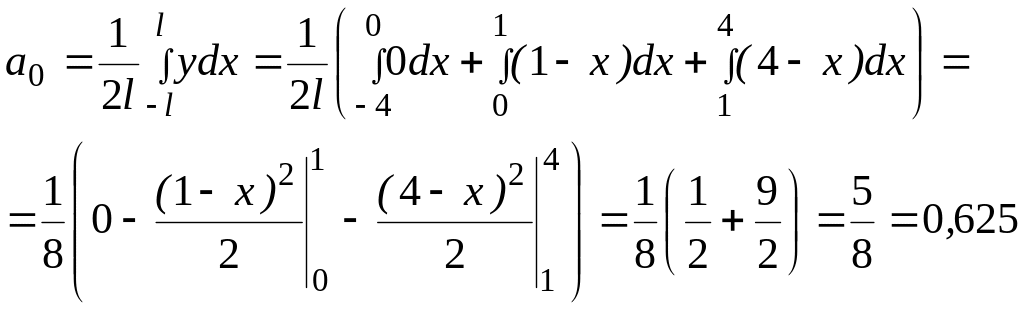
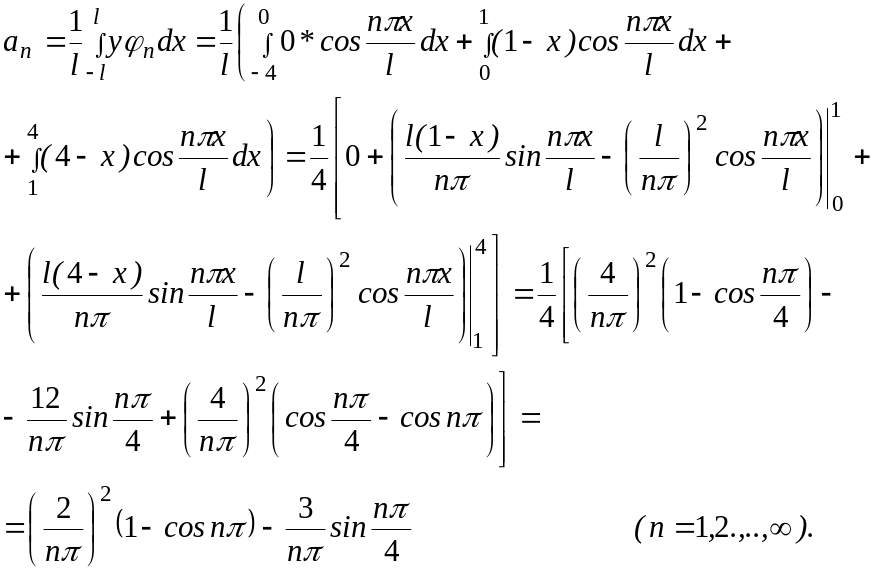
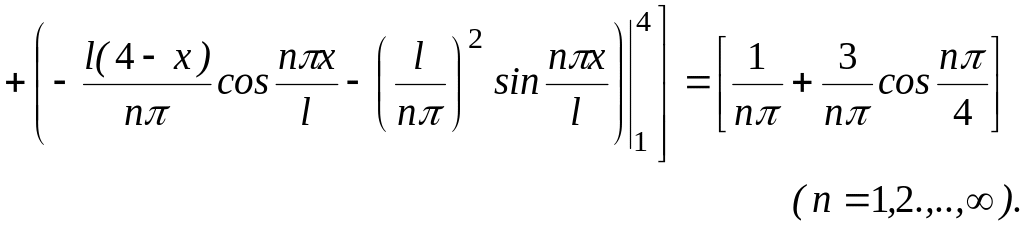
Ответ: Итак, имеем:

Задание №2. В виде ряда Фурье найти решение краевой задачи

Р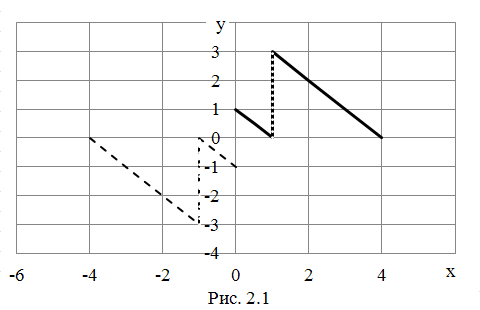 ешение. Данная задача иллюстрирует получение решения краевой задачи для неоднородного линейного дифференциального уравнения второго порядка с помощью разложения правой части в ряд Фурье. Решение может быть получено при произвольной правой части , удовлетворяющей условиям Дирихле и при произвольных граничных условиях.

1. Функция (сплошная линия на рис. 2.1) на отрезке длиной удовлетворяет условиям Дирихле (имеет два участка монотонного убывания и два разрыва первого рода) и может быть разложена в ряд Фурье. Эту функцию можно распространить на симметричный относительно начала координат отрезок как нечетную функцию, т.е. ) (рис.2.1). В этом случае функция разлагается в ряд Фурье по синусам.

Если распространить функцию на отрезок как функцию четную (рис. 2.2), то функция разлагается в ряд Фурье по косинусам.

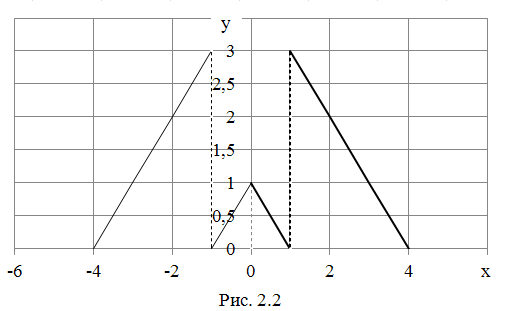
Пусть функция распространена на симметричный относительно начала координат отрезок как нечетная функция, т.е. ) (рис. 2.1). В этом случае функция на отрезке имеет три разрыва первого рода при значениях аргумента . На участках она монотонно возрастает, а на участках она монотонно убывает. Нечетная функция представляется рядом Фурье по синусам.

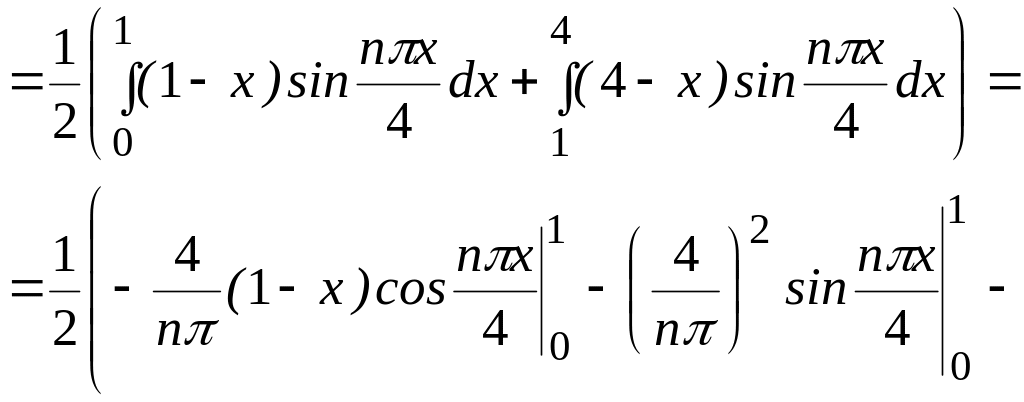
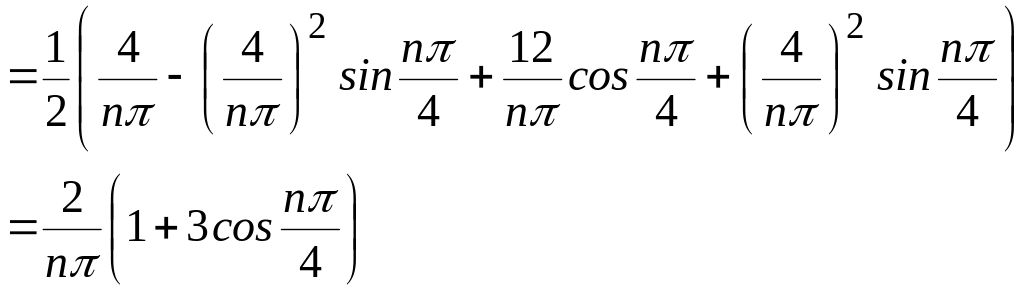
Итак

2. Требуется решить краевую задачу

Общее решение уравнения имеет вид:

Подставляя это решение в граничные условия, получим систему уравнений для определения произвольных констант .

Из этой системы имеем:

Ответ : Решение краевой задачи имеет вид:

Правильность решения проверяется подстановкой его в уравнение и в граничные условия. В данном примере эта процедура достаточно тривиальна.

Задание №3. Разложить функцию в обобщенный ряд Фурье по собственным функциям краевой задачи

Решение. 1. Определение собственных функций краевой задачи

Общее решение уравнения .

Подставляя решение в граничные условия, получим однородную систему алгебраических уравнений для определения произвольных констант .

Условием существования ненулевых решений этой системы уравнений равенство нулю определителя матрицы системы:

.

Из этого условия получаем собственные значения краевой задачи:

Этим собственным значениям соответствуют следующие собственные функции

Для собственных функций введена нормировка, при которой . Отметим, что при найденных собственных значениях из системы алгебраических уравнений следует .