5.Принадлежность точки прямой; прямой – плоскости; точки – плоскости. Конкурирующие точки. Определение видимости на чертеже.

Точка А принадлежит прямой l если ее проекции на эпюре принадлежат одноименным проекциям прямой. (рис. 50)

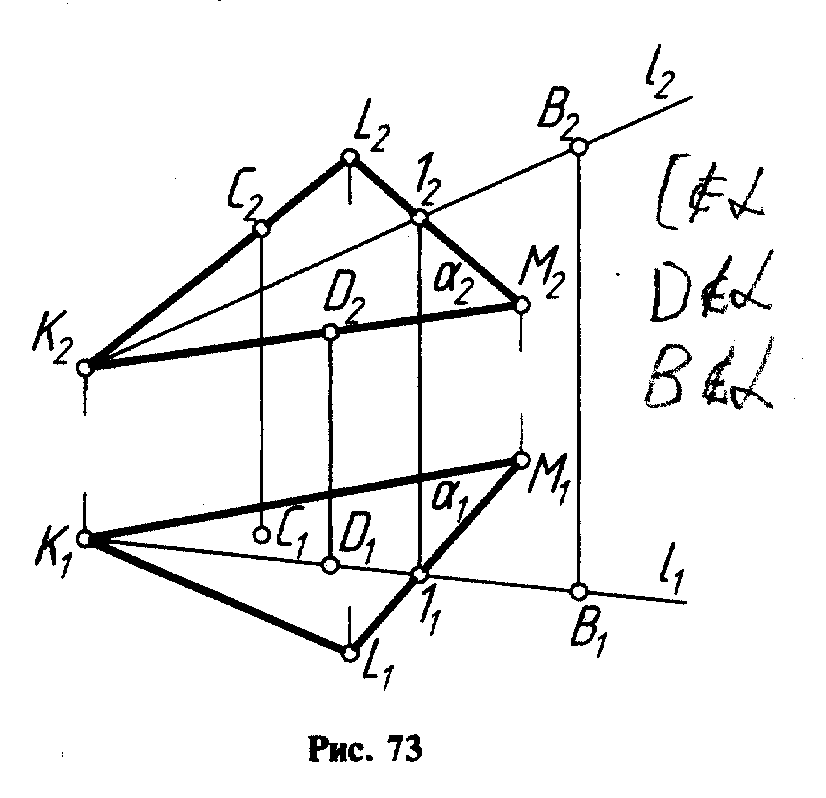
Прямая принадлежит плоскости, если две ее точки принадлежат этой плоскости. На рис. 73 прямая (KLM), так как точки К и 1 прямой l принадлежат плоскости, заданной KLM.

Точка принадлежит плоскости, если она лежит на прямой находящейся в этой плоскости.

Точки, имеющие одну пару совпавших одноименных проекций, называются конкурирующими.Если совпадают горизонтальные проекции точек (рис. 44), то точки Е и F называют горизонтально конкурирующими. Точки G и H называют фронтально конкурирующими, так как G₂ Н₂ (рис. 44). C помощью конкурирующих точек определяют видимость на чертежах.

6.Теорема о проецировании угла перпендикулярного к плоскости. Плоскость перпендикулярная заданной плоскости.

Теорема о проецировании угла справедлива для пересекающихся и скрещивающихся прямых.

Прямой угол проецируется в прямой если одна из его сторон параллельна плоскости, а вторая не являеться проецирующей.

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой (рис. 132).

Через точку А проводим h, а через С – f.

Через произвольную точку D на прямой l проводим перпендикуляр m к плоскости АВС.

и

Из этого следует, что получившаяся с помощью 2-х прямых l и m плоскость .

7. Линия наибольшего наклона плоскости общего положения к горизонтальной, фронтальной и профильной пл. Проекции.

Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j, которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций. Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее. 

Линия ската всегда перпендикулярна к горизонтали данной плоскости. Линия наибольшего наклона к произвольной плоскости всегда перпен. фронтали данной плоскости. Угол между линией ската и плоскостью это угол наклона на которой лежит линия ската к . линия наибольшего наклона всегда перпен. к профильной прямой данной плоскости. Если одна из сторон. -горизонталь, -фронталь, - профильная. Сохраниться прямой угол

8.Параллельность на комплексном чертеже: 2-х прямых, прямой и плоскости, 2-х плоскостей.

Одноименные проекции параллельных прямых параллельны между собой (рис. 53, а и б)

Прямая и плоскость параллельны, если их одноименные проекции параллельны между собой (рис. 104, а и б).

Если одноименные проекции плоскостей параллельны, то и плоскости параллельны (рис. 108, а и б). Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. 

9.Пересечение прямой и плоскости, пересечение 2-х плоскостей

Алгоритм построения точки пересечения прямой с плоскостью:

1. Заключить прямую в плоскость частного положения.

2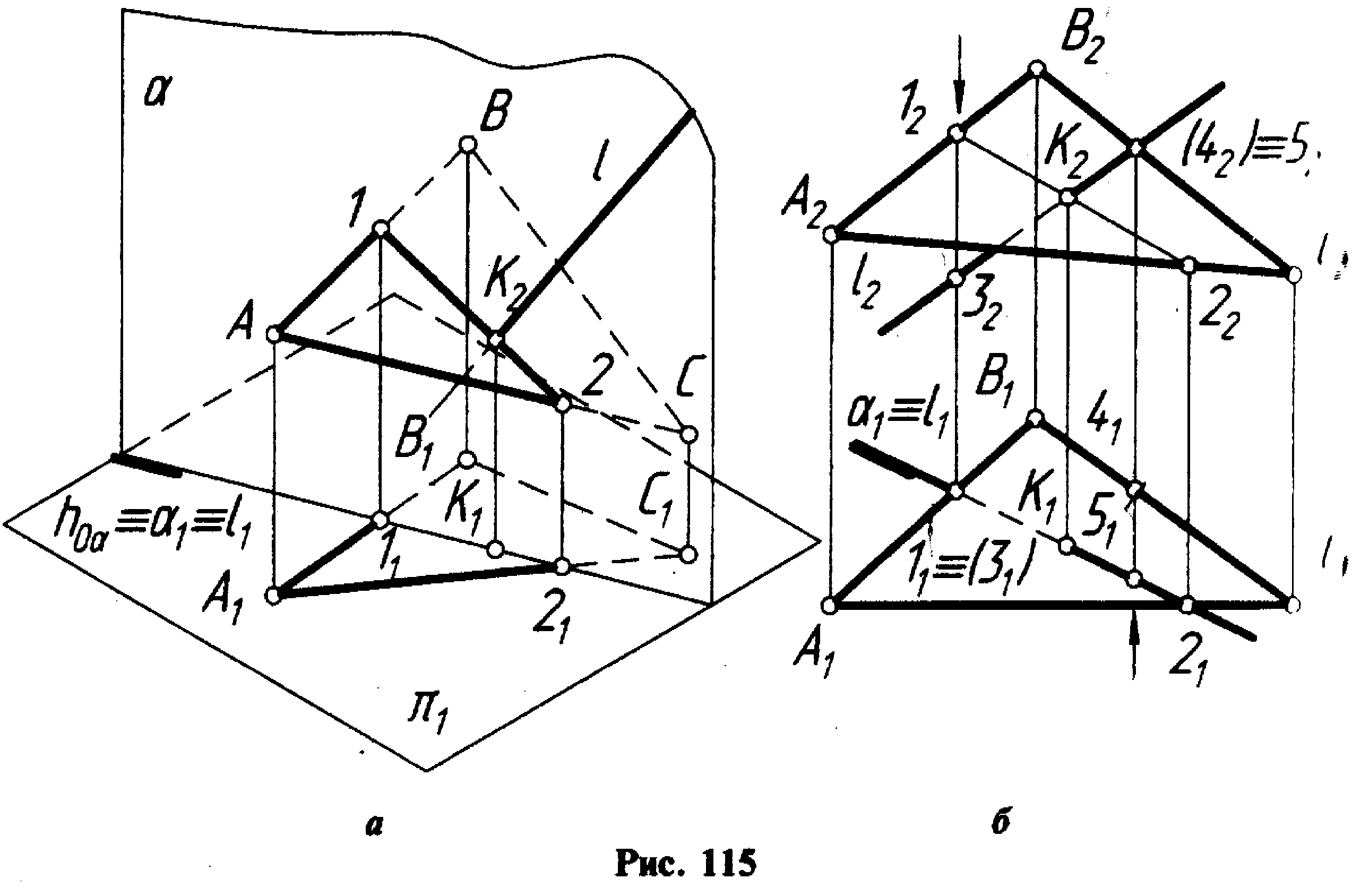.Построить линию пересечения заданной плоскости с плоскостью частного положения.

3. Определить точку пересечения заданной прямой с линией пересечения плоскостей.

Строим плоскость частного положения , совпадающую с прямой l. Прямая и плоскость на пересекаются в точкахи. По линиям связи находим эти точки на. Линиябудет искомой линией пересечения плоскостиABC с проецирующей плоскостью . Теперь проведя линию связи от точки до линии, мы получим точку, которая и будет являться искомой точкой пересечения плоскости АВС с прямойl.

Видимость объектов определяем с помощью конкурирующих точек 13, и 45

Построение линии пересечения 2-х плоскостей.

Через ВС проводим вспомогательную секущую плоскость . ВС пересекается с в точках 1 и 2. На проекциинаходим точку К – пересечение 2-х линийи.

В плоскости строим вспомогательную секущую плоскость , которая совпадает с . Аналогично находим точку пересеченияи. Это точкаL.

Линия KL и будет истинной линией пересечения и