Основные определения

Будем рассматривать унимодальные отображения , отображающие отрезок [0,1] на себя, с положением равновесия в точке А. Функция монотонно возрастает на отрезке [0, D], при этом , достигает максимального значения и затем монотонно убывает. Примером такой функции может служить «двухзонное отображение», треугольное отображение (рис.4, 5).

Положение равновесия A разбивает отрезок [0, 1] на две области: [0, A] и [A, 1]. Эти части неравноправны. В правой части траектория не может находиться два такта подряд; она служит своего рода "отражателем", фактически задавая начальные значения для движения траектории по левой части функции, а в левой части траектория может находиться произвольное число тактов.

Множество отражает специфику ОУО – показывает какое количество тактов будет находить траектория в области [0, A], определяет расстояния между максимумами внутри траектории. Оно обладает очевидным свойством: для любого натурального числа существует окрестность нуля такая, что при A_n-1< имеет ( ) ровно n тактов и затем перейдет в правую область ( ). Существует широкий класс функций, для которых может быть выбран сценарий, приводящий к тому, что в большинстве случаев множество определяет характер траекторий, в том числе длину цикла.

В ряде случаев, для практических задач исследования возможных динамических режимов в дискретном отображении оказывается достаточным использования множества . В частности в случае, когда степень достоверности (биологической) информации позволяет анализировать лишь временные интервалы между максимумами численности [3-5].

Для более детального изучения свойств рассматриваемых отображений введём две вспомогательные конструкции – линию возврата (ЛВ) и отображение за положение равновесия (ОПР).

Определение. ОПР определяется как отображение отрезка [A, 1] на себя, при котором каждому значению X из этого отрезка ставится в соответствии значение Y при первом возвращении траектории за положение равновесия.

Новое отображение можно исследовать обычными методами (поиск стационарных точек, n-кратное отображение и т.д). Соответствующим линейным преобразованием отрезок [A, 1] можно привести к отрезку [0, 1].

Кроме ОПР, определим ЛВn – линии возврата n-го порядка.

Определение. ЛВ n-го порядка (ЛВn) для отображения F называется кривая в прямоугольнике A X^t 1; 0 X^t+1 A, являющаяся графиком функции F_c⁽ⁿ⁾(X^t+1) , которая отображает отрезок 0 X^t+1 A на отрезок A X^t 1 по описанному ниже алгоритму.

Алгоритм построения ЛВn. Через любое значения X^t+1 из отрезка 0 X^t+1 A в прямоугольнике A X^t 1; 0 X^t+1 A проведем горизонтальную линию. Ее пересечение с графиком функции F(.) дает начальные условия для построения соответствующей траектории. Построим ее с помощью алгоритма создания лестницы Ламерея. При n-ом возврате за положение равновесия, согласно этому алгоритму, от биссектрисы угла между осью абсцисс и осью ординат опускаем соответствующую вертикальную линию. Точка пересечения этой линии с тестирующей горизонтальной линией принадлежит ЛВn, с координатами (X^t, X^t+1).

Тем самым в указанном выше прямоугольнике каждому значению X^t+1 соотнесено значение X^t, т.е. задана функция X^t = F_c⁽ⁿ⁾(X^t+1). Примеры графиков этой функции представлены на рис. 3 и 4. Точки пересечения ЛВn с графиком исходной функции F задают периодические траектории. При этом с помощью ЛВn можно отыскать все периодические траектории с периодом, меньшим или равным n.

Утверждение. Периодическая траектория устойчива, если включает в себя точку пересечения графика отображения F(X^t) с графиком функции F_c⁽ⁿ⁾(X^t+1) и если в этой точке существуют соответствующие производные и для них выполнено условие .

Доказательство проводится методом сжатых отображений [4].

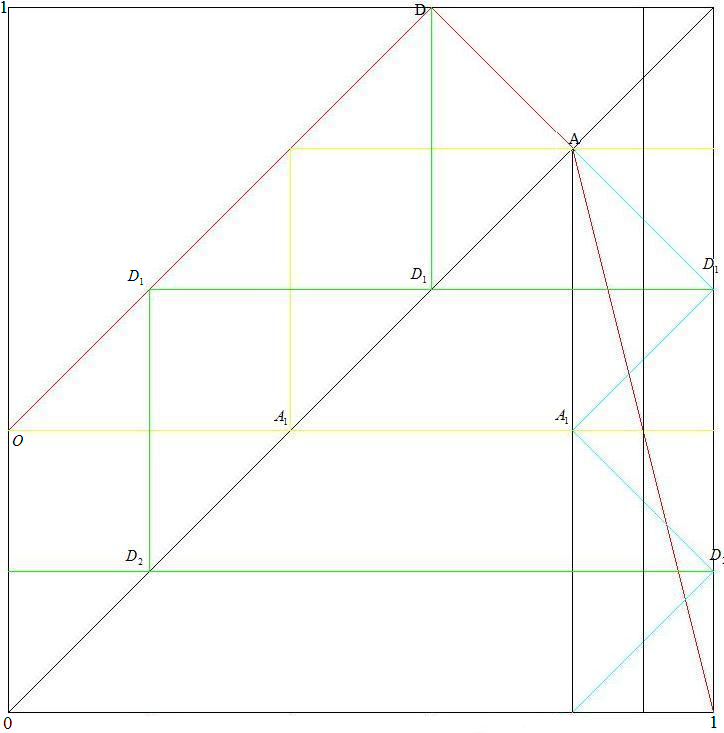
Рис.4. Двухзонное дискретное отображение (ДДО) OD1DA1 и его линия ЛВ1 AD1A1D2.

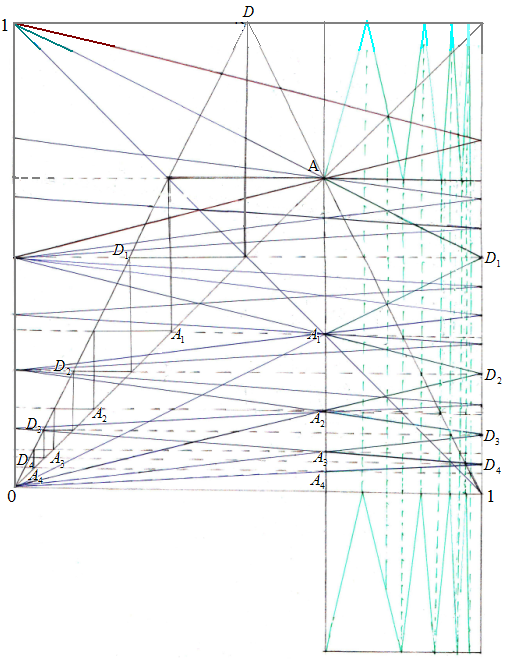
Рис.5. Треугольное отображение, его линия ЛВ1 AD1A1D2A2D3A3D4A4 и ОПР (вынесенный квадрат в правом нижнем углу или правый верхний угол), также n – кратные треугольные отображения, повёрнутые на 90 град.

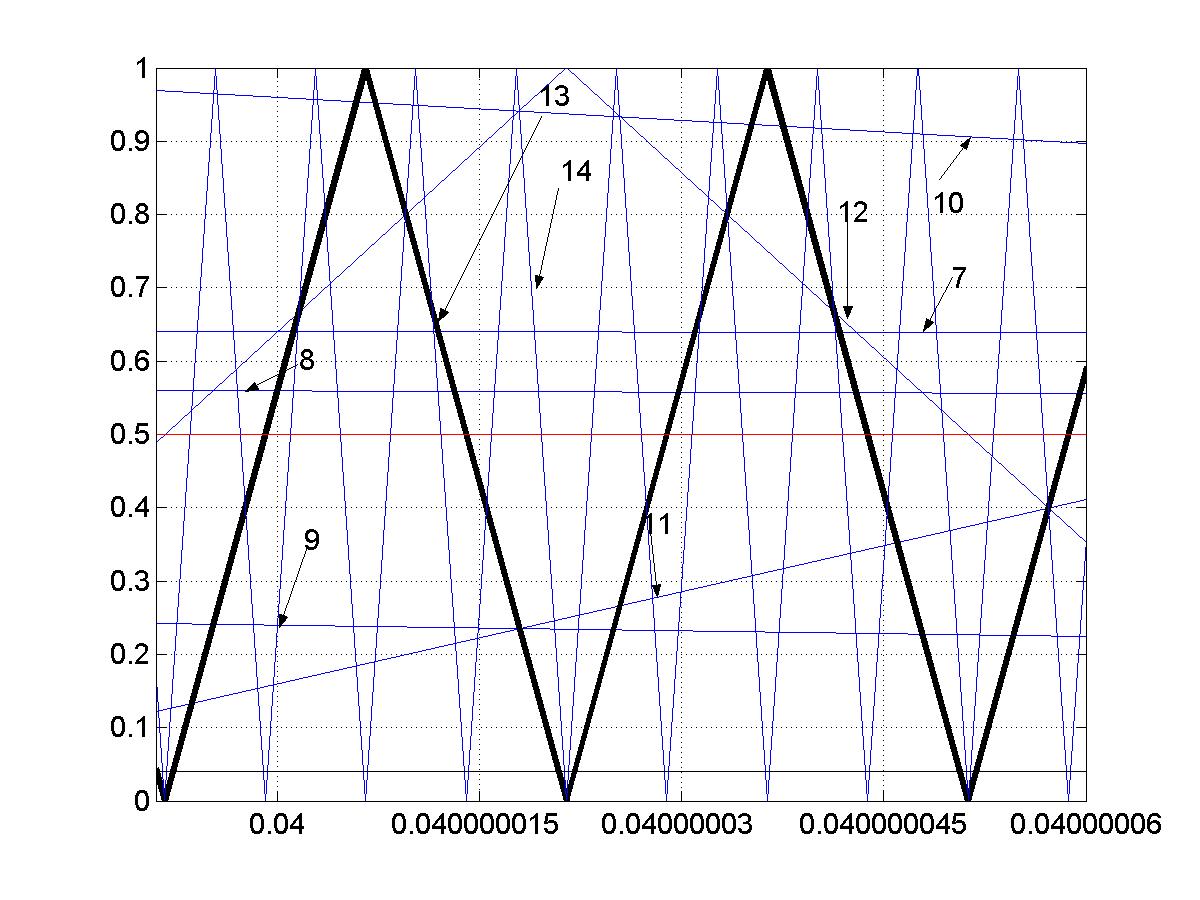
Рис.6а. Линии возврата с 7 по 14 для ДДО.

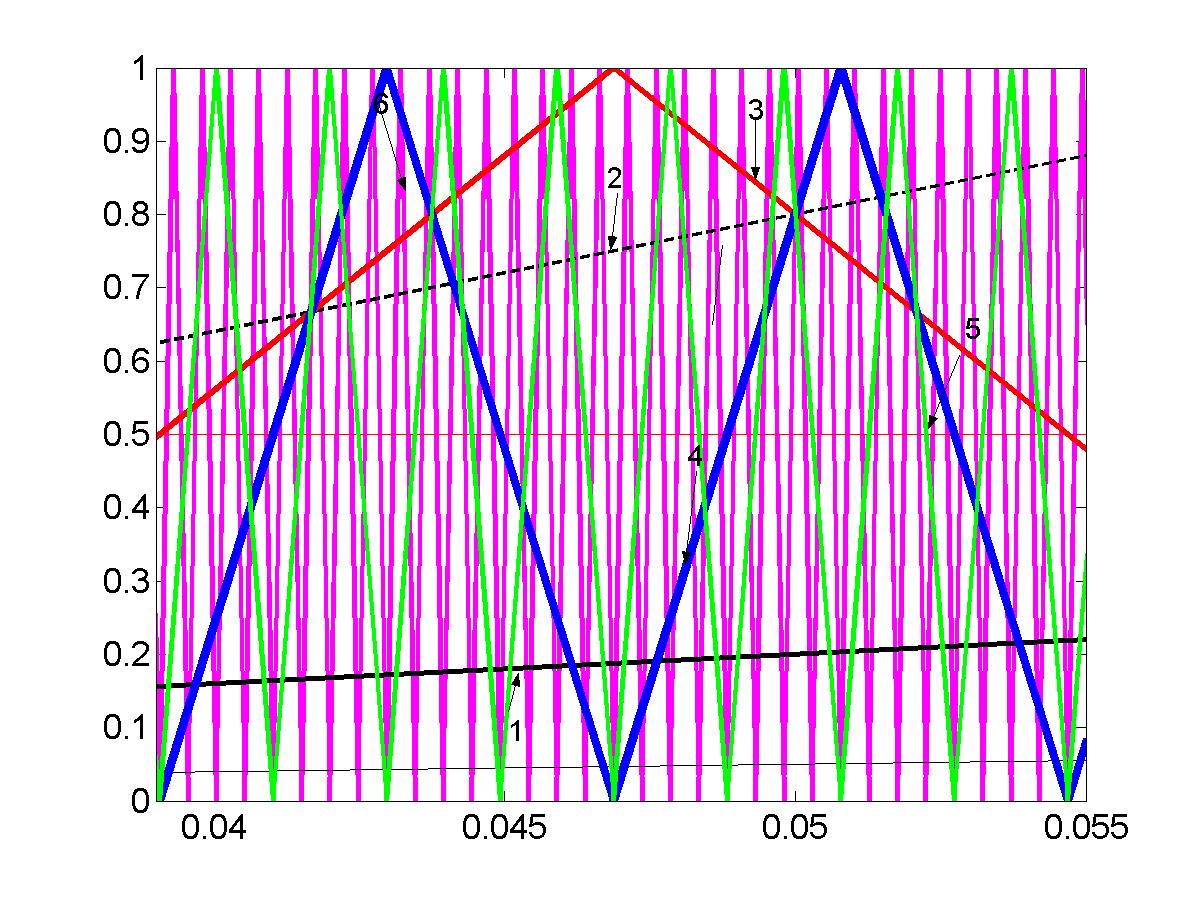
Рис.6б. Линии возврата с 1 по 6 для ДДО.

Рис.7. Треугольное 1, 2, 3-кратное отображение и его повороты на 90, 180, 270 град.