1.3. Теорія симетрованої двофазної ам при несиметричному її живленні

А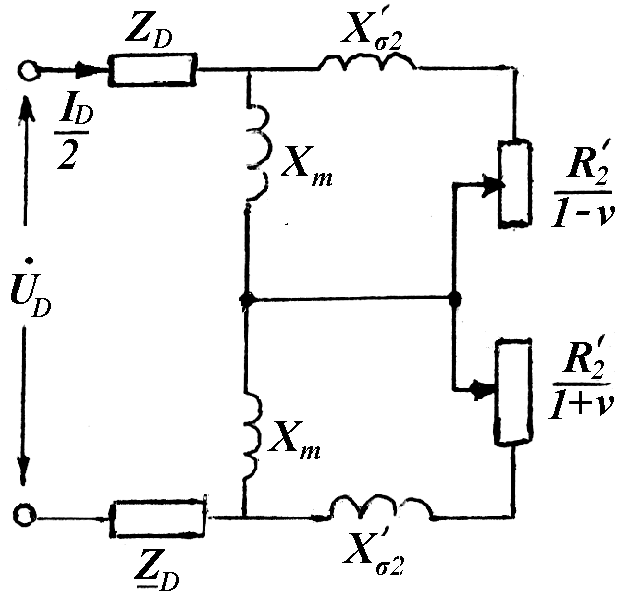 наліз симетрованої двофазної АМ при несиметричному її живленні можна здійс­нити методом обертових потоків (НС), використовуючи вирази (1.13), (1.14) і отримати для розрахунків заступну схему (рис.1.9).

Тільки тут необхідно враховувати, що НС (струм), який утворює відповідні складові – П, ЗВ, визначається половинним струмом фази. На основі цієї схеми можна обчислити всі необхідні показники і характеристики.

Рис.1.9. Заступна схема фази симетрованої двофазної АМ

Але в нашій літературі найчастіше користуються в такому випадку методом симетричних складових, який детально наводиться нижче.

Згідно з цим методом розрахунку, несиметрична двофазна система реальних чи зведених напруг, НС, або струмів, прикладена до симетрованої чи незведеної псевдо-симетричної двофазної АМ розкладаються на напруги, НС чи струми прямої послідовності та зворотної послідовності

(1.16)

г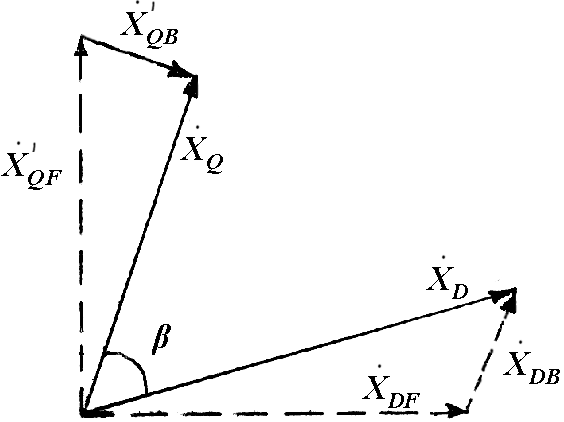 рафічно це розкладення показано на рис. 1.10.

Якщо врахувати , що для симетричних складових

, (1.17)

то з (1.16) можна визначити симетричні складові через їх несиметричні фазні величини

(1.18)

Рис.1.10. Розкладання зведеної несиметричної двофазної системи на їх симетричні складові

Використовуючи цей метод розрахунку для двофазної несиметрованої псевдо-симетричної АМ при двофазному її живленні несиметричною двофазною системою напруг можемо записати

(1.19)

у цих рівняннях симетричні складові напруг фаз є подані як спади напруг від відповідних струмів симетричних складових на відповідних опорах заступних cхем для цих же складових

(1.20)

де – повні опори заступної схеми фази D для прямої F і зворотньої В послідовностей (див. рис.1.11); – повні незведені опори заступної схеми фази Q для прямої F та зворотної В послідовностей. Заступні схеми фази Q включають такі ж опори ротора та 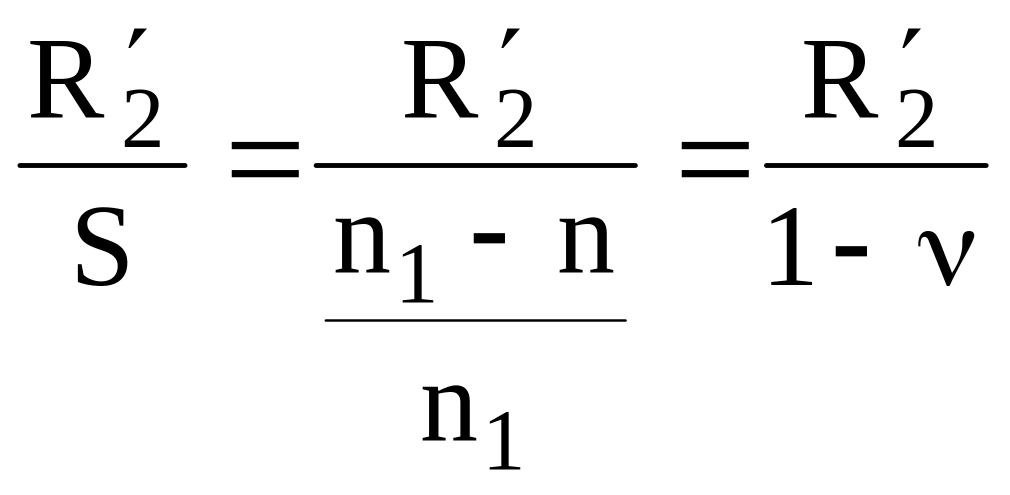– для прямої послідовності та – для зворотної послідовності, так ж опори вітки намагнічування і крім цього – замість повних опорів фази D – повні незведені опори фази Q, які звичайно включають крім опору фази статора ще величини фазо-зсувного опору .

. (1.21)

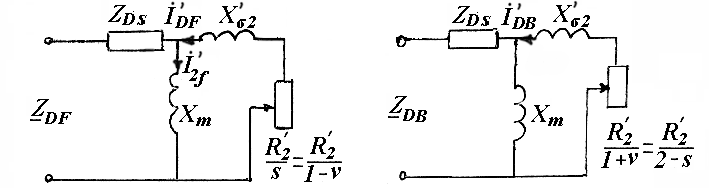
а) б)

Рис.1.11. Заступні схеми фази D для прямої F (а) та зворотної В (б) послідовностей

При цьому такі ж опори ротора – та – для прямої послідовності та 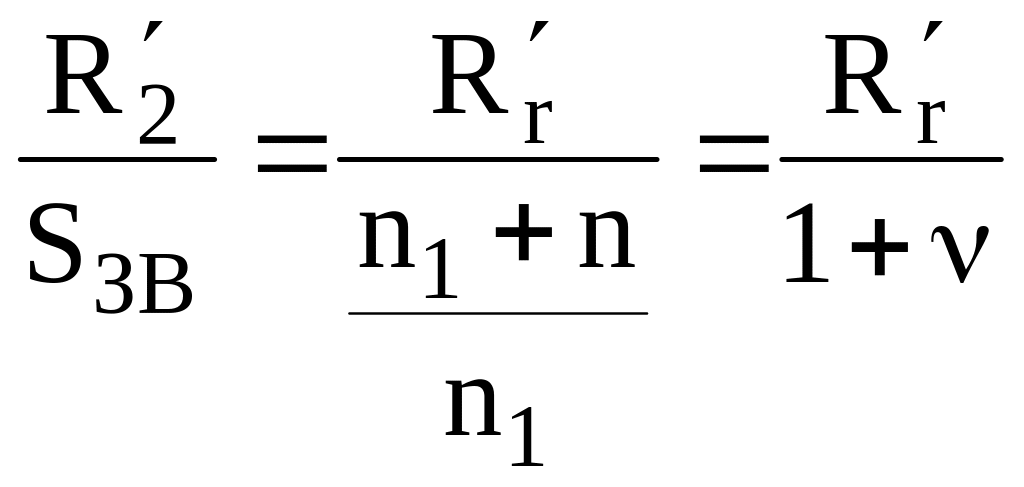– для зворотної послідовності, такі ж опори вітки намагнічування і крім цього – замість повних опорів фази D – повні незведені опори фази Q, які звичайно включають, крім опорів фази статора Q – Z_QS, ще величини фазо-зсувного опору Z_ф = R_ф – jx_ф

Z_Q = R_QS + Z_ф.

При цьому вважається, що в обмотках ротора протікають струми прямої послідов­ності з частотою які взаємодіючи з результуючим потоком Ф_F прямої послідовності, утворюють рушійний електромагнітний момент

(1.22)

та струми ротора зворотної послідовності що є в режимі проти-вмикання, з частотою які, взаємоді­ючи з результуючим потоком Ф_в зворотної послідовності, утворюють гальмівний момент

. (1.23)

Звичайно при розрахунку двофазної машини рівняння (1.19) використовують для визначення струмів, а за ними і моментів, вважаючи відомими несиметричні напруги та опори заступних схем для заданого ковзання або частоти обертання ротора .

Але цю систему рівнянь при використанні незведених струмів псевдосиметричної машини розв’язати не можна. Тому, використовуючи рівняння (1.15) і (1.17) замінимо незведені струми симетричних складових фази зведеними струмами симетричних складових фази D

. (1.24)

Із врахуванням цих співвідношень з (1.19) отримуємо струми симетричних складових

(1.25)

Знаючи ці струми, необхідно обчислити електромагнітний момент машини М, як суму моментів від прямої М_F та зворотної М_В послідовностей, вважаючи обмотки машини симетровані

= , (1.26)

де – електромагнітна потужність машини прямої послідовності;

(1.27)

– результуючий активний опір паралельного з’єднання віток намагнічування і ротора заступної схеми фази прямої послідовності,

– електромагнітна потужність машини зворотної послідовності;

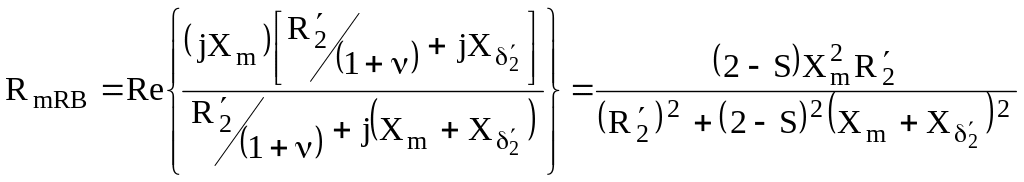(1.28)

– результуючий активний опір паралельного з’єднання віток намагні­чування і ротора заступної схеми фази зворотної послідовності.

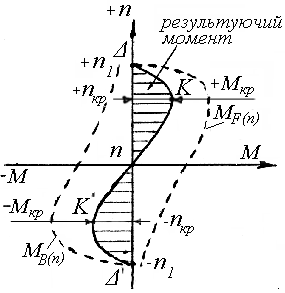
Задаючись рядом значень ковзань "s" чи частот обертання ротора, розраховуємо залежності M_F(s) та M_B(s) і додаючи їх, отримуємо меха­нічну характеристику машини для заданого ступеня несиметричності напруг, наприклад Для цієї ж машини, але при більшій несиметричності напруг рушійний момент зменшиться, а гальмівний – зросте і результуючий момент машини – зменшиться (див. рис.1.12).

Важливим показником роботи двофазної АМ є пусковий момент. Його визначають із (1.26), пам’ятаючи, що тоді s_F =s_B =1 при  = 0,

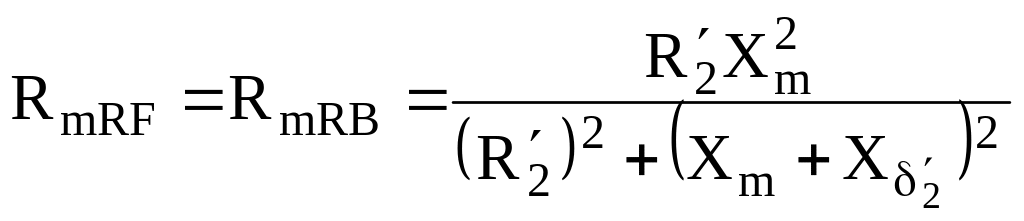, (1.29)

а величини струмів можна визначити із виразів, аналогічних до виразів (1.13), (1.14), для НС прийнявши  = 90 та замінивши в них FI_F, F_ЗВI_B та індекс N  Q

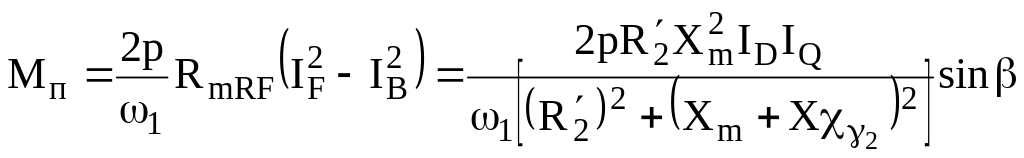. (1.30)

З цього співвідношення робимо висновок, що при заданому струмі І_D фази D двофазної псевдо-симетричної машини при несиметричному її живленні, величина її пускового моменту визнача­ється добутком "I_Q sin", де  = – часова фаза зміщення струму відносно струму .

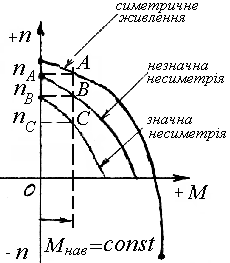
Рис.1.12. Механічні характеристики двофазної АМ при різних ступенях несиметричності напруг її живлення

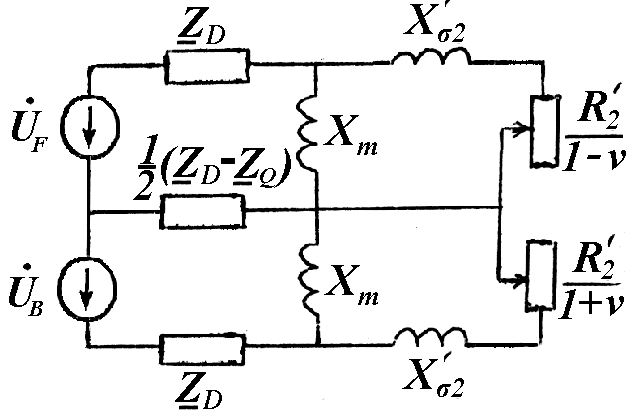
На основі рівнянь (1.25) та (1.18) можна скласти заступну схему псевдо-симетричної двофазної асинхронної машини при несиметричному її живленні, яка наведена на рис.1.13.

Ця схема АМ може бути використана для її аналізу при увімкненій в мережу тільки одній фазі статора D. Тоді U_Q  0, Z_Q   і для цього випадку заступна схема АМ перетворюється в схему рис.1.12, а рушійний електромагнітний момент машини визначається за (1.26) та (1.18)

Рис.1.13. Заступна схема псевдо-симетричної двофазної АМ при несиметричному її живленні

, (1.31)

де

При однофазному живленні двофазної АМ її пусковий момент

(1.32)

бо при  = 0, як вже згадувалось раніше, Механічна харак­теристика такої АМ наведена на рис.1.14.

Рис.1.14. Механічна характеристика АМ при увімкненій одній обмотці статора

Як видно з графіка цієї характеристики, машина не маючи пускового моменту, після того як її розігнати за рахунок стороннього моменту в будь-якому напрямку до частоти та завантажуючи моментом то вона може працювати на ділянці характеристики АК при додатній частоті обертання з додатнім моментом навантаження або на ділянці характеристики А'К' при від’ємній частоті обертання ротора, розвиваючи від’ємний електромагнітний момент.

Для утворення пускового моменту в такій машині використовують допоміжну пус­ко­ву фазу Q, яка разом з основною фазою D утворює двофазну псевдо-симетричну обмотку, наприклад за схемою рис.1.15, а величину фазо-зсувного опору Z_ф вибирають таким чином, щоби при пуску s = 1, ( = 0) результуюче поле машини було коловим.