19. Энергия магнитного поля электрического тока.

Рассмотрим проводник с током, находящийся в неферромагнитной среде.

И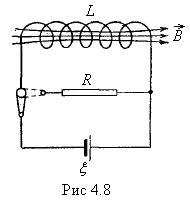 звестно, что при возрастании электрического тока в контуре возникает ЭДС самоиндукции, которая препятствует нарастанию тока, в этом случае , согласно закону Ома, ток в цепи равен:

,

где – ЭДС источника; - ЭДС самоиндукции, R - сопротивление.

Объемная плотность энергии магнитного поля называется энергия этого поля, отнесенная к его объему:

- если среда изотропная, линейная и неферромагнитная.

Энергия , локализованная во всем объеме магнитного поля равна:

. .

Если поле в данной точке пространства создано несколькими контурами с током,

то энергия результирующего магнитного поля равна: ,

где - потокосцепление к-того контура, - сила тока в к-том контуре,

при этом

- равно потокосцеплению самоиндукции (магнитному потоку самоиндукции) к-того контура плюс магнитный поток взаимоиндукции к0того контура с остальными.

Поэтому энергия магнитного поля равна

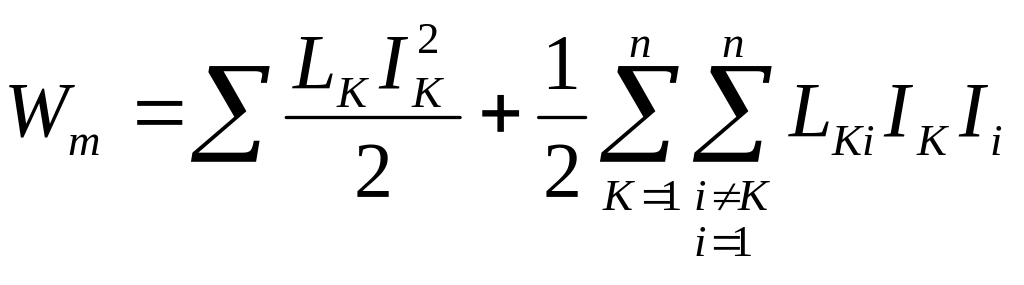
– взаимная индуктивность к-того и i- того контуров с токами и .

4.7.Закон сохранения энергии в неферромагнитной среде

Энергия магнитного поля, создаваемого какой-либо системой тел (проводящих контуров с токами) изменяется, если контуры с токами перемещаются, или, если изменяются токи в них.

При этом совершают работу внешние силы, приложенные к телам системы, источники электрической энергии, включенные в цепи токов.

Если температура системы постоянна, и плотность среды не меняется, то закон сохранения энергии можно записать в виде:

,

здесь - работа внешних сил в рассматриваемом процессе, - работа источников электрической энергии, - изменение энергии магнитного поля, - изменение кинетической энергии тел системы, - теплота Джоуля-Ленца.

Если тела системы перемещаются очень медленно (квазистатически), то можно пренебречь изменением кинетической энергии системы, =0, и можно считать , где - работа сил, действующих на тела системы в магнитном поле. Это пондемоторные силы. Тогда закон сохранения энергии примет вид:

.

Если система содержит n проводящих контуров с токами, работа источников электрической энергии за малый промежуток времени dt равна:

,

где – алгебраическая сумма ЭДС всех источников электрической энергии, включенных в -тый контур, – сила тока в этом контуре.

Рассмотрим некоторые примеры.

1. Неподвижный контур с током.

а) Если ток в контуре остается постоянным, то энергия магнитного поля не изменяется, , а пондемоторные силы не совершают работы: , поэтому

- вся работа источника электрической энергии преобразуется в контуре в тепло Джоуля-Ленца.

б) Пусть ток в контуре растет от 0 до . Работа пондемоторных сил равна нулю и работа источника электрической энергии в контуре расходуется на изменение знергии магнитного поля и на выделение тепла Джоуля-Ленца: , или , где - ЭДС источника, R - сопротивление, L – индуктивность контура, I -сила тока в нем.

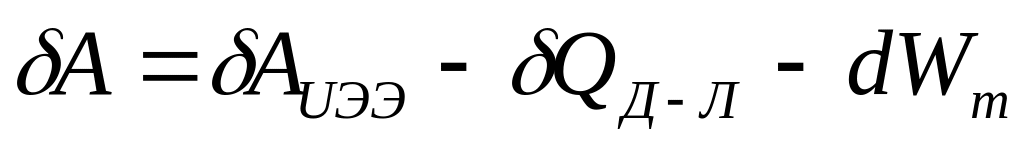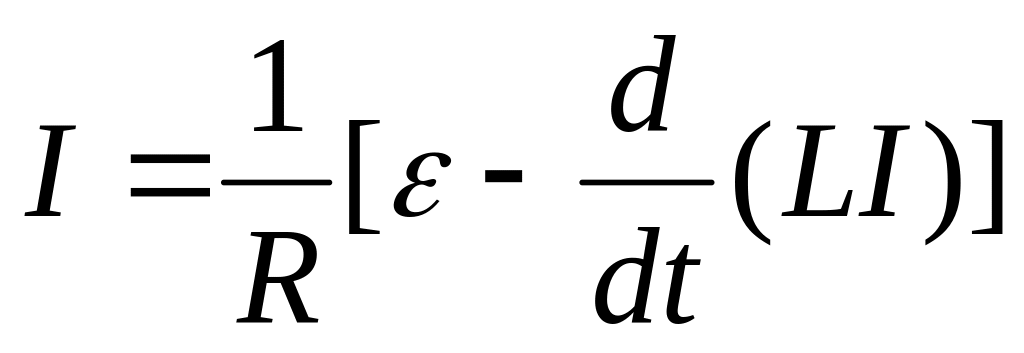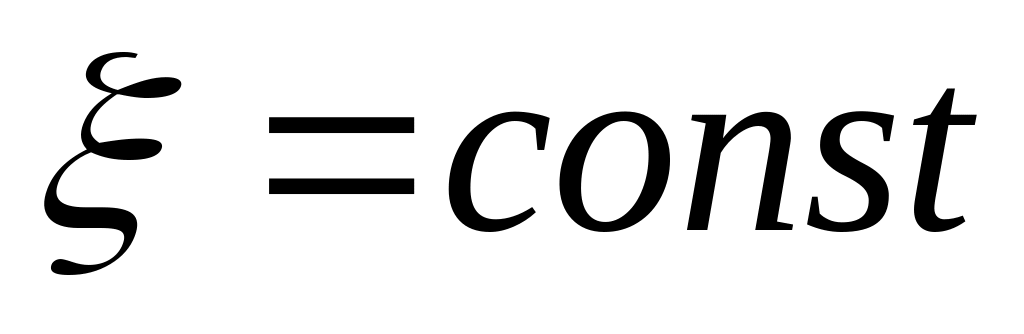2. Работа пондемоторных сил при очень медленной деформации контура с током. Закон сохранения энергии имеет вид: . Сила тока I в контуре изменяется под влиянием ЭДС самоиндукции , где – ЭДС источника постоянного тока в контуре, тогда работа источников электрической энергии

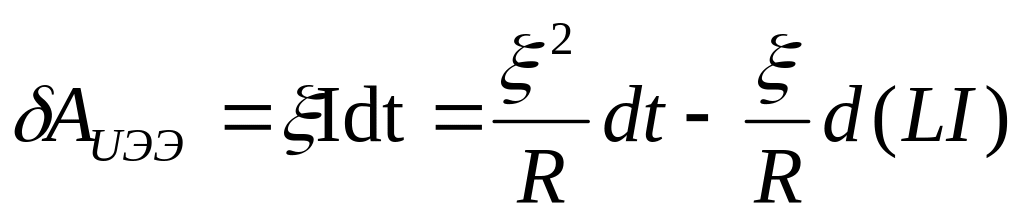
При очень медленной деформации контура ЭДС самоиндукции мала по сравнению с , поэтому теплота, выделяемая по закону Джоуля-_Ленца, равна , и .

Таким образом, элементарная работа пондемоторных сил . Полная работа пондемоторных сил 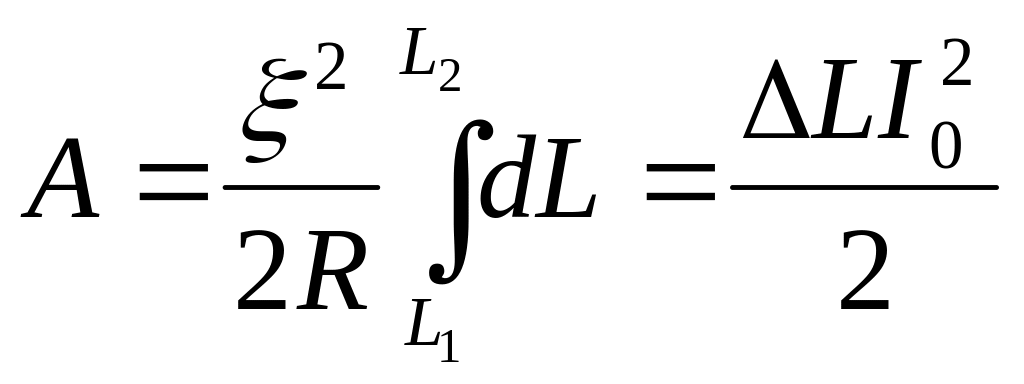, где – изменение индуктивности контура при его деформации, – постоянный ток в контуре до и после его деформации.