3.3. Определение касательных напряжений от кручения

Кручение конструкции, в результате которого в её нормальном сечении возникают только касательные напряжения, называется свободным. Такое напряжённо - деформированное состояние конструкция испытывает вдали от заделки крыла, от его крепления к фюзеляжу. Эта задача аналогична задаче определения касательных напряжений (или погонных касательных усилий) от сдвига. Например, в случае трёхзамкнутого сечения разрезаем все панели крыла, за исключением последней, по образующей (идя по хорде крыла от носка).

Распишем погонные касательные потоки по панелям сечения (по аналогии с расчётом на сдвиг, только здесь в потоках будет отсутствовать поток в открытом контуре .

Для определения неизвестных погонных замыкающих потоков составляем канонические уравнения:

.

Коэффициенты соответственно равны коэффициентам канонических уравнений для сдвига.

Через и обозначены соответственно относительные углы закручивания сечения и площади контуров: - площадь контура , - площадь контура и - площадь контура . Четвёртым уравнением для определения четырёх неизвестных , и будет уравнение равновесия

.

В правую часть уравнения равновесия входит координата центра жёсткости се- чения .

Координата центра жёсткости сечения определится выражением

.

В этой формуле первые слагаемые в скобках – произведения замыкающих интенсивностей на площади соответствующего контура “в свету”. Расчёт сводится в табл. 9.

Таблица 9

1	2	3	4	5	6
Номер панели	qoi	Si		2i=iSi	2qoii
	Н/м	м	м	м2	Н*м
1
2
3
...
n-1
n

Пояснения к таблице:

Здесь величины в столбцах 2 и 3 берутся из расчёта на сдвиг.

Величина - длина перпендикуляра, опущенного из начала координат, расположенного в передней точке профиля на касательную к обводу рассматриваемой панели в её средней точке.

Решение уравнения даёт погонные замыкающие касательные потоки . Зная их, определяют погонные касательные усилия в панелях контуров, а далее

определяют касательные напряжения:

.

Последним этапом расчёта будет суммирование погонных касательных потоков от сдвига и кручения, определение касательных напряжений в панелях. Расчёт удобно свести в табл. 10.

Таблица 10

Номер панели	qiСДВ	qiКР	qiСУМ			КР	
	Н/м	Н/м	Н/м	м	Н/м2	Н/м2	--
1
2
3
...
n-1
n

Вычисляются величины касательных критических напряжений и запас прочности

,

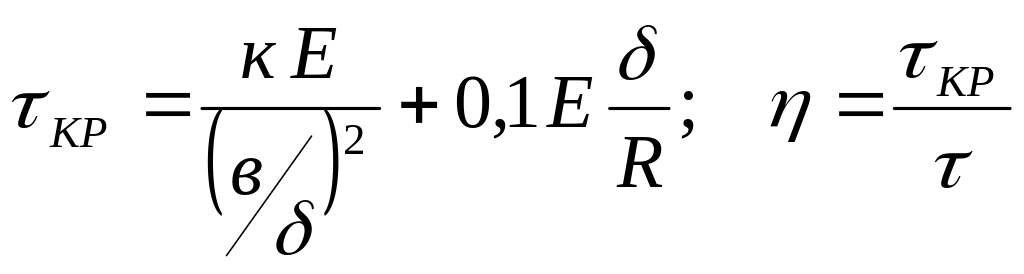где - коэффициент, учитывающий опирание панели ( для свободно

опёртых краёв и для защемлённых краёв ).

- расстояние между стрингерами.

- радиус кривизны панели.

- модуль упругости рода.