3.2. Определение касательных напряжений от сдвига

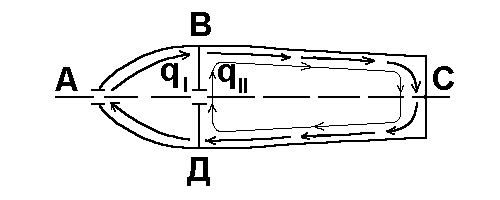Расчёт начинается с вычерчивания сечения и выбора основной системы конструкции ( делаются разрезы по хорде от носка крыла, которые превращают сечения в открытый контур (рис. 16)).

Рис. 16

В местах разрезов прикладываются замыкающие интенсивности и (погонные касательные усилия ), уравновешивающие поперечную силу , приложенную в центре жёсткости крыла. Поперечная сила, обусловливающая изгибающий момент, вызывает так же сдвиг и кручение сечения. Понятие центра жёсткости ( центр жёсткости сечения – точка, в которой приложенная поперечная сила вызывает чистый сдвиг ) даёт возможность разделить нагружение на:

1) сдвиг силой ;

2) кручение моментом .

При этом для расчёта на сдвиг не требуется знания положения центра жёсткости, т.к. только крутящие моменты зависят от его координат.

После выбора основной системы нумеруются все стрингеры и панели, причём стрингер и предшествующая ему панель имеют один и тот же номер

( например, панель со стрингерами 1 и 2 будет иметь №2, а панель со стрингерами и 1 будет нумероваться номером 1 и будет замыкающей ).

Расписываются погонные касательные усилия в панелях контура:

,

где - касательные потоки в открытом контуре;

- замыкающие погонные потоки ( принимает значения и ).

Погонная касательная сила в любой панели при сдвиге замкнутого контура равна погонной касательной силе в том же незамкнутом контуре плюс замыкающие погонные силы ( ), причём каждая замыкающая сила добавляется только на тех панелях контура, которые являются элементом, замыкающим его. Например, поток замыкает весь контур , а поток замыкает только хвостовую часть .

Замыкающие погонные потоки определяются из системы канонических уравнений для произвольного многосвязанного контура из контуров:

где .

Здесь - длина панели; - модуль упругости рода; - толщина панели;

- погонная сила в панели, возникающая в незамкнутом контуре.

Для двухсвязного контура канонические уравнения имеют вид

,

.

.

Здесь - перерезывающая сила в сечении; - статический момент относительно оси всех площадей редуцированного сечения рассматриваемой части конструкции; - момент инерции приведённого сечения относительно главной центральной оси,

где (суммирование ведётся по контуру , замыкаемому потоком ).

(суммирование ведётся по контуру , замыкаемому потоком ).

.

Вообще, коэффициенты , у которых первый индекс равен единице, образуются из суммирования величин, относящихся ко всему контуру .

И окончательно, коэффициент :

при определяется формулой: ;

при определяется формулой: .

Суммы распространяются на те участки, где одновременно действуют погонные касательные силы и .

Таким образом, для составления канонических уравнений, достаточно расписать погонные касательные силы по контуру, как это сделано на рис. 16 и, вычислив суммирующиеся и , произвести их сложение в пределах одновременного действия двух сил и .

Из канонических уравнений находят замыкающие погонные касательные потоки , а следовательно, и .

Зная замыкающие погонные касательные усилия, определяют касательные напряжения в консолях и запас прочности:

и .

Делаются выводы о работе обшивки в панелях.

Расчёты удобно свести в табл. 8.

Таблица 8

1	2	3	4	5	6	7	8	9	10	11	12	13
Номер элемента	yi	Fiпр	Sпр	Номер панели	x-1 Siпр	qок	Si	i	iпр	Si Gi iпр	qокSi Gi iпр	qiсдв
	м	м2	м3		м3		м	---	м	м2/Н	м
1				1
2				2
3				3
...				...
n-1				n-1
n				n

Пояснения к таблице:

В столбцах 2 и 3 значения величин берутся из расчёта на изгиб.

Приращение статического момента на данном элементе (столбец 4) в каждой строке равно произведению величин столбцов 2 и 3.

Панели имеют номер последующего элемента при обходе контура по часовой стрелке.

Статический момент участка контура (столбец 6) от начала отсчёта до рассматриваемой панели. Это – нарастающая сумма величин столбца 4 (сверху или снизу столбца – безразлично). . Здесь - момент инерции всего сечения крыла, взятый из расчёта на изгиб.

(столбец 8) – длина рассматриваемой панели; берётся замером с чертежа сечения.

Редукционные коэффициенты , учитывающие неодинаковые условия работы на сдвиг различных панелей (находятся по таблицам “Справочника авиаконструктора”).

Приведённая толщина обшивки вычисляется по формуле .

Столбец 13 – суммарная интенсивность сдвига – вычисляется по формуле . Коэффициенты канонических уравнений равны суммам столб- ца 11 по тем участкам, где одновременно действуют касательные потоки с но- мерами, принадлежащими коэффициенту в качестве индексов. Свободный член уравнения – сумма столбца 12 по соответствующим участкам контура сечения.