Смешивание углеродных материалов
2.4.1 Статистический характер процесса смешивания
Смешиванием называется процесс, в результате которого первоначально находящиеся раздельно компоненты после равномерного распределения каждого из них в смешиваемом объеме материала образуют однородную смесь.
Равномерность смешивания исходных компонентов (фракции кокса), а также сухой шихты с жидким связующим при получении углеродных материалов является важнейшим условием получения качественного конечного продукта (искусственного графита).
Смешивание сыпучих компонентов является сложным процессом, зависящим от ряда условий, одни из которых действуют постоянно и оказывают непрерывное влияние на качество смешивания, а другие вызывают переменное, случайное воздействие на распределение свойств в смешиваемых объемах. К числу постоянно действующих относятся следующие факторы: конструктивная форма смесителя и основных его деталей; скорость перемещения частиц при смешивании; соотношение между содержанием компонентов в смеси; степень наполнения смесителя шихтой; кажущаяся плотность смеси; соотношение плотностей отдельных компонентов смеси; гранулометрический состав смешиваемых компонентов.
Одновременно с перечисленными выше действуют факторы, являющиеся переменными условиями смешивания, а именно: форма частиц смешиваемых порошков; колебания в гранулометрическом составе в результате истирания и сегрегации; различные отклонения в свойствах поступающих на смешивание порошков.
С точки зрения вероятности происходящих при смешивании изменений действие переменных факторов может рассматриваться как случайное. В соответствие с этим, соотношение компонентов и некоторых их свойств в различных объемах смеси должно являться для отдельных моментов процесса вероятностной величиной. В пределе смешивание должно привести к состоянию, при котором частицы любого компонента таким образом случайно распределены в смеси, что имеют равную вероятность нахождения в любом объеме смеси.
Рассматриваемая переменная представляет собой усредненную величину для значительного числа частиц, составляющих смесь. В связи с этим описание процессов, происходящих при смешивании, должно основываться на статистических методах оценки качества смешивания и распределения свойств в смеси.
Наблюдения Ластовцева А.М. и Фиалкова А.С. [6] показывают, что при смешивании порошковых материалов распределение свойств в смешиваемом объеме через некоторое время (спустя несколько минут после начала смешивания) начинает следовать закону нормального распределения Гаусса – Лапласа. Этот закон выражается следующим образом:
<
<
,
(30)
где
<
<
– частота значений свойств, попадающих
в интервал
;
– число наблюдавшихся случаев;
– стандартное отклонение наблюдаемого свойства;
– наблюдаемое значение свойства
(варианта);
–
значение свойства в условиях идеального
распределения.
Стандартное отклонение определяется по формуле:
,
(31)
где – стандартное отклонение;
– значение варианты;
– среднеарифметическое значение
изменяемого показателя в смеси;
– число наблюдений.
Стандартное отклонение, определяемое
по уравнению (31), основанное на классической
теории ошибок используется, как правило,
при очень большом числе определений
(
).
При ограниченном числе определений
используют выборочное стандартное
отклонение
.
В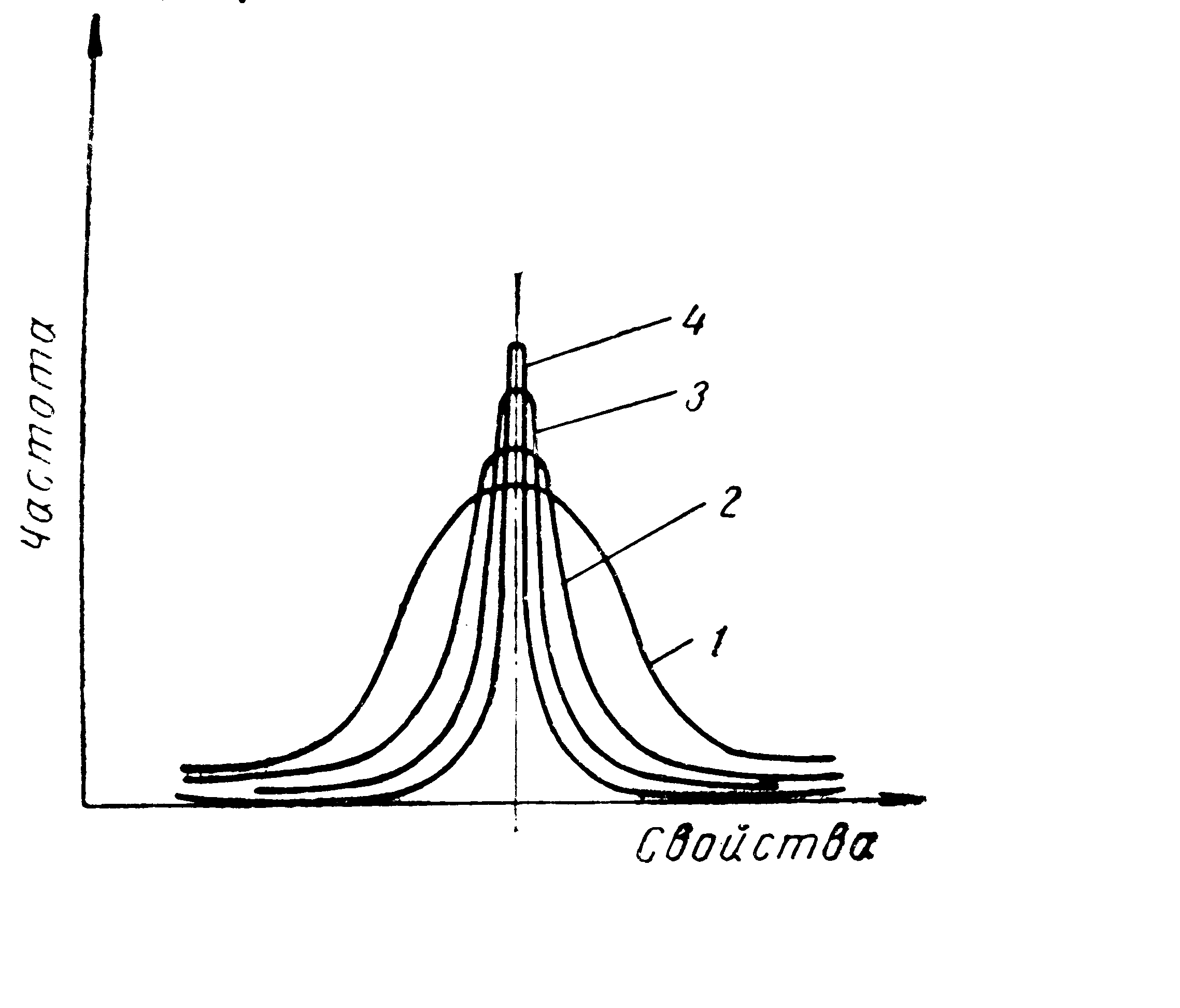
процессе смешивания происходит изменение
статистических параметров распределения.
С увеличением времени смешивания (до
определенного предела) наблюдается
уменьшение среднеквадратичного
отклонения. Указанные изменения
отражаются на виде кривой распределения
(рисунок 2.20).
1, 2, 3, 4 – кривые для последовательных промежутков времени
Рисунок 2.20 – Характер изменения кривой распределения свойств в смешиваемом объеме во времени
В процессе смешивания наблюдается вытягивание кривой по оси ординат и уменьшение ее полуширины (значение ширины кривой распределения на половине высоты пика).
Наиболее полно качество смешивания
описывает нормальное распределение
контролируемых величин. Для количественной
оценки качества смешивания распределение
компонентов и других показателей проб,
отобранных из смешиваемых объемов,
сравнивается с теоретической частотой
распределения тех же показателей по
нормальному закону [7]. Расчет ведется
по критерию Пирсона
:
,
(32)
где – число пар опытных и теоретических частот;
– опытная частота;
– теоретическая частота.
В зависимости от значения можно сделать заключение о качестве приготовления смеси. Удовлетворительными считаются смеси при значениях , больших 0,3 .
Заменяя обозначение варианты некоторого свойства ( ) на концентрацию компонента в i-той пробе и исходя из статистического характера смешивания, показатель однородности смесей можно вычислять из выражения:
,
(33)
где – выборочное стандартное отклонение;
– концентрация компонента в i-той
пробе;
– среднеарифметическое значение доли
компонента в смеси;
– общее число проб.
Ластовцев А.М. [9] рекомендует для оценки
качества смесей определять коэффициент
неоднородности
,
%:
,
(34)
где
– концентрация компонента при идеальном
распределении;
– концентрация одного из компонентов в пробах;
– число проб с концентрацией
;
– общее число проб.
Для оценки изменений стандартного отклонения в процессе смешивания может быть использован показатель интенсивности смешивания:
,
(35)
где – выборочное стандартное отклонение, определяемое по формуле (33),
– стандартное отклонение до начала
смешивания.
Стандартное отклонение до начала смешивания определяется по формуле (36):
,
(37)
где
– доля первого компонента;
– доля второго компонента.
Отношение
(39), где
– предельно достижимое или заданное
стандартное отклонение показателей
при смешивании, является оценкой
достигнутого качества смешивания по
сравнению с заданным.
Статистически более правильно показатель интенсивности смешивания может быть определен следующим образом
,
(38)
где – выборочное стандартное отклонение, определяемое по формуле (33),
– стандартное отклонение до начала смешивания.
Минимальное число проб для выполнения статистических расчетов должно быть не менее 40.
Исследование кинетики смешивания
показывает, что
изменяется по экспоненциальному закону:
,
(39)
где
– константа скорости, зависящая от
физических характеристик порошков и
конструкции смесильных машин;
– время смешивания.