
- •Лариса Кондратьєва, Ольга Тепцова алгебра Збірник контрольних і самостійних робіт
- •Передмова
- •Контрольна робота №1. Вхідне діагностичне оцінювання
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Самостійна робота №1. Числові нерівності та їх властивості
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Самостійна робота №3. Числові проміжки. Розв’язування нерівностей
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Самостійна робота №5. Функція. Властивості функції
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Самостійна робота №6. Перетворення графіків функцій
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Самостійна робота №8. Нерівності другого степеня. Розв’язування нерівностей методом інтервалів
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Контрольна робота №4. Функція. Квадратична функція. Квадратні нерівності
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Підсумкова контрольна робота за і семестр
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Самостійна робота №9. Системи рівнянь із двома невідомими
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Контрольна робота №5. Система рівнянь із двома невідомими
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Самостійна робота №11. Елементи прикладної математики
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Контрольна робота №6. Елементи прикладної математики
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Самостійна робота №12. Арифметична прогресія. Формула n-го члена арифметичної прогресії
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Самостійна робота №13. Формула суми n перших членів арифметичної прогресії
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Самостійна робота №14. Геометрична прогресія. Формула n-го члена геометричної прогресії
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Самостійна робота №15. Формула суми перших n членів геометричної прогресії. Нескінченна геометрична прогресія
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Контрольна робота №7. Арифметична та геометрична прогресії
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Самостійна робота №16. Повторення і систематизація навчального матеріалу
- •Бланк відповідей
- •Бланк відповідей
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Початковий рівень
- •Середній рівень
- •Достатній рівень
- •Високий рівень
- •Контрольна робота №8. Підсумкова контрольна робота
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
- •Частина 1
- •Частина 2
- •Бланк відповідей Частина 1
- •Частина 2
Середній рівень
9. Знайти область
визначення функції y = ![]() .
.
10. За якого значення аргументу значення функції y = 5x2 – 8x дорівнює 4?
11. Довести, що функція y = 5x3 – 2x є непарною.
12. Функція y = f(x) є спадною на множині (–; 5). Порівняти значення функції: f(–10) і f(–3); f(3) і f(4,2).
13. Знайти значення x, за яких функції y = 3 і y = x – 2 набувають однакових значень (графічно, аналітично).
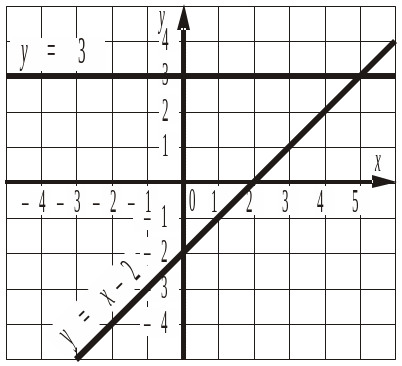
14. Побудувати
графік функції y = ![]() .
Знайти проміжки, на яких функція набуває
від’ємних значень.
.
Знайти проміжки, на яких функція набуває
від’ємних значень.
Достатній рівень
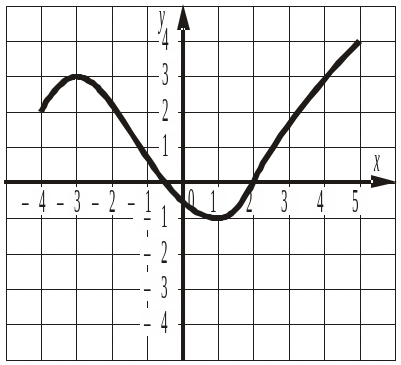
15. Для функції, заданої на проміжку [–4; 5] і графік якої зображено на рисунку, знайти:
а) нулі функції;
б) проміжки спадання функції;
в) проміжки, на яких функція набуває від’ємних значень.
16. Знайти область
визначення функції y = ![]() +
+ ![]() .
.
17. Дослідити на
парність функцію y = ![]() .
.
18. Знайти нулі функції y = x3 – 9x2 + x – 9.
19. Побудувати
графік функції
![]() Знайти множину значень функції.
Знайти множину значень функції.
Високий рівень
20. Знайти область
визначення функції y = ![]() +
+ ![]() .
.
21. Функцію
задано формулою y = x4 + 5x2 + 1.
Довести, що f![]() =
= ![]() .
.
22. Довести, що функція y = 5x + 4 зростає на проміжку (–; +).
23. Знайти значення
x, за якого значення функції
y(x) = ![]() + 2
дорівнює 1.
+ 2
дорівнює 1.
24. Побудувати
графік функції y = ![]() .
.
Самостійна робота №6. Перетворення графіків функцій
ВАРІАНТ 1
1. Графік якої функції зображено на рисунку?
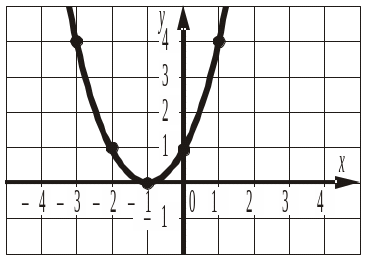
а) y = x2 + 1; б) y = x2 – 1; в) y = (x – 1)2; г) y = (x + 1)2; д) y = –x2 + 1.
2. На рисунку зображено графіки
функцій
![]() і y =
+ c.
Знайти значення c.
і y =
+ c.
Знайти значення c.
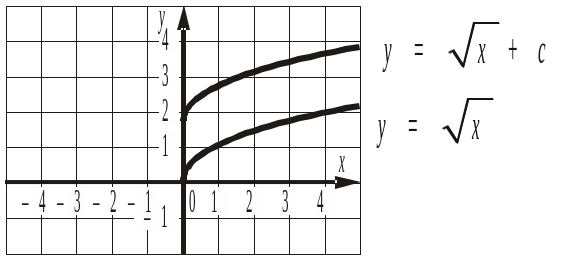
а) 1; б) 2; в) –2; г) 3; д) –3.
3. На яку відстань і в якому напрямку
необхідно перенести графік функції
y = ![]() ,
щоб отримати графік функції y =
– 5.
,
щоб отримати графік функції y =
– 5.
а) На 5 одиниць вгору; б) на 5 одиниць вниз; в) на 5 одиниць праворуч; г) на 5 одиниць ліворуч; д) на 5 одиниць вниз і ліворуч.
4. Зобразити схематично графік функції y = –х2 + 3 і знайти множину значень функції.
а) (–∞; 3]; б) [3; +∞); в) (–∞; –3]; г) [–3; +∞); д) [0; +∞).
5. Побудувати графік функції y = (x + 2)3 – 1. Знайти значення аргументу, за яких значення функції є додатними.
а) (–2; +∞); б) (–1; +∞); в) (2; +∞); г) (1; +∞); д) (0; +∞).
6. Записати формулою функцію, яка набуває однакових значень з функцією y = x2 за значень аргументу, які на 3,5 менші від відповідних значень аргументу заданої функції.
7. Скільки коренів має рівняння
![]() = (x – 1)2?
= (x – 1)2?
8*. Побудувати
графік функції y = ![]() .
.
Бланк відповідей
|
1 |
2 |
3 |
4 |
5 |
а |
|
|
|
|
|
б |
|
|
|
|
|
в |
|
|
|
|
|
г |
|
|
|
|
|
д |
|
|
|
|
|
6 |
|
|
7 |
|
ВАРІАНТ 2
1. Графік якої функції зображено на рисунку?
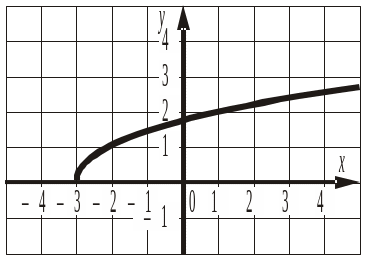
а) y = ![]() ; б) y =
; б) y = ![]() ; в) y = (x + 3)2; г) y =
; в) y = (x + 3)2; г) y = ![]() ; д) y =
; д) y = ![]() .
.
2. На рисунку зображено графіки функцій y = x2 і y = x2 + a. Знайти значення a.
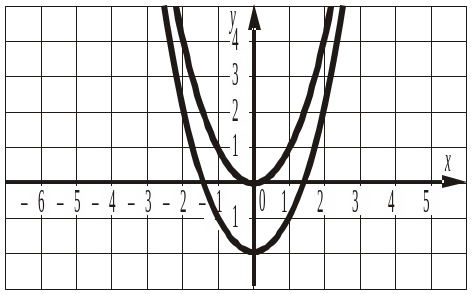
а) 1; б) 2; в) –2; г) 3; д) 0.
3. На яку відстань і в якому напрямку необхідно перенести графік функції y = x3, щоб отримати графік функції y = (x – 4)3.
а) На 4 одиниці вгору; б) на 4 одиниці вниз; в) на 4 одиниці праворуч; г) на 4 одиниці ліворуч; д) на 4 одиниці вниз і ліворуч.
4. Зобразити схематично графік функції y = –(х – 3)2 і знайти множину значень функції.
а) (–∞; 3]; б) [3; +∞); в) (–∞; 0); г) (–∞; 0]; д) (–∞; –3].
5. Побудувати графік функції y = ![]() .
Знайти значення аргументу, за яких
значення функції є від’ємними.
.
Знайти значення аргументу, за яких
значення функції є від’ємними.
а) (5; +∞); б) (1; 5); в) [1; 5); г) (–∞; 5); д) [1; 5].
6. Записати формулою функцію, яка набуває з функцією y = однакових значень за значень аргументу, які на 5,3 більші від відповідних значень аргументу заданої функції.
7. Розв’язати графічно рівняння
![]() + 3 = (x – 1)3 + 1.
+ 3 = (x – 1)3 + 1.
8*. Побудувати
графік функції y = ![]() .
.
