11.8. Рангово-бисериальный коэффициент корреляции

В тех случаях, когда одна переменная измеряется в дихотоми­ческой шкале (переменная X), а другая в ранговой шкале (пере­менная У), используется рангово-бисериальный коэффициент корреляции. Мы помним, что переменная X, измеренная в дихо­томической шкале, принимает только два значения (кода) 0 и 1. Особо подчеркнем: несмотря на то что этот коэффициент изме­няется в диапазоне от -1 до +1, его знак для интерпретации ре­зультатов не имеет значения. Это еще одно исключение из обще­го правила.

Расчет этого коэффициента производится по формуле:

(11.17)

где Х1 -- средний ранг по тем элементам переменной Y, кото­рым соответствует код (признак) 1 в переменной X;

236

Х0 -- средний ранг по тем элементам переменной Y, которым соответствует код (признак) 0 в переменной X;

N— общее количество элементов в переменной X.

Решим следующий пример с использованием рангово-бисе-риального коэффициента корреляции.

Задача 11.8. Психолог проверяет гипотезу о том, существуют ли тендерные различия в вербальных способностях.

Решение. Для решения данной задачи 15 подростков разно­го пола были проранжированы учителем литера­туры по степени выраженности вербальных спо­собностей. Полученные данные представим сразу в виде таблицы 11.11:

Таблица 11.11

№ испытуемого п/п	Пол	Ранги вербальных способностей
1	1	1
2	0	10
3	1	6
4	1	9
5	0	15
6	1	7
7	0	8
8	0	13
9	1	4
10	1	3
11	1	5
12	0	11
13	1	12
14	1	2
15	0	14

237

В данном случае правильность ранжирования можно не про­верять, поскольку нет совпадающих рангов и ранжирование про­водится по порядку.

В таблице 11.11 юноши обозначены кодом 1, а девушки 0. В нашем случае юношей 9 человек, а девушек 6.

Прежде чем произвести расчет по формуле (11.17), найдем необходимые величины т.е. средние значения рангов отдельно для юношей и для девушек.

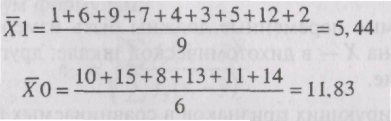
Вычисляем R_3Mnrt> по формуле (11.17):

Проверим значимость полученного коэффициента корреля­ции с помощью формулы (11.9); при k = п-1- 15-2= 13:

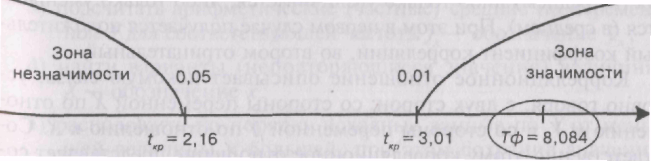
Число степеней свободы в нашем случае будет равно k = 13. По таблице 16 Приложения 1 для k = 13 находим критические значения критерия Стьюдента, они равны соответственно для Р < 0,05 t_кр= 2,16 и для Р< 0,01 t_кр = 3,01. В принятой форме

записи это выглядит так:

Строим «ось значимости»:

238

Результат попал в зону значимости. Поэтому принимается ги­потеза Н1, согласно которой полученный рангово-бисериальный коэффициент корреляции значимо отличается от нуля. Иными словами, на данной выборке подростков обнаружены значимые тендерные различия по степени выраженности вербальных спо­собностей.

Для применения рангово-бисериального коэффициента корре­ляции необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть измерены в разных; шкалах: одна X — в дихотомической шкале; другая Y — в ран­говой шкале.

2. Число варьирующих признаков в сравниваемых переменных X и Кдолжно быть одинаковым.

3. Для оценки уровня достоверности рангово-бисериального ко-

эффициента корреляции следует пользоваться формулой (11.9) и таблицей критических значений для t-критерия Стьюдента I при k = п - 2.