11.5.1. Второй способ вычисления коэффициента «φ»

Коэффициент «ф» можно вычислить, не применяя метод кодирования. В этом случае используется так называемая четы-рехпольная таблица, или таблица сопряженности. Каждую клетку таблицы обозначим соответствующими буквами a, b, и d. Используя эту таблицу, решим задачу 11.5, приведенную в предыдущем разделе. Представим данные этой задачи в виде таблицы 11.7.

227

Таблица 11.7

Значение признаков	Семейное положение		Сумма
	Холостые	Женатые
Плохо учится	а = 2	Ь = 4	6
Учится хорошо	с = 5	d = 1	6
Сумма	7	5	12

В каждой клетке таблицы 11.7 приведено число студентов, обладающих сразу двумя характеристиками. Например в верхней левой клетке, имеющей обозначение а, указано общее число студентов, которые одновременно являются холостыми и име­ют плохую успеваемость. Подобных студентов было обнаружено 2 человека. Таким же способом заполняют все клетки таблицы.

Приведем общую формулу расчета коэффициента «φ» по таб­лице сопряженности:

(11.11)

Подставляем данные таблицы 11.7 в формулу 11.11, полу­чаем:

Значение φ_эмп , как этого следовало ожидать, получилось то же самое, что и в предыдущем случае. Поскольку мы уже оцени­ли уровень значимости, второй раз этого делать не стоит.

Для применения коэффициента корреляции «ф» необходимо соблюдать следующие условия:

1- Сравниваемые признаки должны быть измерены в дихотоми­ческой шкале.

2. Число варьирующих признаков в сравниваемых переменных X и /должно быть одинаковым.

3, Для оценки уровня достоверности коэффициента «φ» следует пользоваться формулой (11.9) и таблицей критических значе­ний для t-критерия Стьюдента при k= n - 2.

228

11.6. Коэффициент корреляции «τ» Кендалла

Коэффициент корреляции «τ» (тау) Кендалла относится к числу непараметрических, т.е. при вычислении этого коэффици­ента не играет роли характер распределения сравниваемых пере­менных. Коэффициент «τ» предназначен для работы с данными, полученными в ранговой шкале. Иногда этот коэффициент мож­но использовать вместо коэффициента корреляции Спирмена, поскольку способ его вычисления более прост. Он основан на вычислении суммы инверсий и совпадений.

Решим следующую задачу, применяя коэффициент «т».

3 а д а ч а 11.6 Психолог просит супругов проранжировать семь личностных черт, имеющих определяющее значе­ние для семейного благополучия. Задача заключа­ется в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам.

Данные задачи и необходимые для вычисле­ний коэффициента Кендалла столбцы предста-вим сразу в виде таблицы 11.8:

Таблица 118

Черты личности	Муж	Жена	Совпадения	Инверсии
Ответственность	7	1
Общительность	1	5
Сдержанность	3	7
Выносливость	2	6
Жизнерадостность	5	4
Терпеливость	4	3
Решительность	6	2
Сумма

Для подсчета коэффициента корреляции «т» (тау) необходи-мо упорядочить второй столбец (оценки мужа) таблицы 11.8 по возрастанию рангов, в нашем случае от 1 до 7. Соответственно

229

этому поменяются местами как сами черты, так и соответствую­щие ранги третьего ряда. Оформим эти преобразования в новую таблицу 11.9:

Таблица 11.9

№ 1	№2	№3	№4	№ 5
Черты личности	Муж	Жена	Совпадения	Инверсии
Общительность	1	5	2	4
Выносливость	2	6	1	4
Сдержанность	3	7	0	4
Терпеливость	4	3	1	2
Жизнерадостность	5	4	0	2
Отзывчивость	6	2	0	1
Ответственность	7	1	0	0
Сумма			4	17

Посмотрим, как следует заполнять последние два столбца таб­лицы 11.9. Теперь для работы нам нужен только столбец с ранга­ми, проставленными женой. На его основе заполним последние два столбца таблицы 11.9, подсчитав, сначала число совпадений.

Подсчет совпадений происходит следующим образом: берем са­мое верхнее число третьего столбца — 5. Подсчитываем сколько всего чисел больших 5 встречаются ниже в этом же столбце. Нахо­дим их — это 6 и 7. Их всего два. Двойку ставим напротив числа 5 в колонке «Совпадения». Берем затем следующее число 6 — ниже по столбцу и больше его, также ниже по столбцу, встречается только одно число 7. Ставим напротив 6 в столбце «Совпадения» — 1. Бе­рем следующее число 7 — больше по величине не может встре­титься ни одно число, поскольку 7 это максимальный ранг. Ста­вим напротив 7 в столбце «Совпадения» — 0. И так далее.

Для определения количества инверсий опять берем самое вер­хнее число третьего столбца — 5. Подсчитываем, сколько всего чисел встречаются ниже по столбцу, меньших чем 5. Это числа 4, 3, 2 и 1. Их 4. Ставим напротив числа 5 в столбце «Инверсия» чис­ло 4. Берем следующее число 6 — ниже по столбцу и меньше, чем 6, встречаются те же числа, что и для 5. Ставим напротив 6 в

230

столбце «Инверсия» число — 4. То же верно и для числа 7. Мень­ше числа 3 ниже по столбцу встречаются числа 2 и 1. Ставим на­против 3 в столбце «Инверсия» число — 2. И так далее.

Число совпадений обозначается буквой Р, а число инверсий буквой Q. Для проверки правильности подсчета числа инверсий и совпадений используется следующая формула:

(11.12)

Где Р — число совпадений,

Q — число инверсий,

N — число ранжируемых признаков (черт). Подставляем в формулу (11.12) полученные в нашем случае величины, получаем:

Следовательно, подсчет числа инверсий и совпадений был произведен правильно.

Подсчет коэффициента Кендалла может осуществляться по трем тождественным формулам. Первая формула:

(11.13) В двух других формулах используются либо Р, либо Q:

(11.14)

(11.15)

Проведем подсчет коэффициента корреляции по всем трем формулам:

(11.13) (11.14)

231

(11.15)

Проверим уровень значимости коэффициента корреляции по формуле (11.9):

Число степеней свободы в нашем случае будет k = п - 2 = = 7-2 = 5. По таблице 16 Приложения 1 для k = 5 находим кри­тические значения критерия Стьюдента, они равны соответ­ственно для Р< 0,05 t_кр = 2,57 и для Р< 0,01 г = 4,03. В принятой форме записи это выглядит так:

Строим «ось значимости»:

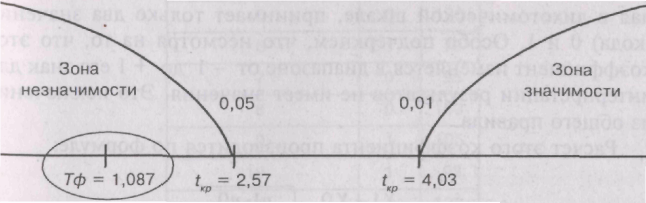
Значение величины Тф попало в зону незначимости. В терми­нах статистических гипотез гипотеза Н₁ отклоняется и принима­ется гипотеза Н₀ о том, что коэффициент корреляции «τ» Кен-далла достоверно не отличается от нуля. Иными словами, согла­сованности между мужем и женой в оценке значимых для семей­ного благополучия личностных черт нет.

Для применения коэффициента корреляции «т» Кендалла необ­ходимо соблюдать следующие условия:

1. Сравниваемые признаки должны быть измерены в порядковой шкале.

232

2. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.

3. Величина «τ» Кендалла независима от закона распределения величин Х и Y.

4. При расчетах этого коэффициента не допускается использова­ние одинаковых рангов.

5. Для оценки уровня достоверности коэффициента «т» следует пользоваться формулой (11.9) и таблицей критических значе­ний для t-критерия Стьюдента при k = п - 2.